今天在学习力扣上94题二叉树的中序遍历时,js的实现方法之一是递归,但是函数内递归是双重,花了一些时间来理解双重递归调用的执行顺序。
先看如下例子,参考文章(双递归的执行过程理解)
示例代码如下:
const fn = (n) => {
if (n > 0) {
console.log('n1====', n)
fn(n - 1)
console.log('n2====', n)
fn(n - 2)
console.log('n3====', n)
}
}
fn(3)
我们可以先考虑一下输出的结果是什么呢?
答案揭晓如下:
// n1==== 3
// n1==== 2
// n1==== 1
// n2==== 1
// n3==== 1
// n2==== 2
// n3==== 2
// n2==== 3
// n1==== 1
// n2==== 1
// n3==== 1
// n3==== 3
一开始看到这个结果,真是两眼一黑,什么鬼!那我们先不急,一步步来分析~
1、首先注意第一次递归调用:首次调用时,n=3,所以输出结果n1 = 3是毫无疑问的,接着执行fn(n - 1),因为n - 1 = 2 > 0,所以执行第一次递归没问题吧
2、接着就是一个知识点:进栈
众所周知,js是单线程,fn函数内均为同步执行,所以第一次递归之后,n=3进栈,执行fn(n - 1)的n=2操作,而我把fn(n - 1)执行的过程称为进栈(压栈)。如下图:

3是最先进栈,所以在栈底。
注意:此时fn(n - 1)以下的代码片段全部未执行。
输出结果为:
n1==== 3
n1==== 2
n1==== 1
当n = 1时,执行fn(n - 1),则n = 0,即if (n > 0)失效。当前递归结束,开始释放栈内存(出栈),而栈是后进先出结构,如下图:
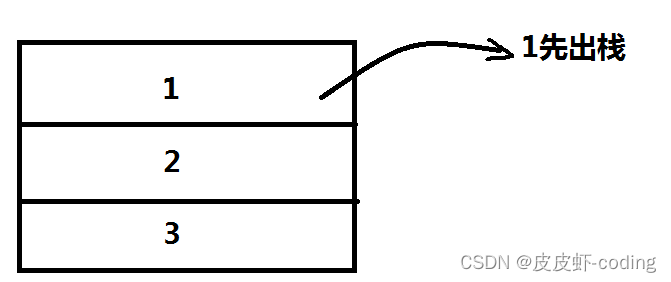
3、接上图,n=1 出栈,同步执行以下代码片段
console.log('n2====', n)
fn(n - 2)
console.log('n3====', n)
所以第四行打印出 n2==== 1
接着执行fn(n - 2),因当前n=1,不符合表达式n>0情况,所以本次递归调用不执行。
接着输出打印 n3==== 1,此时到输出的打印结果第五行。
4、n=1 出栈后,2出栈:
重复上一步,输出:
n2==== 2
n3==== 2
此时到打印结果第7行。
5、n=2 出栈后,3出栈:
输出结果n2==== 3后
执行递归fn(n - 2),此时 if 表达式 n = 1 > 0 成立,则从头执行。
(注意:此时n = 3进栈,最后一行代码console.log('n3====', n)不执行)
执行fn(3 - 2)后:
首先输出n1==== 1,再执行fn(n - 1),表达式不成立,接着向下执行,
输出n2==== 1,向下执行fn(n - 2),表达式不成立,准备出栈,继续向下执行,
输出n3==== 1
最后!注意:之前执行fn(n - 2)时有n = 3进栈!所以此时同步流程结束,需要出栈:
输出最后一个结果n3==== 3
至此,双递归调用流程结束。
// =================================
到这,终于明白双递归是怎么被调用执行的了!~
接下来,我们来看怎么用递归的方式实现二叉树中序遍历:
中序遍历返回顺序是左 => 根/中 => 右,如下图:
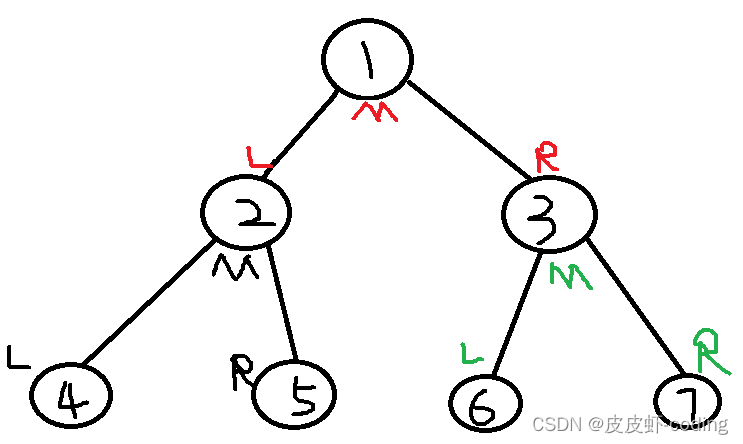
按照中序遍历输出的结果应该是 [4, 2, 5, 1, 6, 3, 7]。
依照上面例子给我们的经验,要获取左子树的最后一个左节点的值再进行操作,那我们可以进行压栈,当左子树的某个左节点left为null时,代表当前节点为最后节点,数据结构大致如下:
const tree = {
val: '1',
left: {
val: '2',
left: { val: '4', left: null, right: null },
right: { val: '5', left: null, right: null }
},
right: {
val: '3',
left: { val: '6', left: null, right: null },
right: { val: '7', left: null, right: null }
},
}
代码实现如下:
var inorderTraversal = function (root) {
let arr = []
const fn = (tree) => {
if (!tree) return
fn(tree.left)
arr.push(tree.val)
fn(tree.right)
}
fn(root)
return arr
};
console.log(inorderTraversal(tree))
如上,执行fn(tree.left)时,一直在压栈,一直到 { val: '4', left: null, right: null },这一层,执行结束,释放栈,此时栈如下(看val值):
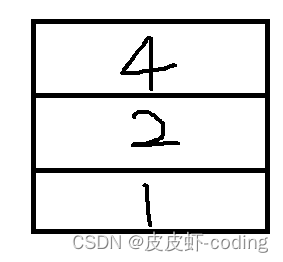
4首先出栈,执行arr.push(tree.val)后,执行递归fn(tree.right),val=4的这一层,right = null,被return,本次执行结束。
2再次出栈,再执行递归fn(tree.right),成立,arr此时为[4, 2, 5].
1出栈,执行后,arr = [4, 2, 5, 1],
再遍历右子树,以此类推。
中序遍历完成。









