原文链接:https://time.geekbang.org/column/intro/100017301
27 | 递归树:如何借助树来求解递归算法的时间复杂度?
如何借助树来分析归并排序算法的时间复杂度?
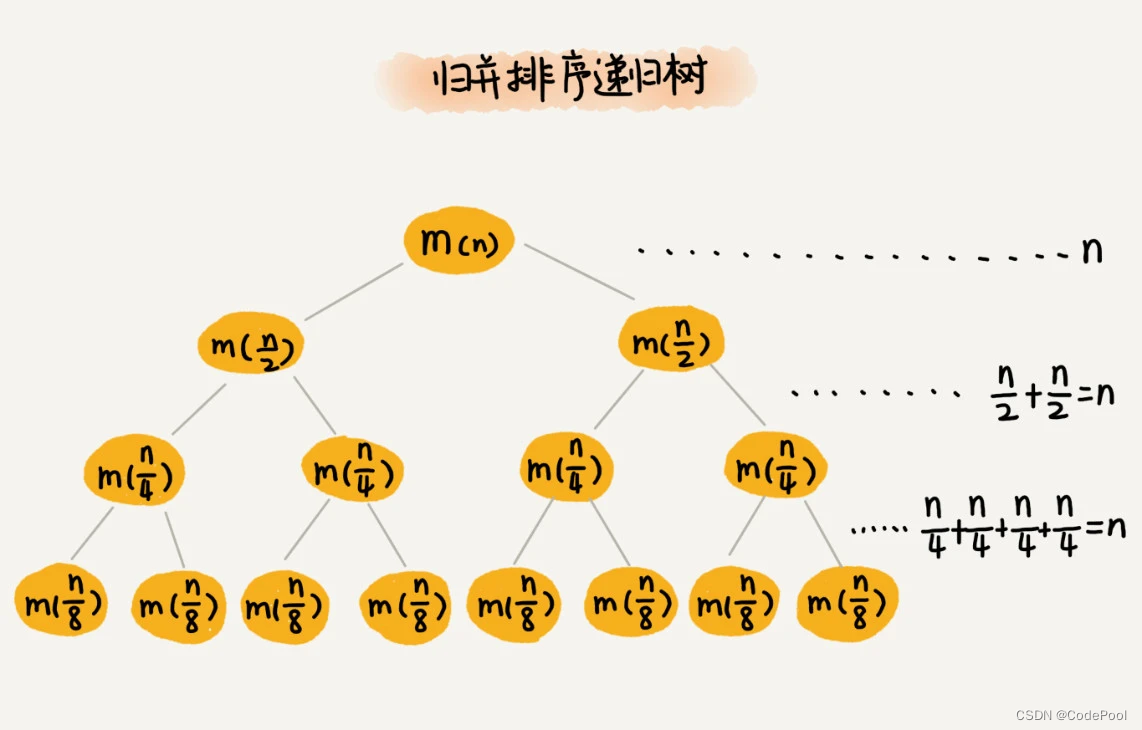
每次分解一分为二,代价很低,时间上消耗记作O(1)。
每一层合并消耗时间相同,和数据规模相关,记作 O(n)。
归并排序递归树是一颗满二叉树,高度为 log2n。
归并排序时间复杂度:O(n logn)。
如何借助树来分析快速排序算法的时间复杂度?
平均情况:1 : k
k = 9 时。
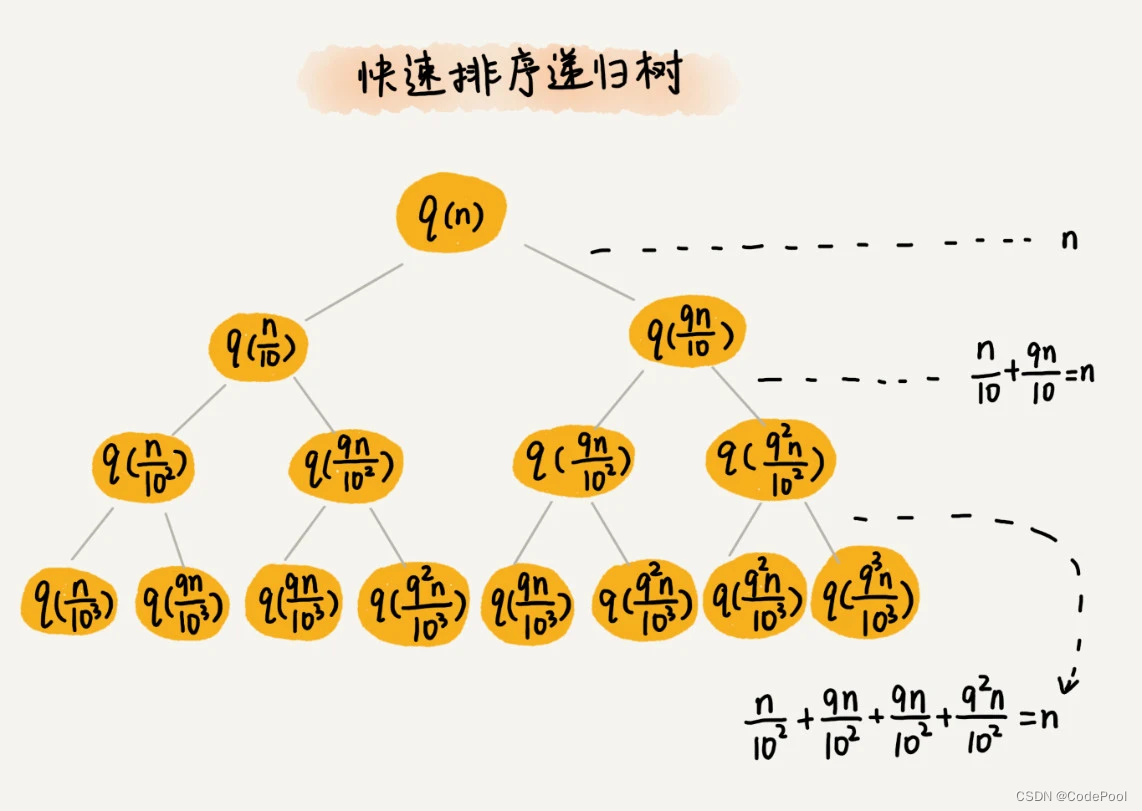
每一层遍历 n 个元素。
快速排序结束条件:叶子节点 1 个元素。
根节点 n 个元素到叶子节点 1 个元素最短路径每一层乘 1 /10,最长路径每一层乘 9 / 10。
根节点到叶子节点最短路径:log10n,最长路径 log(10 / 9 ) n。
遍历个数在 n * log10 到 n * log(10 / 9 ) n 之间,快速排序时间复杂度为:O(n logn)。
k 的值不随 n 改变,对最终时间复杂度无影响。
如何借助递归树来分析斐波那契数列的时间复杂度?
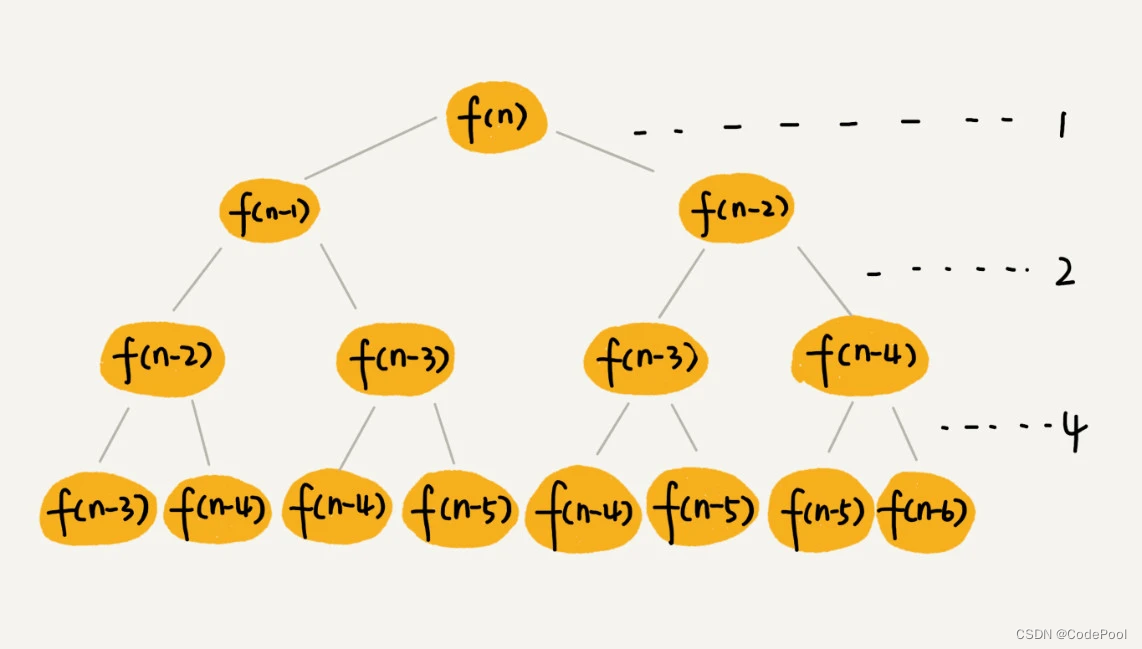
f(n) 分解为 f(n - 1) 和 f(n - 2),每次数据规模 -1 或 -2,叶子节点数据规模是 1 或者 2。
根节点到叶子节点最长为 n ,最短为 n / 2。
合并的操作只需要一次加法运算,耗时记作 O(1)。
每一层消耗时间为 2^ (k - 1) ,路径长度为 n 总和为 2^n - 1。
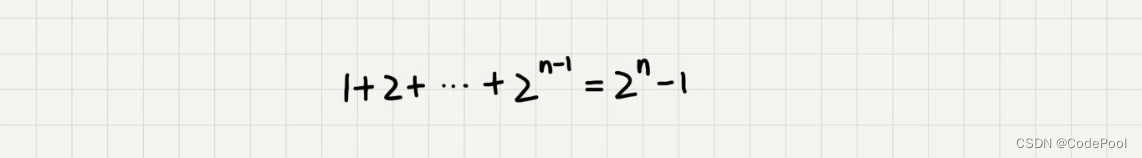
路径长度为 n 总和为 2^(n / 2) - 1。
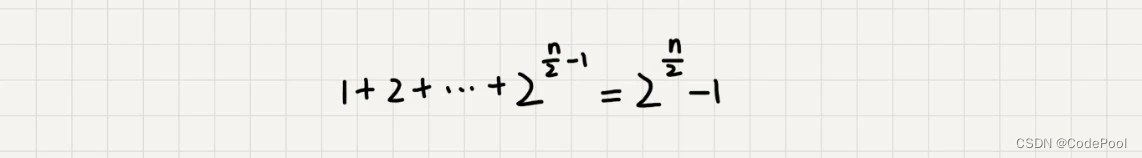
时间复杂度为指数级别。
如何借助递归树来分析全排列的时间复杂度?
最后一位有 n 种情况,求解 n 个 “n - 1数据的排列” 的子问题。
递推公式:
假设数组中存储的是1,2, 3...n。
f(1,2,...n) = {最后一位是1, f(n-1)} + {最后一位是2, f(n-1)} +...+{最后一位是n, f(n-1)}。
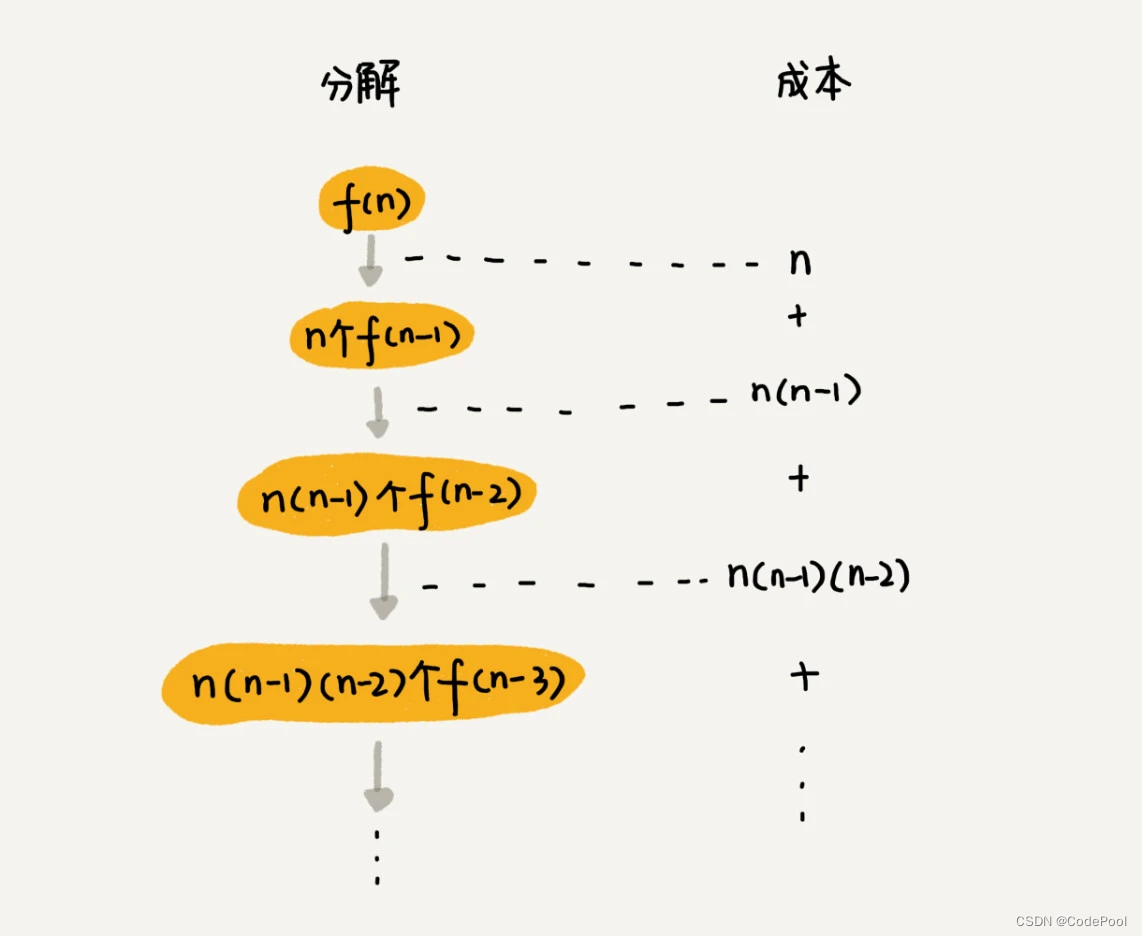
第一层有 n 此交换,第二层有 n (n - 1) 次交换,第三层有 n(n - 1)(n - 2) 此交换,最后一层有 n(n - 1)(n - 2) *…21 次交换。
总交换次数:
n + n*(n-1) + n*(n-1)*(n-2) +... + n*(n-1)*(n-2)*...*2*1
n*(n-1)*(n-2)*...*2*1 为 n!
总和小于 n * n!,全排列递归时间复杂度大于O(n!),小于O(n * n!)。时间复杂度非常高。
1 个细胞的生命周期是 3 小时,1 小时分裂一次。求 n 小时后,容器内有多少细胞?如何分析递归时间时间复杂度?
需要重新系统完整的分析。
28 | 堆和堆排序:为什么说堆排序没有快速排序快?
特殊的树:堆(Heap)。
堆排序:原地排序,时间复杂度为O(n logn)。
如何理解 “堆”?
堆满足的条件是什么?(2个)
- 堆是一个完全二叉树。(除了最后一层,其他层节点个数都是满的,最后一层的节点都靠左排列。)
- 堆中每个节点的值都大于等于[大顶堆](或小于等于[小顶堆])其左右子节点的值。
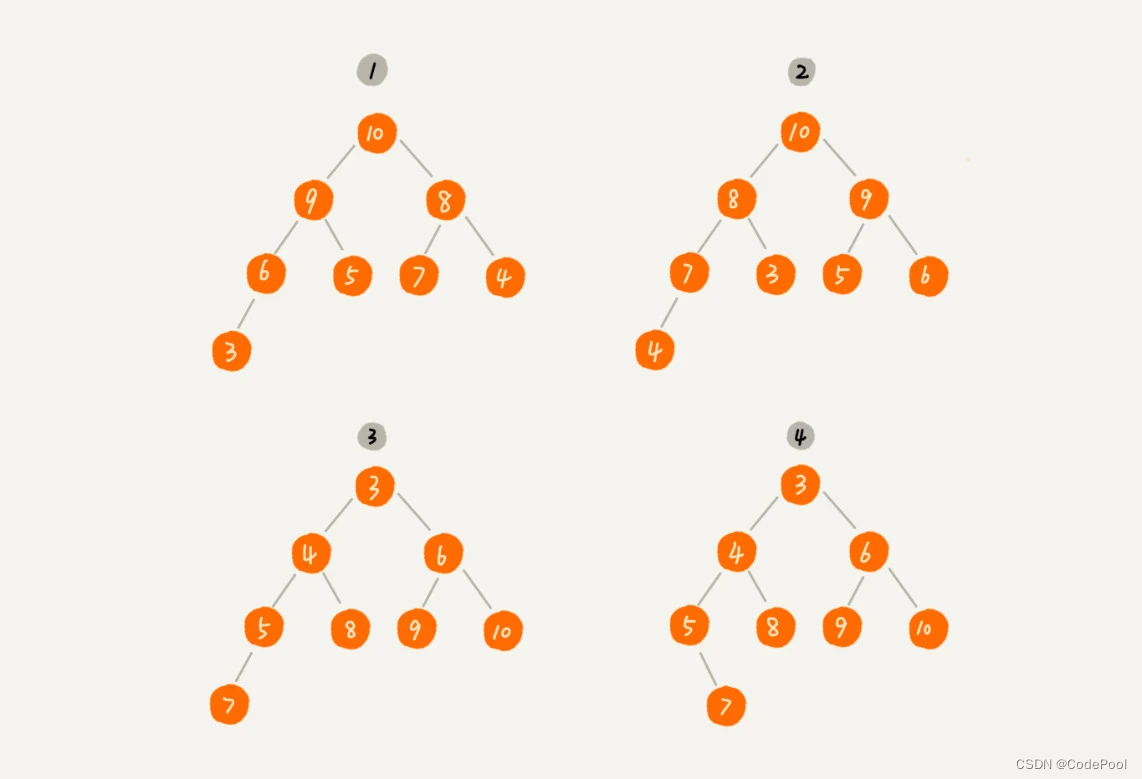
1 和 2是大顶堆,3是小顶堆,4不是堆。
如何实现一个堆?
如何存储一个堆?
完全二叉树用数组存储。
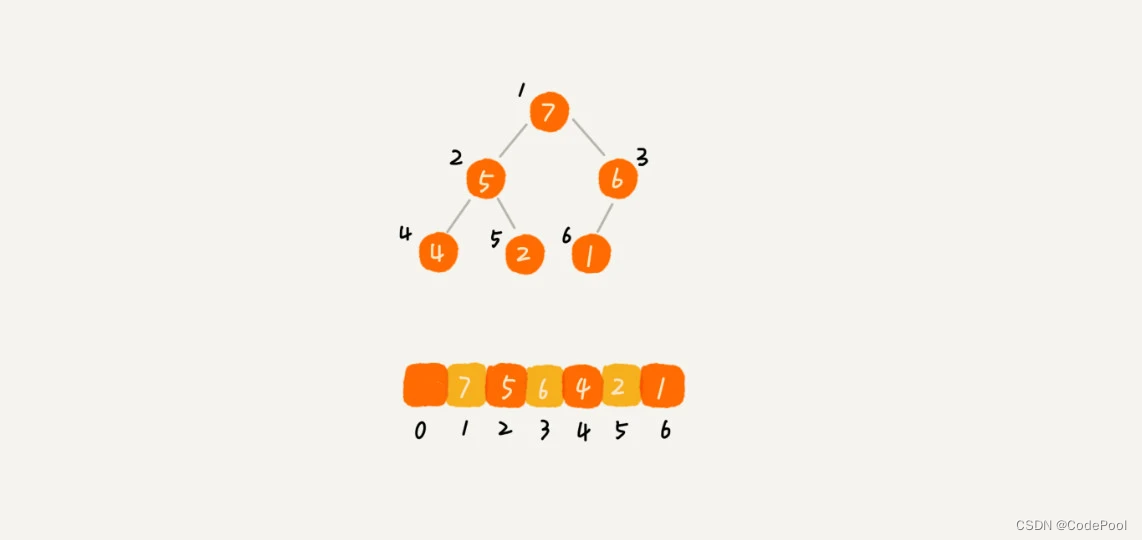
下标为 i 的左子节点下标为 i * 2,右子节点下标为 i * 2 + 1,父节点为下标 i / 2 的节点。
堆支持哪些操作?
插入元素
往堆中插入一个元素,满足堆的特性,通过堆化实现。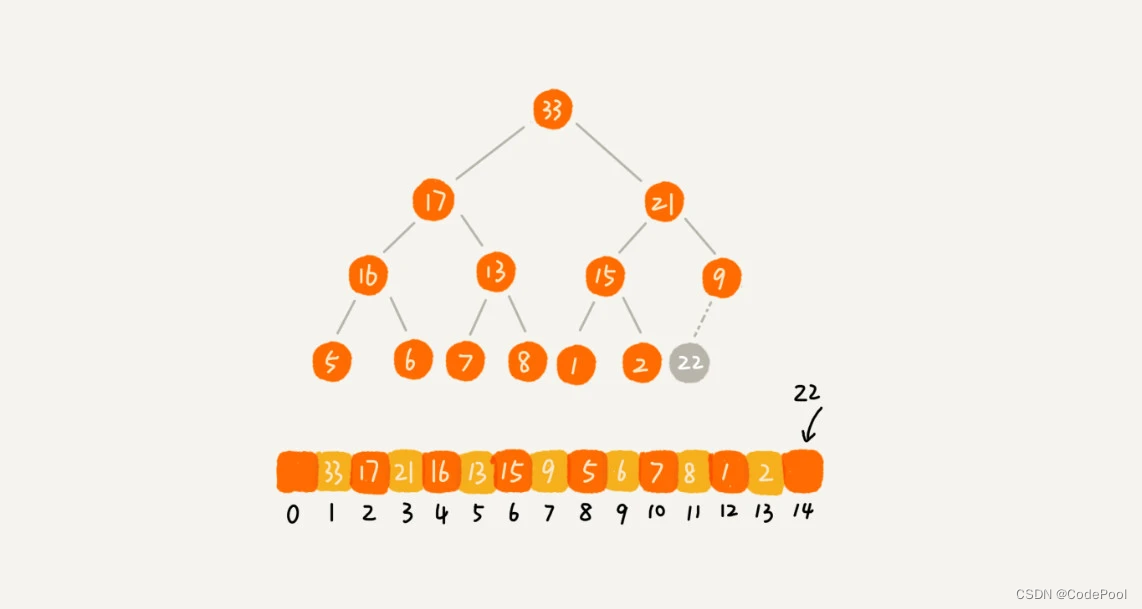
从下往上堆化:顺着节点所在的路径,向上或者向下,对比,然后交换。
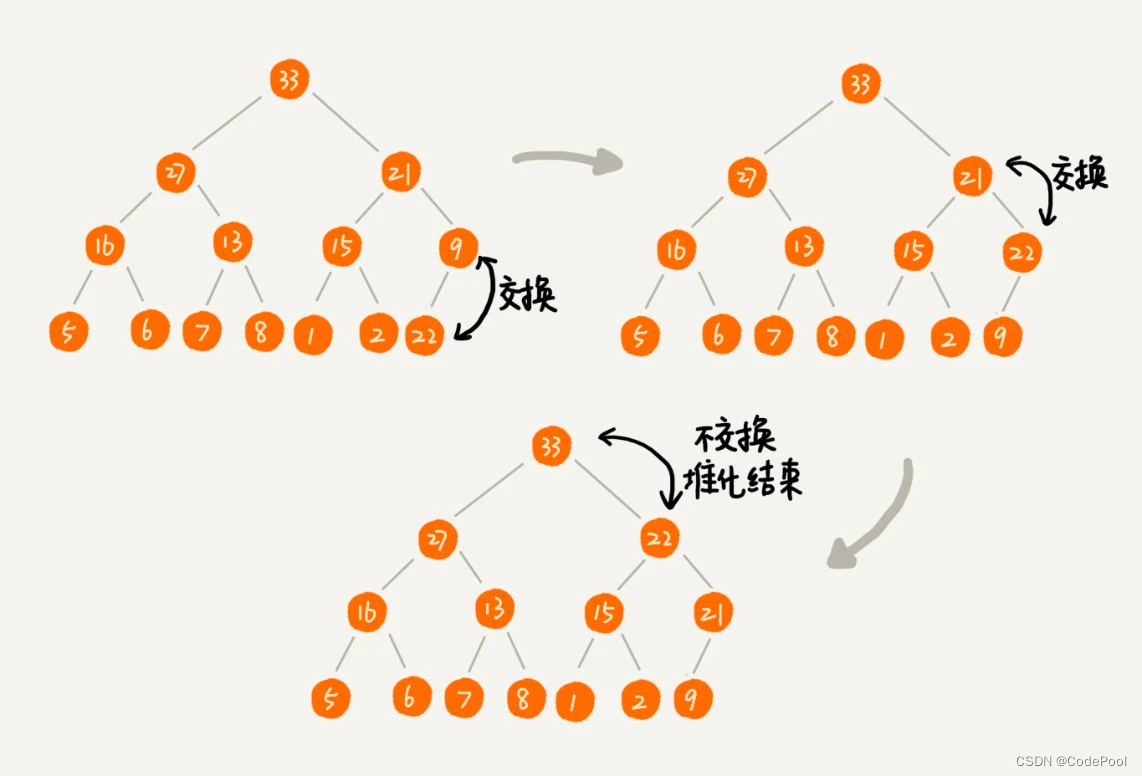
堆化的代码实现过程:
public class Heap {
private int[] a; // 数组,从下标1开始存储数据
private int n; // 堆可以存储的最大数据个数
private int count; // 堆中已经存储的数据个数
public Heap(int capacity) {
a = new int[capacity + 1];
n = capacity;
count = 0;
}
public void insert(int data) {
if (count >= n) return; // 堆满了
++count;
a[count] = data;
int i = count;
while (i/2 > 0 && a[i] > a[i/2]) { // 自下往上堆化
swap(a, i, i/2); // swap()函数作用:交换下标为i和i/2的两个元素
i = i/2;
}
}
}
删除堆顶元素
把最后一个节点放在堆顶,父子节点对比,不满足父子节点大小关系的,互换两个节点。重复该过程,知道父子节点之间满足大小关系为止。
移除的是数组中最后一个元素,堆化的过程都是数据交换操作,不会出现数组空洞。
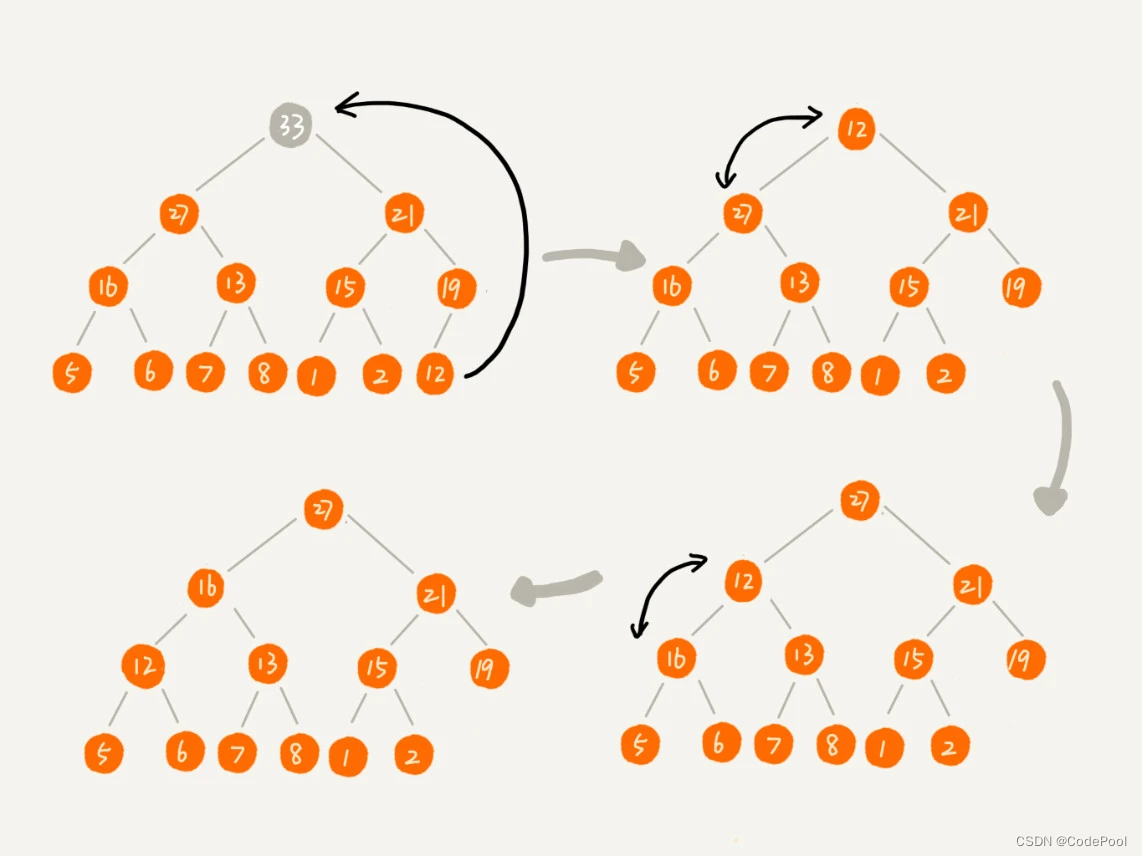
代码演示:
public void removeMax() {
if (count == 0) return -1; // 堆中没有数据
a[1] = a[count];
--count;
heapify(a, count, 1);
}
private void heapify(int[] a, int n, int i) { // 自上往下堆化
while (true) {
int maxPos = i;
if (i*2 <= n && a[i] < a[i*2]) maxPos = i*2;
if (i*2+1 <= n && a[maxPos] < a[i*2+1]) maxPos = i*2+1;
if (maxPos == i) break;
swap(a, i, maxPos);
i = maxPos;
}
}
n 个节点的完全二叉树,树高度不会超过 log2n。
堆化时间复杂度和树高度成正比,为O(log n)。
插入元素和删除堆顶元素主要逻辑是堆化,时间复杂度为O(log n)。
如何基于堆实现排序?
时间复杂度稳定为 O(n logn),原地排序算法。
建堆
第一种:在堆中插入一个元素的思路。从前往后处理数组,从下往上堆化。
第二种:从后往前处理数组,每个数据都从上往下堆化。
叶子节点往下堆化只能自己和自己比较,所以从最后一个非叶子节点开始堆化:
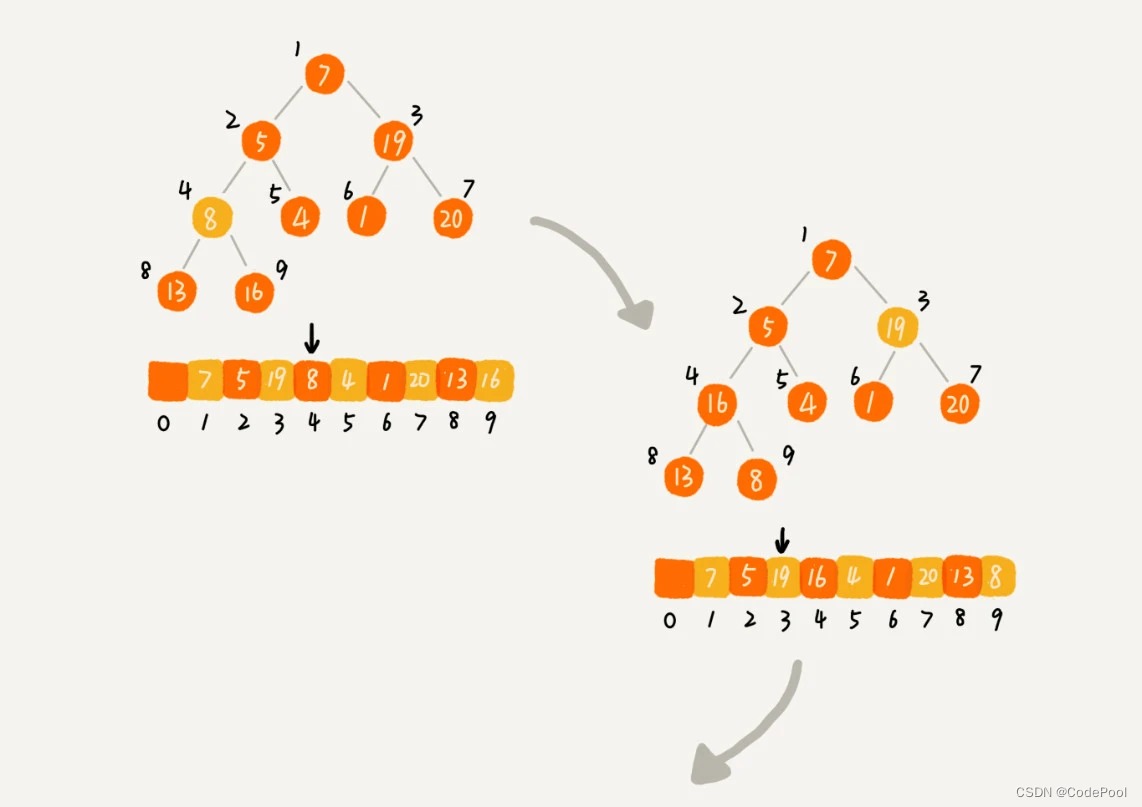
private static void buildHeap(int[] a, int n) {
for (int i = n/2; i >= 1; --i) {
heapify(a, n, i);
}
}
private static void heapify(int[] a, int n, int i) {
while (true) {
int maxPos = i;
if (i*2 <= n && a[i] < a[i*2]) maxPos = i*2;
if (i*2+1 <= n && a[maxPos] < a[i*2+1]) maxPos = i*2+1;
if (maxPos == i) break;
swap(a, i, maxPos);
i = maxPos;
}
}
建堆的时间复杂度:
叶子节点不需要堆化,需要堆化的节点从倒数第二层开始。每个节点的堆化过程,比较和交换的节点个数,根节点的高度 k 成正比。
每一层节点个数和对应的高度换出来如下:
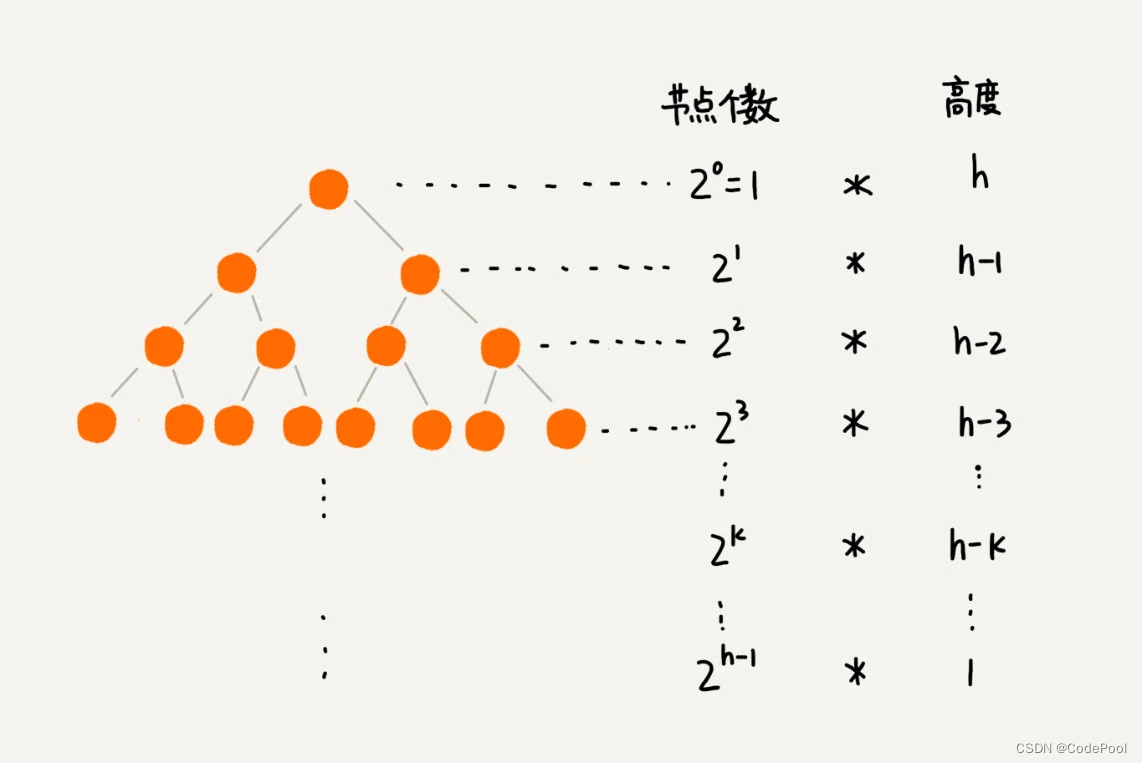
将每个节点的高度求和,得出的就是建堆的时间复杂度。
每个非叶子节点高度求和:
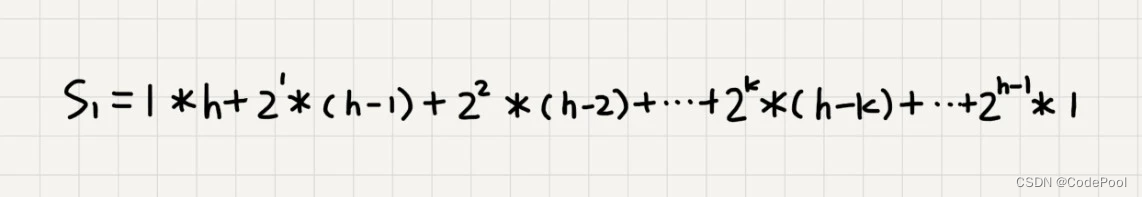
把公式左右都乘以 2,就得到另一个公式 S2。我们将 S2 错位对齐,并且用 S2 减去 S1,可以得到 S

通过等比数列求和公式:
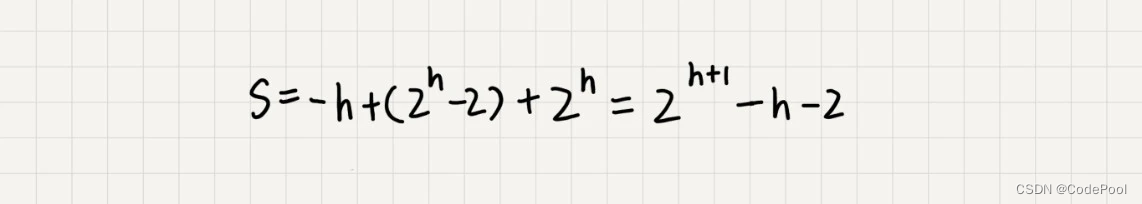
h = log2你,带入公式,S = O(n),建堆时间复杂度为O(n)。
排序
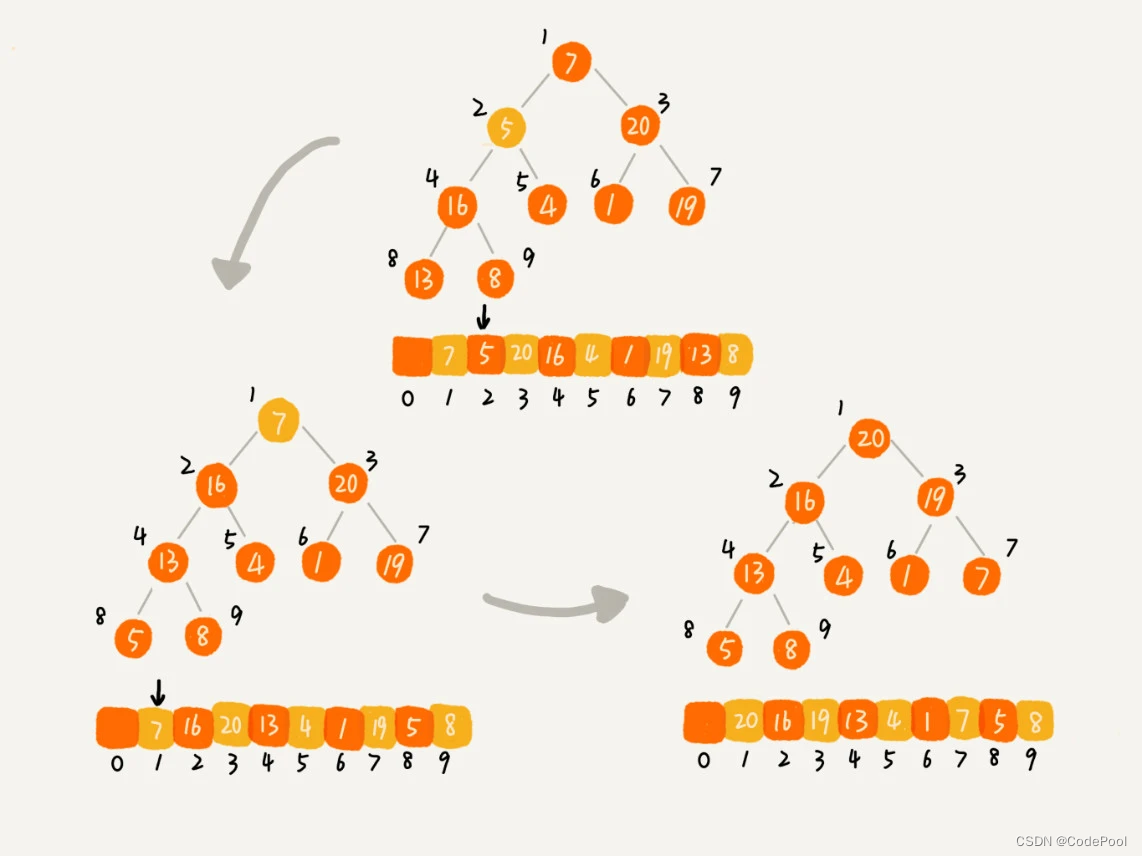
数组中第一个元素,堆顶最大元素和最后一个元素交换,最大元素放到下标为 n 的位置。
将 n - 1 个元素重新构建成堆,再取堆顶元素放到 n - 1 ,一直重复,最后堆中只有下标为 1 的一个元素,排序工作就完成了。
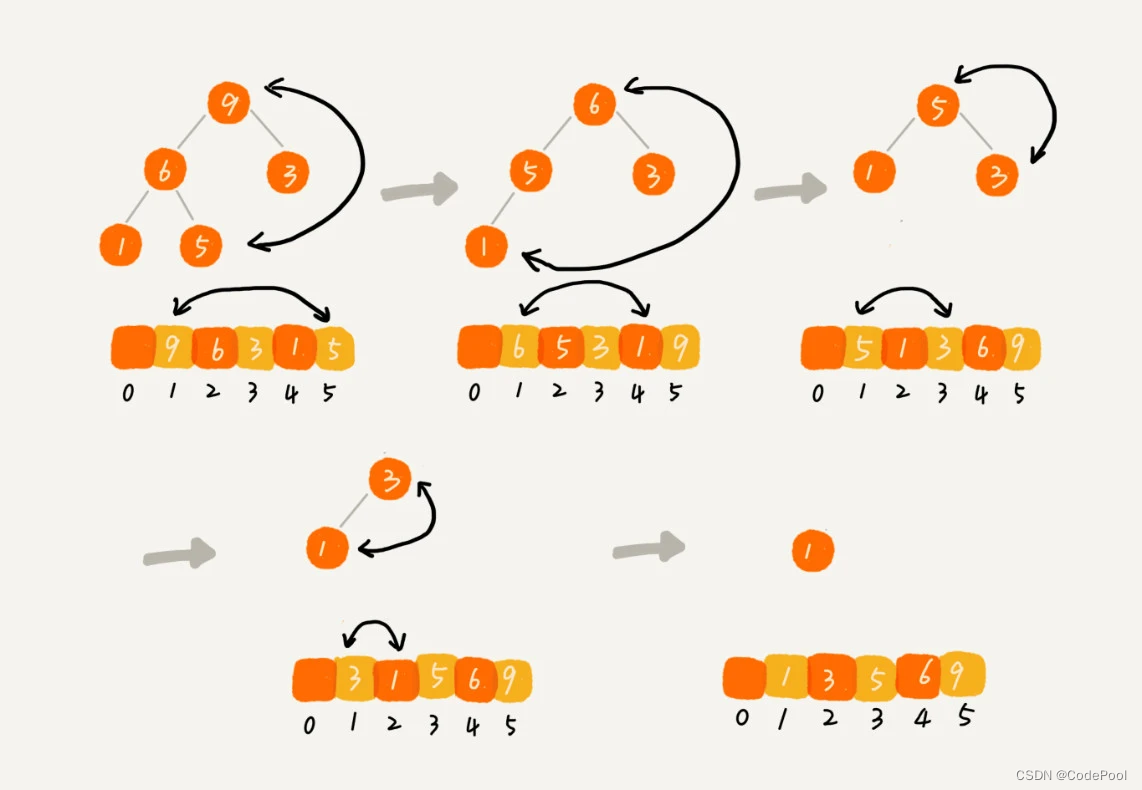
代码演示:
// n表示数据的个数,数组a中的数据从下标1到n的位置。
public static void sort(int[] a, int n) {
buildHeap(a, n);
int k = n;
while (k > 1) {
swap(a, 1, k);
--k;
heapify(a, k, 1);
}
}
原地排序。
建堆时间复杂度为 O(n),排序过程时间复杂度为O(n logn),堆整体的时间复杂度为 O(n logn)。
不稳定排序。
解答开篇
堆排序数据访问方式没有快速排序友好。
快速排序,数据顺序访问,可以有效利用CPU缓存。
堆排序,数据跳着访问。
堆顶节点堆化,会依次访问数组下标1,2,4,8。
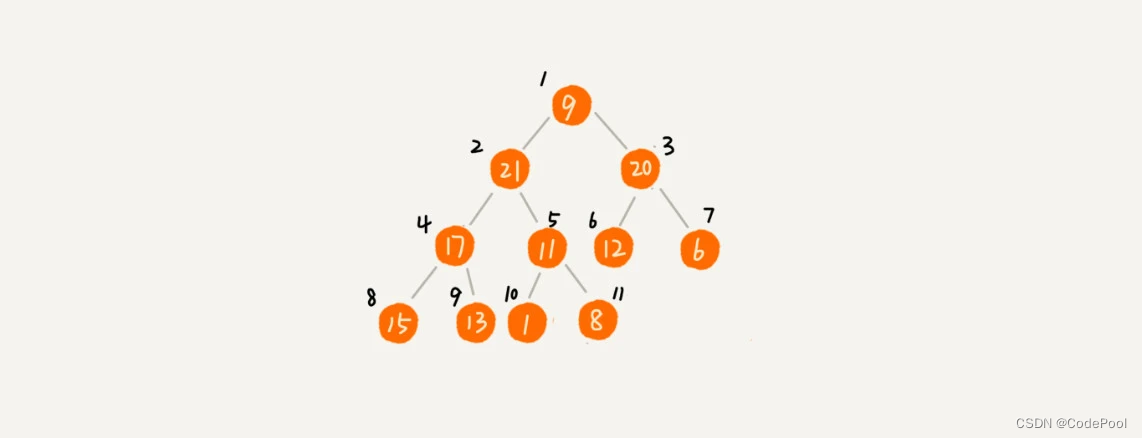
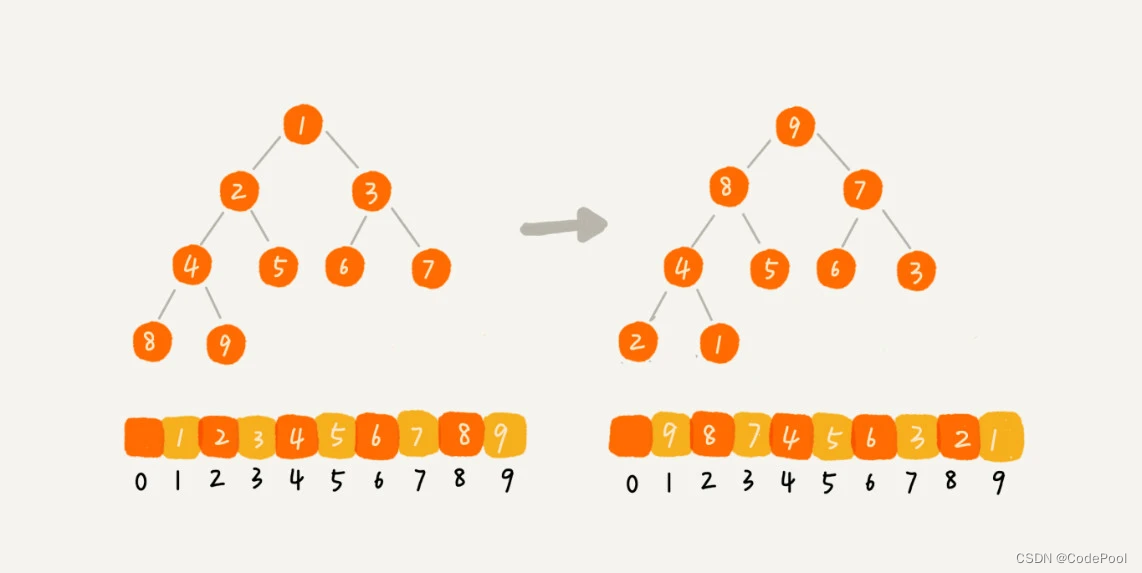
同样的数据,排序过程中,堆排序算法的数据交换次数多于快速排序。
快速排序数据交换次数不会比逆序度多。
堆排序第一步是建堆,建堆会打乱数据原有的先后顺序,导致原数据有序度降低。
内容小结
堆是一种完全二叉树。
大顶堆和小顶堆。
插入一个数据:新插入元素放到数组最后,从下往上堆化。时间复杂度:O(logn)
删除堆顶元素:将数组中最后一个元素放到堆顶,从上往下堆化。时间复杂度:O(logn)
堆排序:
建堆:将下标从 n / 2 到 1 的节点,依次从上到下堆化操作,将数组中的数据组织成堆这种数据结构。
排序:迭代的将堆顶元素放在堆末尾,将堆大小减一,然后再堆化。重复这个过程,直到堆中只剩下一个元素,整个数组中数据有序。
课后思考
对于完全二叉树来说,下标从 n / 2+1 到 n 的都是叶子节点,这个结论是怎么推导出来的呢?
关于堆,你还能想到它的其他应用吗?








