目录
一,概念和效果
记忆化搜索可以说是带备忘录的递归,实现这个算法的目的便是减少递归时对同一个节点的多次遍历从而提高学习效率。学习这个算法,理解这个算法最好的方式便是通过能够用记忆化搜索的题目来理解。
二,题目
1.斐波那契数
1.题目
斐波那契数 (通常用
F(n)表示)形成的序列称为 斐波那契数列 。该数列由0和1开始,后面的每一项数字都是前面两项数字的和。也就是:F(0) = 0,F(1) = 1 F(n) = F(n - 1) + F(n - 2),其中 n > 1给定
n,请计算F(n)。
2.题目接口
class Solution {
public:
int fib(int n) {
}
};3.解题思路
相信大家都知道如何解决斐波那契数的问题。这个问题的经典解决方式便是运用到递归解法。使用递归时要明确的便是递归的出口。斐波那契数的递归出口便是在n == 0或者n==1时。这两个条件下的返回值便是它们本身。当n不等于0和1时f(n) = f(n-1)+f(n-2)条件成立。
根据以上思路便可以写出如下解题代码:
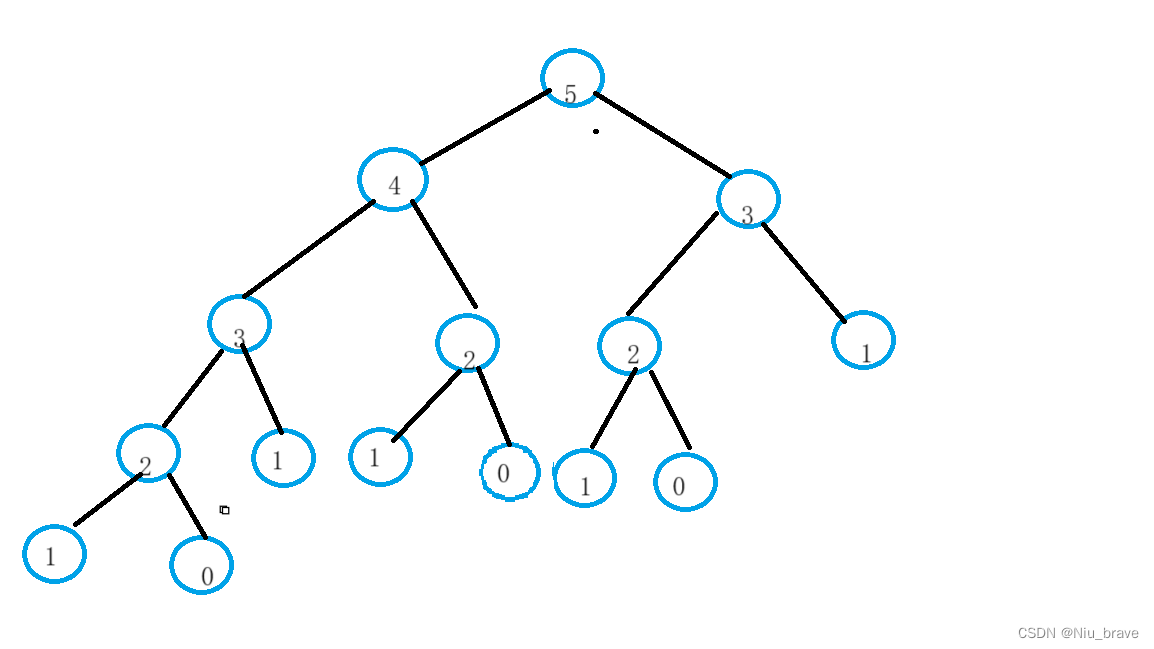
class Solution { public: int fib(int n) { return dfs(n); } int dfs(int n) { if(n == 0||n == 1) { return n; } return dfs(n-1)+dfs(n-2); } };但是我们都知道在递归时会有大量的重复计算。比如当n == 5时递归展开图如下:
在这里可以看到2这个节点被求了很多次,这样子便是很大的浪费了。这个时候为了提高效率便可以采用记忆化搜索的方式。记忆化搜索的实现其实也非常的简单,也就是当我们得到一个结果时便将其记录下来。当我们想要再次遍历相同的节点时只要看前面是否有记录过,若记录过便不再访问直接返回之前记录过的结果就行了。比如斐波那契数列这道题的记忆化搜索方式的解题代码如下:
class Solution { public: vector<int>memo;//表示备忘录 int fib(int n) { memo = vector<int>(n+1);//初始化 return dfs(n); } int dfs(int n) { if(n == 0||n == 1) { return n; } if(memo[n]!=0)//册中已求便无需再求 { return memo[n]; } memo[n] = dfs(n-1)+dfs(n-2);//记录在册 return memo[n]; } };
2.不同的路径
1.题目
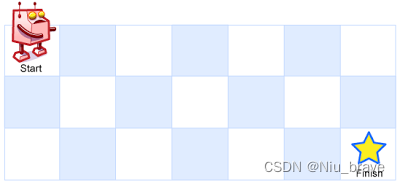
一个机器人位于一个
m x n网格的左上角 (起始点在下图中标记为 “Start” )。机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
问总共有多少条不同的路径?
2.题目接口
class Solution {
public:
int uniquePaths(int m, int n) {
}
};3.解题思路
因为机器人只能向前或者向下走,所以要到达finish位置的话首先就要到达finish的上面和左边这两个位置:
要到达这两个位置的话便又要到达这两个位置的上面和下面位置。以次类推得到公式:
f(finishi,finishj) = f(finishi-1,finishj)+f(finishi,finishj-1)。得到这个关系我们便可以知道这道题和斐波那契数列有的一拼,所以自然就会想到递归的解法。在这里便要寻找递归条件了。
1.因为目中给的m与n表示的是网格的长与宽。所以当m == 1&&n == 1时就意味着网格里面只有一个格子,也就是机器人就在右下角的格子了所以返回1。
2.当给的m与n中有一个为0的话,也就是网格的长或者宽为0,也就表示没有格子于是返回0。
根据以上分析写出代码如下:
class Solution { public: int uniquePaths(int m, int n) { return dfs(m,n); } int dfs(int m,int n) { if(m == 1&&n==1) { return 1; } if(m ==0||n==0) { return 0; } return dfs(m-1,n)+dfs(m,n-1); } };
但是这个代码会超时,所以我们得优化这个代码让这个代码变得更快。优化的方式便是记忆化搜索:
class Solution { public: vector<vector<int>>memo; int uniquePaths(int m, int n) { memo = vector<vector<int>>(m+1,vector<int>(n+1)); return dfs(m,n); } int dfs(int m,int n) { if(memo[m][n]!=0) { return memo[m][n]; } if(m == 1&&n==1) { return 1; } if(m ==0||n==0) { return 0; } memo[m][n] = dfs(m-1,n)+dfs(m,n-1); return memo[m][n]; } };
可以看到这道题的记忆化搜索处理方式和上一道题一毛一样。
3.最长增长子序列
1.题目
给你一个整数数组
nums,找到其中最长严格递增子序列的长度。子序列 是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,
[3,6,2,7]是数组[0,3,1,6,2,2,7]的子序列。
2.题目接口
class Solution {
public:
int lengthOfLIS(vector<int>& nums) {
}
};3.解题思路
这道题的解题思路其实也不太难,就是要遍历一下每一个下标然后求出以每一个下标的起点为开始位置的子序列长度。但是因为我们要求的是最大长度所以需要比较更新最大长度。以这个思路写成代码如下:
class Solution { public: int len; int lengthOfLIS(vector<int>& nums) { len = nums.size(); int ret = 0; for(int i = 0;i<len;i++) { ret = max(ret,dfs(i,nums));//得到以某个下标为起点的最大长度 } return ret; } int dfs(int i,vector<int>&nums) { int ret = 1;//每一个子序列的最小长度为1 for(int x =i+1;x<len;x++ ) { if(nums[x]>nums[i]) { ret = max(ret,dfs(x,nums)+1);//求出以每一个下标为起点的子序列长度,并每次都更新一下 } } return ret;//返回最大值 } };但是以上代码是通不过的,因为时间限制:
那该怎么办呢?其实很简单,还是和前两道题一样要采用一个记忆化搜索的策略:
class Solution { public: int len; vector<int>memo; int lengthOfLIS(vector<int>& nums) { len = nums.size(); memo = vector<int>(len,1); int ret = 0; for(int i = 0;i<len;i++) { ret = max(ret,dfs(i,nums)); } return ret; } int dfs(int i,vector<int>&nums) { if(memo[i]!=1)//判断一下 { return memo[i]; } int ret = 1; for(int x =i+1;x<len;x++ ) { if(nums[x]>nums[i]) { ret = max(ret,dfs(x,nums)+1); } } memo[i] = ret;//记录一下 return ret; } };然后便过掉了:
4.猜数字游戏II
1.题目
我们正在玩一个猜数游戏,游戏规则如下:
- 我从
1到n之间选择一个数字。- 你来猜我选了哪个数字。
- 如果你猜到正确的数字,就会 赢得游戏 。
- 如果你猜错了,那么我会告诉你,我选的数字比你的 更大或者更小 ,并且你需要继续猜数。
- 每当你猜了数字
x并且猜错了的时候,你需要支付金额为x的现金。如果你花光了钱,就会 输掉游戏 。给你一个特定的数字
n,返回能够 确保你获胜 的最小现金数,不管我选择那个数字 。
2.题目接口
class Solution {
public:
int getMoneyAmount(int n) {
}
};3.解题思路
这道题该咋做呢?或者说这道题是什么意思呢?以输入一个数字10为例吧。我们要猜数字时便要在[1,10]之间猜测。于是我们猜数字策略便有很多种。比如一下几种:
1.当开始位置为1时
这里的至少要1+2+3+4+5+6+7+8块钱。
2.当我们一开始便选到5时:
还有一种便是这道题目给的最优解法:
在这个最优解法里边我们要做的便是找到这里的最大钱数也就是7+9 = 16。所以我们要做的便暴力搜索找出这个最优策略里的最大钱数。怎么做呢?其实还是遍历,抽象成下图:
这里一个一个试验的i便是为了得到最优模型而设计的。返回最大值便是为了得到每一个模型里面的最坏情况然后让每一个情况比较一下得到最优模型的最坏情况。写成代码如下:
class Solution { public: int getMoneyAmount(int n) { return dfs(1,n); } int dfs(int left,int right) { if(left>=right)//当数组范围中只有一个数字或者范围不合法时便返回0。 { return 0; } int ret = INT_MAX;//记录最优模型的最坏情况。 for(int head = left;head<right;head++) { int l = dfs(left,head-1)+head;//左结果 int r = dfs(head+1,right)+head;//右结果 ret = min(ret,max(l,r));//最优模型下的追怀情况 } return ret; } };这样便得到了代码了,这个代码是对的但是遗憾的是这个代码过不了:
接下来采用记忆化搜索方式:
class Solution { public: vector<vector<int>>memo; int getMoneyAmount(int n) { memo = vector<vector<int>>(n+1,vector<int>(n+1)); return dfs(1,n); } int dfs(int left,int right) { if(memo[left][right]!=0) { return memo[left][right]; } if(left>=right) { return 0; } int ret = INT_MAX; for(int head = left;head<right;head++) { int l = dfs(left,head-1)+head; int r = dfs(head+1,right)+head; ret = min(ret,max(l,r)); } memo[left][right] = ret; return ret; } };这样便可以过掉了:
总结:
其实记忆化搜索的目的便是实现剪枝操作,提高递归效率。当我们的递归操作里有大量的重复的递归操作时便可以用记忆化搜索的方式来提高递归效率。