目录
35.搜索插入位置
题意:
给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。
请必须使用时间复杂度为
O(log n)的算法。
【输入样例】nums = [1,3,5,6], target = 5
【输出样例】2
解题思路:最简单的二分查找,给定的是排序数组,直接根据数组下标,找到范围内的中点,并与target比较,如果比target大,则缩小查找范围为左区间;如果比target笑,缩小查找范围为右区间;如果相等,直接返回。
class Solution {
public int searchInsert(int[] nums, int target) {
int l =0;
int r = nums.length-1;
while(l<=r){
int mid = (l+r)/2;
if(nums[mid] == target){
return mid;
}else if(nums[mid]<target){
l=mid+1;
}else if(nums[mid]>target){
r=mid-1;
}
}
return l;
}
}时间: 击败了100.00%
内存: 击败了82.77%
74.搜索二维矩阵
题意:
给你一个满足下述两条属性的
m x n整数矩阵:
- 每行中的整数从左到右按非递减顺序排列。
- 每行的第一个整数大于前一行的最后一个整数。
给你一个整数
target,如果target在矩阵中,返回true;否则,返回false。
【输入样例】matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3
【输出样例】true
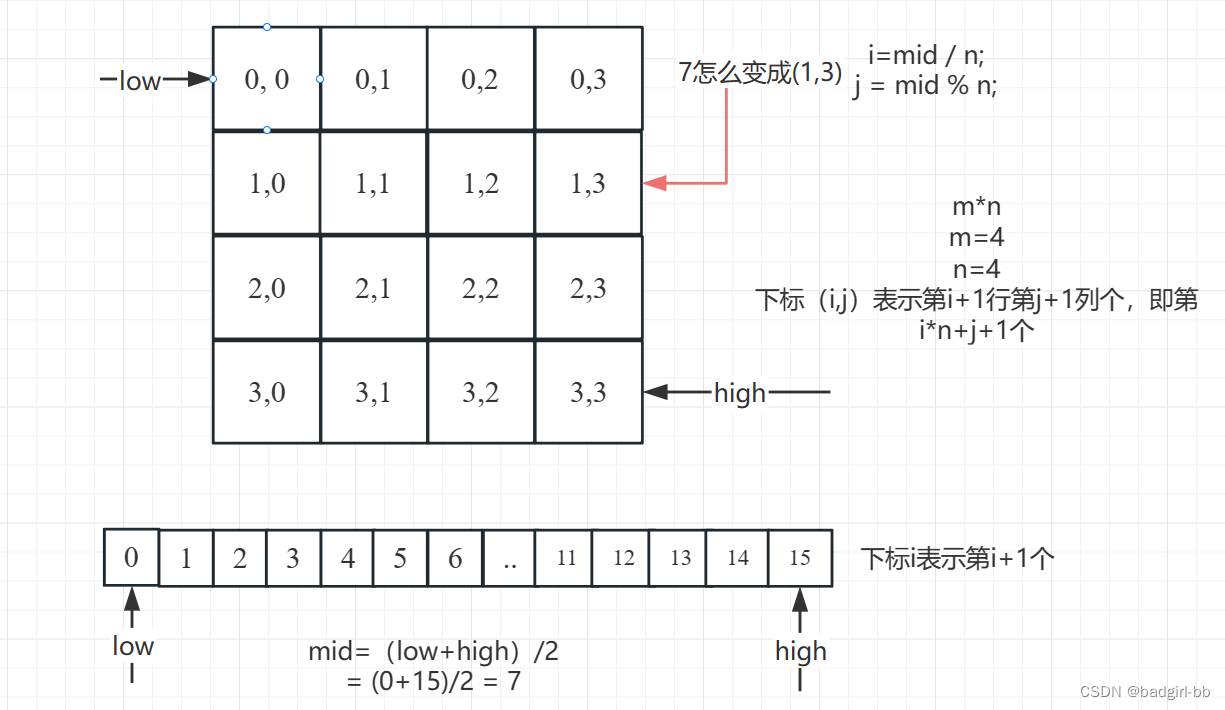
解题思路:原理与上一题一样,不过这里变成了二维矩阵。按照题目的要求,可以把二维矩阵看成一维数组,直接用上一题的方法,要注意的是下标之间的转换;
矩阵有m行n列,则在一维矩阵中,中间索引为mid,对应二维矩阵中的坐标为:
i = mid / n;//一行多少个数,能有多少整行
j = mid % n; //剩下当前行中有多少列
class Solution {
public boolean searchMatrix(int[][] matrix, int target) {
int m = matrix.length;
int n = matrix[0].length;
int low = 0, high = m * n - 1;
while(low <= high){
//这里有个坑,就是二维数组跟一维数组还不太一样,这里直接除之后还需要加上low
//加上low的特殊原因是保证mid可以代表其在一维数组中的真实坐标
int mid = (high - low) / 2 + low;
int x = matrix[mid/n][mid % n];
if(x < target){
low = mid + 1;
}else if(x > target){
high = mid - 1;
}else{
return true;
}
}
return false;
}
}时间: 击败了100.00%
内存: 击败了95.25%
162.寻找峰值
题意:
峰值元素是指其值严格大于左右相邻值的元素。
给你一个整数数组
nums,找到峰值元素并返回其索引。数组可能包含多个峰值,在这种情况下,返回 任何一个峰值 所在位置即可。你可以假设
nums[-1] = nums[n] = -∞。你必须实现时间复杂度为
O(log n)的算法来解决此问题。
【输入样例】nums =
[1,2,3,1]【输出样例】2
解题思路:寻找最大值。
class Solution {
public int findPeakElement(int[] nums) {
int n = nums.length;
int max = 0;
for(int i=1;i<nums.length;++i){
if(nums[i] > nums[max]){
max = i;
}
}
return max;
}
}时间: 击败了100.00%
内存: 击败了95.66%
33.搜索旋转排序数组
题意:
整数数组
nums按升序排列,数组中的值 互不相同 。在传递给函数之前,
nums在预先未知的某个下标k(0 <= k < nums.length)上进行了 旋转,使数组变为[nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]](下标 从 0 开始 计数)。例如,[0,1,2,4,5,6,7]在下标3处经旋转后可能变为[4,5,6,7,0,1,2]。给你 旋转后 的数组
nums和一个整数target,如果nums中存在这个目标值target,则返回它的下标,否则返回-1。你必须设计一个时间复杂度为
O(log n)的算法解决此问题。
【输入样例】nums = [
4,5,6,7,0,1,2], target = 0【输出样例】4
解题思路:先二分查找找到mid,如果left<mid,证明[left,mid]范围是有序的,还是用传统的二分查找找;否则[left,mid]无序,重新进行分割。
对于[mid,right]也是如此,如果mid<right,继续查找;否则还是继续分割。
class Solution {
public int search(int[] nums, int target) {
int low = 0,high = nums.length - 1;
while(low <= high){
int mid = (low + high) /2;
if(nums[mid] == target) return mid;
if(nums[low] <= nums[mid]){
if (target >= nums[low] && target < nums[mid]){
high = mid - 1;
}else{
low = mid + 1;
}
}else{
if (target > nums[mid] && target <= nums[high]){
low = mid + 1;
} else{
high = mid - 1;
}
}
}
return -1;
}
}时间: 击败了100.00%
内存: 击败了80.30%