【强化学习原理+项目专栏】必看系列：单智能体、多智能体算法原理+项目实战、相关技巧（调参、画图等、趣味项目实现、学术应用项目实现

专栏详细介绍：【强化学习原理+项目专栏】必看系列：单智能体、多智能体算法原理+项目实战、相关技巧（调参、画图等、趣味项目实现、学术应用项目实现

对于深度强化学习这块规划为：

• 基础单智能算法教学（gym环境为主）
• 主流多智能算法教学（gym环境为主）
  • 主流算法：DDPG、DQN、TD3、SAC、PPO、RainbowDQN、QLearning、A2C等算法项目实战
• 一些趣味项目（超级玛丽、下五子棋、斗地主、各种游戏上应用）
• 单智能多智能题实战（论文复现偏业务如：无人机优化调度、电力资源调度等项目应用）

本专栏主要方便入门同学快速掌握强化学习单智能体|多智能体算法原理+项目实战。后续会持续把深度学习涉及知识原理分析给大家，让大家在项目实操的同时也能知识储备，知其然、知其所以然、知何由以知其所以然。

声明：部分项目为网络经典项目方便大家快速学习，后续会不断增添实战环节（比赛、论文、现实应用等）

• 专栏订阅（个性化选择）：

  • 强化学习原理+项目专栏大合集-《推荐订阅☆☆☆☆☆》

  • 强化学习单智能体算法原理+项目实战《推荐订阅☆☆☆☆》

  • 强化学习多智能体原理+项目实战《推荐订阅☆☆☆☆☆》

  • 强化学习相关技巧（调参、画图等《推荐订阅☆☆☆》）

  • tensorflow_gym-强化学习:免费《推荐订阅☆☆☆☆》

  • 强化学习从基础到进阶-案例与实践：免费《推荐订阅☆☆☆☆☆》

强化学习从基础到进阶-案例与实践[6]：演员-评论员算法（advantage actor-critic，A2C），异步A2C、与生成对抗网络的联系等详解

强化学习全系列超详细算法码源见文章顶部

在REINFORCE算法中，每次需要根据一个策略采集一条完整的轨迹，并计算这条轨迹上的回报。这种采样方式的方差比较大，学习效率也比较低。我们可以借鉴时序差分学习的思想，使用动态规划方法来提高采样效率，即从状态 $s$ 开始的总回报可以通过当前动作的即时奖励 $r(s,a,s^{\prime })$ 和下一个状态 $s^{\prime }$ 的值函数来近似估计。

演员-评论员算法是一种结合策略梯度和时序差分学习的强化学习方法，其中，演员是指策略函数 ${\pi }_{\theta }(a|s)$，即学习一个策略以得到尽可能高的回报。评论员是指价值函数 $V_{\pi }(s)$，对当前策略的值函数进行估计，即评估演员的好坏。借助于价值函数，演员-评论员算法可以进行单步参数更新，不需要等到回合结束才进行更新。在演员-评论员算法里面，最知名的算法就是异步优势演员-评论员算法。如果我们去掉异步，则为优势演员-评论员（advantage actor-critic，A2C）算法。A2C算法又被译作优势演员-评论员算法。如果我们加了异步，变成异步优势演员-评论员算法。

1.策略梯度回顾

我们复习一下策略梯度，在更新策略参数 $\theta$ 的时候，我们可以通过
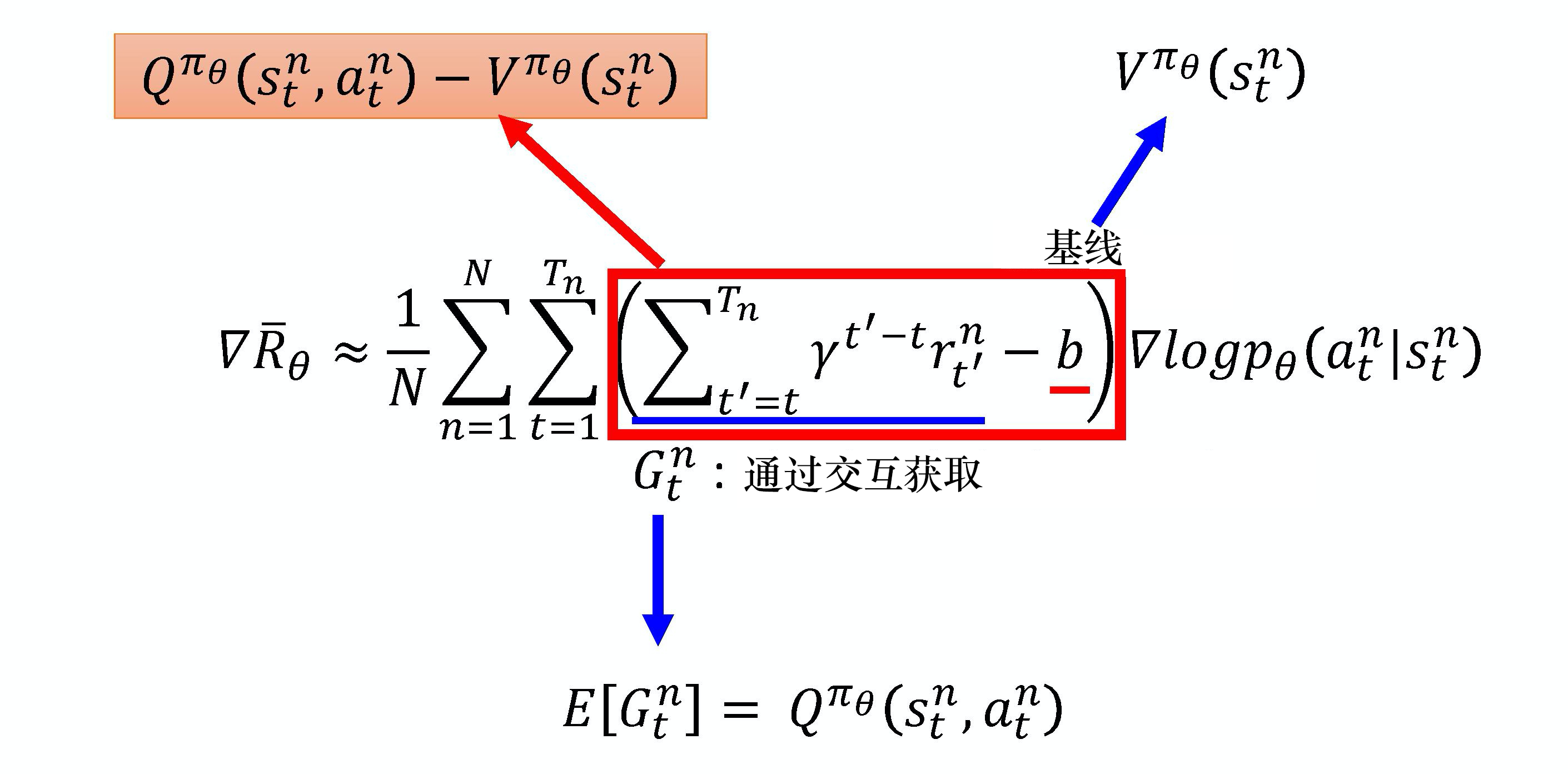
$$\nabla {\bar{R}}_{\theta }\approx \frac{1}{N}\sum _{n=1}^N\sum _{t=1}^{T_n}\left(\sum _{t^{\prime }=t}^{T_n}{\gamma }^{t^{\prime }-t}{r}_{t^{\prime }}^n-b\right)\nabla \log p_{\theta }\left(a_t^n\mid s_t^n\right)\text{\hspace{1em}(6.1)}$$
来计算梯度。式(6.1)表示我们首先通过智能体与环境的交互，可以计算出在某一个状态 $s$ 采取某一个动作 $a$ 的概率 $p_{\theta }(a_t|s_t)$。接下来，我们计算在某一个状态 $s$ 采取某一个动作 $a$ 之后直到游戏结束的累积奖励。${\sum }_{t^{\prime }=t}^{T_n}{\gamma }^{t^{\prime }-t}{r}_{t^{\prime }}^n$ 表示我们把从时间 $t$ 到时间 $T$ 的奖励相加，并且在前面乘一个折扣因子，通常将折扣因子设置为 0.9 或 0.99等数值，与此同时也会减去一个基线值 $b$，减去值 $b$ 的目的是希望括号里面这一项是有正有负的。如果括号里面这一项是正的，我们就要增大在这个状态采取这个动作的概率；如果括号里面是负的，我们就要减小在这个状态采取这个动作的概率。

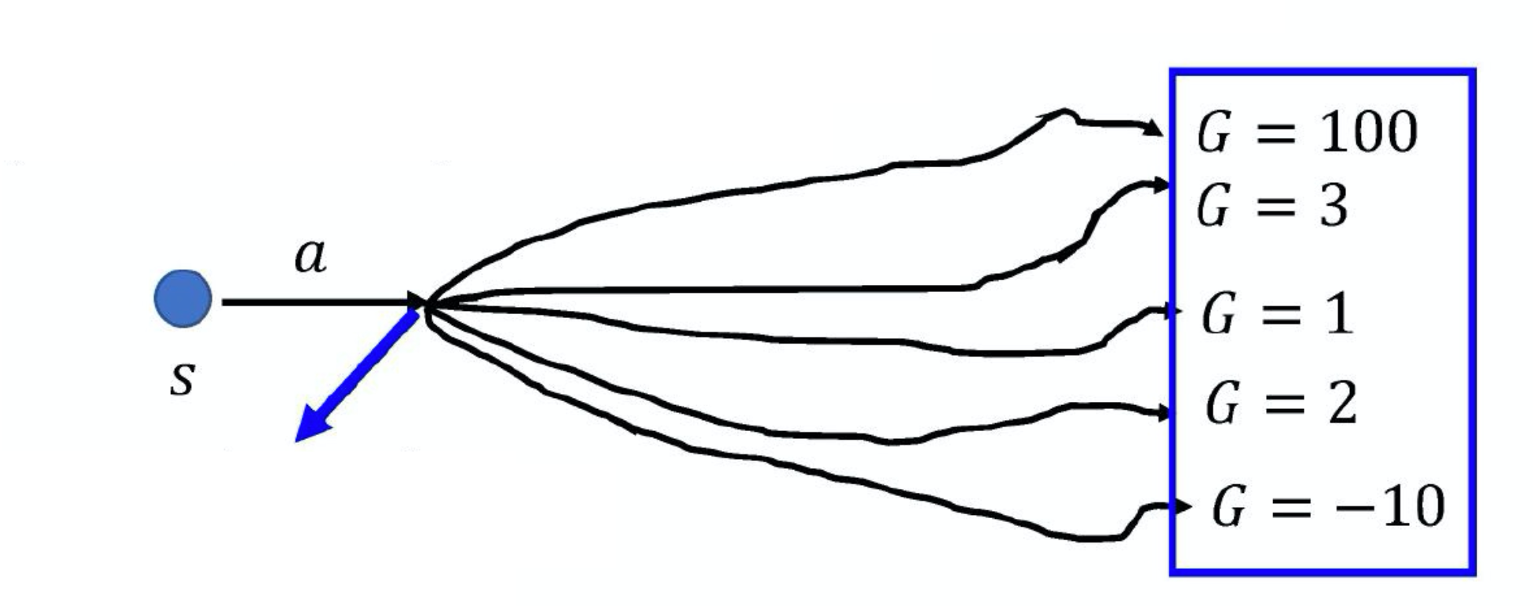
我们使用 $G$ 表示累积奖励，$G$ 是非常不稳定的。因为交互的过程本身具有随机性，所以在某一个状态 $s$ 采取某一个动作 $a$ 时计算得到的累积奖励，每次结果都是不同的，因此 $G$ 是一个随机变量。对于同样的状态 $s$ 和同样的动作 $a$，$G$ 可能有一个固定的分布。但由于我们采取采样的方式，因此我们在某一个状态 $s$ 采取某一个动作 $a$ 一直到游戏结束，统计一共得到了多少的奖励，我们就把它当作 $G$。

如图 6.1 所示，如果我们把 $G$ 想成一个随机变量，实际上是在对 $G$ 做采样，用这些采样的结果去更新参数。但实际上在某一个状态 $s$ 采取某一个动作 $a$，接下来会发生什么事，其本身是有随机性的。虽然说有一个固定的分布，但其方差可能会非常大。智能体在同一个状态采取同一个动作时，最后得到的结果可能会是很不一样的。当然，假设我们在每次更新参数之前，都可以采样足够多次，那当然就没有以上的问题了。但我们每次做策略梯度，每次更新参数之前都要做一些采样时，采样的次数是不可能太多的，我们只能够做非常少量的采样。如果我们正好采样到差的结果，比如采样到 $G=100$、采样到 $G=-10$，显然结果会是很差的。

2.深度Q网络回顾

Q：我们能不能让整个训练过程变得稳定，能不能直接估测随机变量 $G$ 的期望值？

A：我们直接用一个网络去估测在状态 $s$ 采取动作 $a$ 时 $G$ 的期望值。如果这样是可行的，那么在随后的训练中我们就用期望值代替采样的值，这样就会让训练变得更加稳定。

Q：怎么使用期望值代替采样的值呢？

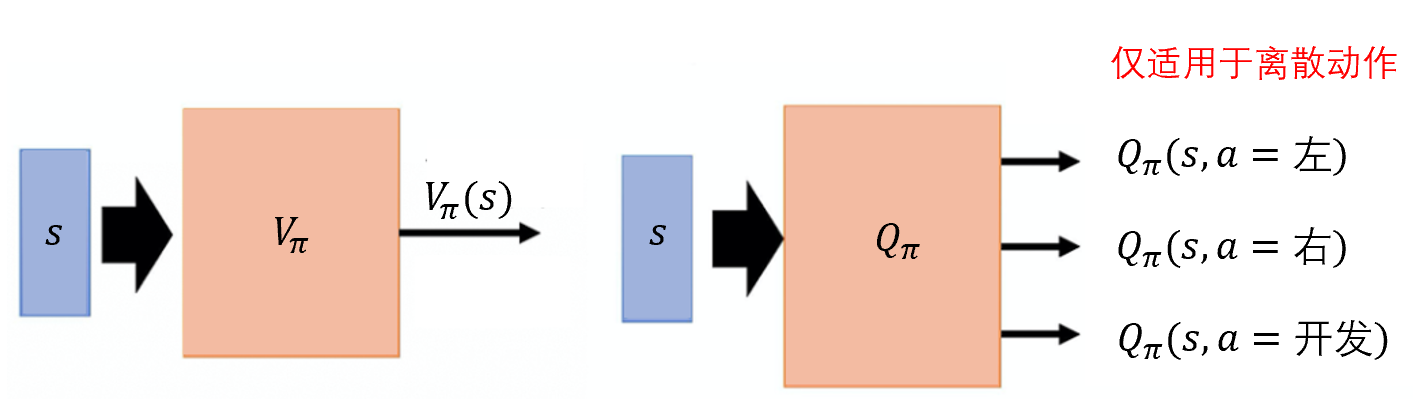
A：这里就需要引入基于价值的（value-based）的方法。基于价值的方法就是 深度Q网络 。深度Q网络 有两种函数，有两种评论员。如图 6.2 所示，第一种评论员是 $V_{\pi }(s)$。即假设演员的策略是 $\pi$，使用 $\pi$ 与环境交互，当智能体看到状态 $s$ 时，接下来累积奖励的期望值是多少。第二种评论员是 $Q_{\pi }(s,a)$。$Q_{\pi }(s,a)$ 把 $s$ 与 $a$ 当作输入，它表示在状态 $s$ 采取动作 $a$，接下来用策略 $\pi$ 与环境交互，累积奖励的期望值是多少。$V_{\pi }$ 接收输入 $s$，输出一个标量。$Q_{\pi }$ 接收输入 $s$，它会给每一个 $a$ 都分配一个 Q值。

3.优势演员-评论员算法

如图 6.3 所示，随机变量 $G$ 的期望值正好就是 Q 值，即
$$\mathbb{E}\left[G_t^n\right]=Q_{{\pi }_{\theta }}\left(s_t^n,a_t^n\right)$$
此也为 Q 函数的定义。Q函数的定义就是在某一个状态 $s$，采取某一个动作 $a$，假设策略是 $\pi$ 的情况下所能得到的累积奖励的期望值，即 $G$ 的期望值。累积奖励的期望值就是 $G$ 的期望值。所以假设用 $\mathbb{E}\left[G_t^n\right]$ 来代表 ${\sum }_{t^{\prime }=t}^{T_n}{\gamma }^{t^{\prime }-t}{r}_{t^{\prime }}^n$ 这一项，把Q函数套在这里就结束了，我们就可以把演员与评论员这两个方法结合起来。

有不同的方法表示基线，一个常见的方法是用价值函数 $V_{{\pi }_{\theta }}\left(s_t^n\right)$ 来表示基线。价值函数的定义为，假设策略是 $\pi$，其在某个状态 $s$ 一直与环境交互直到游戏结束，期望奖励有多大。 $V_{{\pi }_{\theta }}\left(s_t^n\right)$ 没有涉及动作，$Q_{{\pi }_{\theta }}\left(s_t^n,a_t^n\right)$ 涉及动作。
$V_{{\pi }_{\theta }}\left(s_t^n\right)$ 是 $Q_{{\pi }_{\theta }}\left(s_t^n,a_t^n\right)$ 的期望值， $Q_{{\pi }_{\theta }}\left(s_t^n,a_t^n\right)-V_{{\pi }_{\theta }}\left(s_t^n\right)$ 会有正有负，所以 ${\sum }_{t^{\prime }=t}^{T_n}{\gamma }^{t^{\prime }-t}{r}_{t^{\prime }}^n-b$ 这一项就会有正有负。所以我们就把策略梯度里面 ${\sum }_{t^{\prime }=t}^{T_n}{\gamma }^{t^{\prime }-t}{r}_{t^{\prime }}^n-b$ 这一项换成了优势函数$A^{\theta }\left(s_t^n,a_t^n\right)$，即 $Q_{{\pi }_{\theta }}\left(s_t^n,a_t^n\right)-V_{{\pi }_{\theta }}\left(s_t^n\right)$。因此该算法称为优势演员-评论员算法。

如果我们这么实现，有一个缺点，即我们需要估计两个网络————Q网络和 V网络，估计不准的风险就变成原来的两倍。所以我们何不只估计一个网络呢？事实上，在演员-评论员算法中，我们可以只估计网络 V，并利用 $V$ 的值来表示 $Q$ 的值，$Q_{\pi }\left(s_t^n,a_t^n\right)$ 可以写成 $ r_{t}^{{n}+V_{\pi}\left(s_{t+1}}{n}\right)$ 的期望值，即
$$Q_{\pi }\left(s_t^n,a_t^n\right)=\mathbb{E}\left[r_t^n+V_{\pi }\left(s_{t+1}^n\right)\right]$$

在状态 $s$ 采取动作 $a$，我们会得到奖励 $r$，进入状态 $s_{t+1}$。但是我们会得到什么样的奖励 $r$，进入什么样的状态 $s_{t+1}$，这件事本身是有随机性的。所以要把$r_t^n+V_{\pi }\left(s_{t+1}^n\right)$取期望值才会等于Q函数的值。但我们现在把取期望值去掉，即
$$Q_{\pi }\left(s_t^n,a_t^n\right)=r_t^n+V_{\pi }\left(s_{t+1}^n\right)$$

我们就可以把Q函数的值用 $r_t^n+V_{\pi }\left(s_{t+1}^n\right)$ 取代，可得
$$r_t^n+V_{\pi }\left(s_{t+1}^n\right)-V_{\pi }\left(s_t^n\right)$$

把取期望值去掉的好处就是我们不需要估计 $Q$ 了，只需要估计 $V$。但与此同时我们会引入一个随机的参数 $r$。$r$ 是有随机性的，它是一个随机变量，但是 $r$ 相较于累积奖励 $G$ 是一个较小的值，因为它是某一个步骤得到的奖励，而 $G$ 是所有未来会得到的奖励的总和，$G$ 的方差比较大。$r$ 虽然也有一些方差，但它的方差比 $G$ 的要小。所以把原来方差比较大的 $G$ 换成方差比较小的 $r$ 也是合理的。

Q：为什么我们可以直接把取期望值去掉？

A：原始的异步优势演员-评论员算法的论文尝试了各种方法，最后发现这个方法最好。当然有人可能会有疑问，说不定估计 $Q$ 和 $V$ 也可以估计得很好，但实际做实验的时候，最后结果就是这个方法最好，所以后来大家都使用了这个方法。

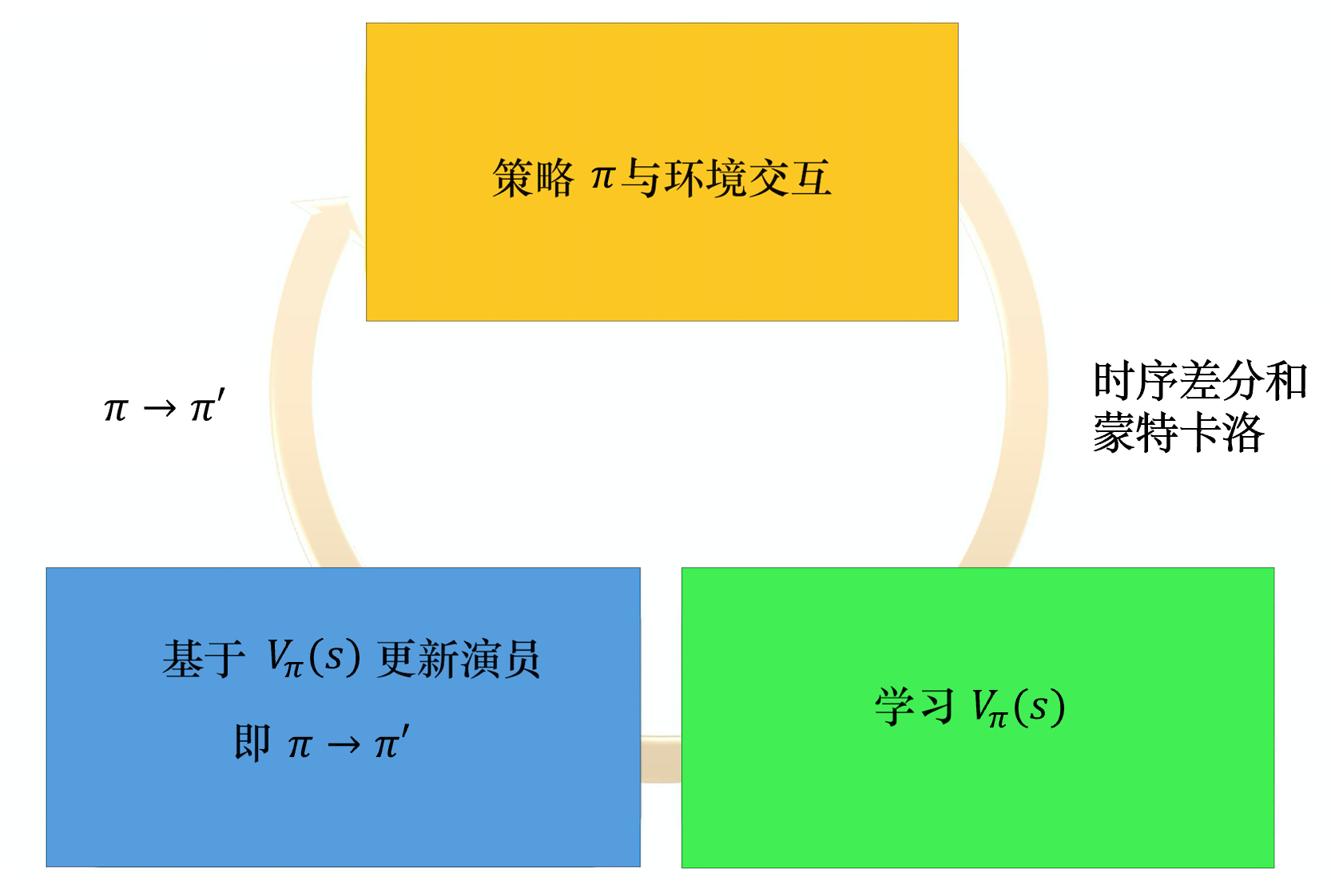
优势演员-评论员算法的流程如图 6.5 所示，我们有一个 $\pi$，有个初始的演员与环境交互，先收集资料。在策略梯度方法里收集资料以后，就来更新策略。但是在演员-评论员算法里面，我们不是直接使用那些资料来更新策略。我们先用这些资料去估计价值函数，可以用 时序差分方法 或 蒙特卡洛方法 来估计价值函数。接下来，我们再基于价值函数，使用式(6.2)更新 $\pi$。
$$\nabla {\bar{R}}_{\theta }\approx \frac{1}{N}\sum _{n=1}^N\sum _{t=1}^{T_n}\left(r_t^n+V_{\pi }\left(s_{t+1}^n\right)-V_{\pi }\left(s_t^n\right)\right)\nabla \log p_{\theta }\left(a_t^n\mid s_t^n\right)\text{\hspace{1em}(6.2)}$$
有了新的 $\pi$ 以后，再与环境交互，收集新的资料，去估计价值函数。再用新的价值函数更新策略，更新演员。整个优势演员-评论员算法就是这么运作的。

实现优势演员-评论员算法的时候，有两个一定会用到的技巧。第一个技巧是，我们需要估计两个网络：$V$ 网络和策略的网络（也就是演员）。评论员网络 $V_{\pi }(s)$ 接收一个状态，输出一个标量。演员的策略 $\pi (s)$ 接收一个状态，如果动作是离散的，输出就是一个动作的分布。如果动作是连续的，输出就是一个连续的向量。

图 6.5 所示为离散动作的例子，连续动作的情况也是一样的。输入一个状态，网络决定现在要采取哪一个动作。演员网络和评论员网络的输入都是 $s$，所以它们前面几个层（layer）是可以共享的。

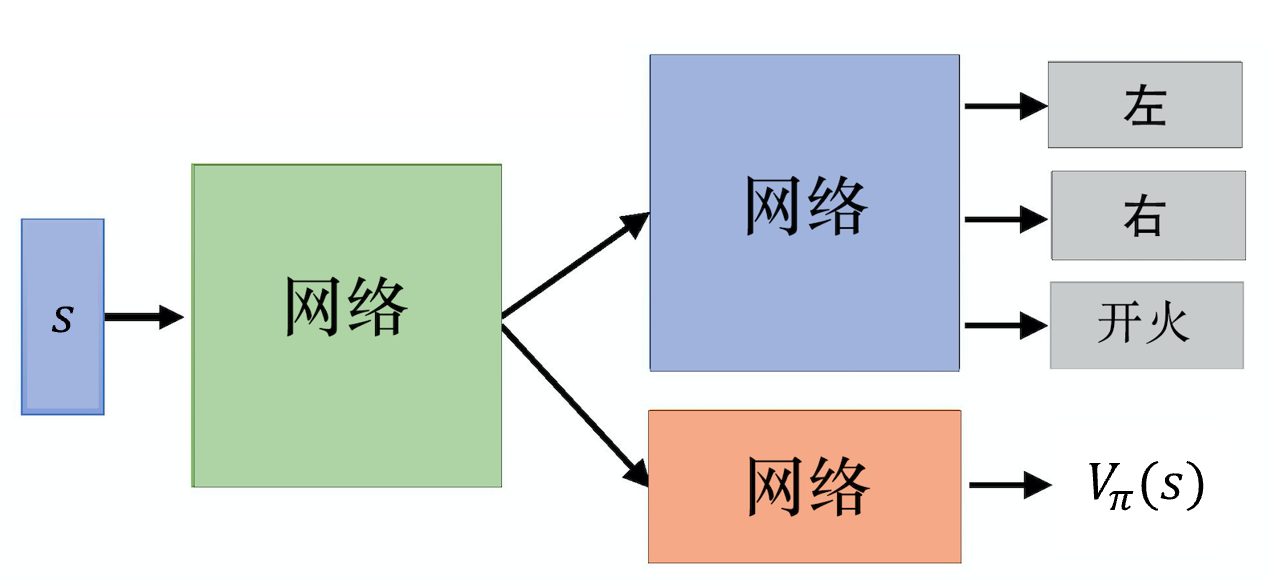
尤其当我们在玩雅达利游戏时，输入都是图像。输入的图像非常复杂，通常我们在前期都会用一些卷积神经网络来处理它们，把图像抽象成高级（high level）的信息。把像素级别的信息抽象成高级信息的特征提取器，对于演员与评论员来说是可以共用的。所以通常我们会让演员与评论员共享前面几层，并且共用同一组参数，这一组参数大部分都是卷积神经网络的参数。先把输入的像素变成比较高级的信息，再让演员决定要采取什么样的动作，让评论员即价值函数计算期望奖励。

第二个技巧是我们需要探索的机制。在演员-评论员算法中，有一个常见的探索的方法是对 $\pi$ 输出的分布设置一个约束。这个约束用于使分布的熵（entropy）不要太小，也就是希望不同的动作被采用的概率平均一些。这样在测试的时候，智能体才会多尝试各种不同的动作，才会把环境探索得比较好，从而得到比较好的结果。

4.异步优势演员-评论员算法

强化学习有一个问题，就是它很慢，怎么提高训练的速度呢？例如，如图 6.6 所示，在动漫《火影忍者》中，有一次鸣人想要在一周之内打败晓，所以要加快修行的速度，鸣人的老师就教他一个方法：用影分身进行同样的修行。两个一起修行，经验值累积的速度就会变成两倍，所以鸣人就使用了 1000 个影分身来进行修行。这就是异步优势演员-评论员算法的体现。

异步优势演员-评论员算法同时使用很多个进程（worker），每一个进程就像一个影分身，最后这些影分身会把所有的经验值集合在一起。如果我们没有很多 CPU，不好实现异步优势演员-评论员算法，但可以实现优势演员-评论员算法。

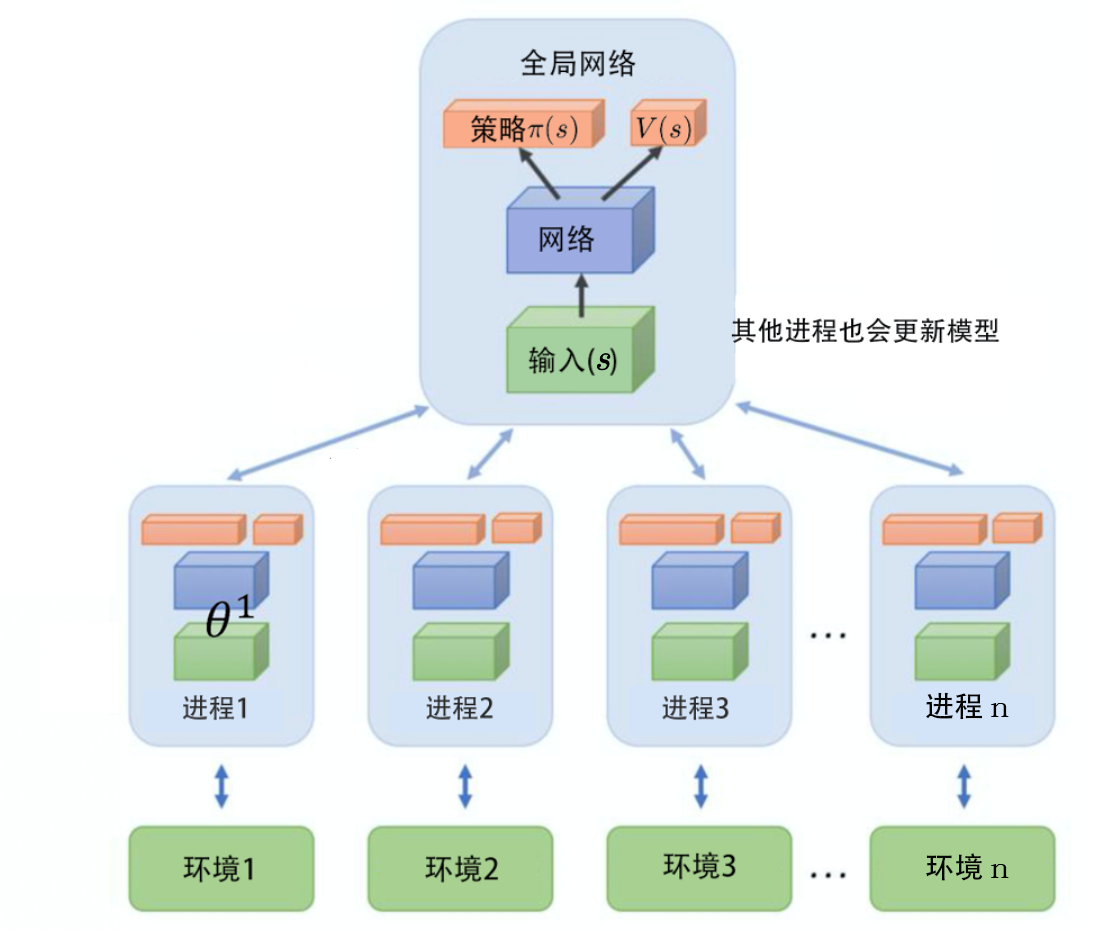
异步优势演员-评论员算法的运作流程，如图 6.7 所示，异步优势演员-评论员算法一开始有一个全局网络（global network）。全局网络包含策略网络和价值网络，这两个网络是绑定（tie）在一起的，它们的前几个层会被绑在一起。
假设全局网络的参数是 ${\theta }_1$，我们使用多个进程，每个进程用一张 CPU 去跑。比如我们有 8 个进程，则至少 8 张 CPU。每一个进程在工作前都会把全局网络的参数复制过来。接下来演员就与环境交互，每一个演员与环境交互的时候，都要收集到比较多样的数据。例如，如果是走迷宫，可能每一个演员起始的位置都会不一样，这样它们才能够收集到比较多样的数据。每一个演员与环境交互完之后，我们就会计算出梯度。计算出梯度以后，要用梯度去更新参数。我们就计算一下梯度，用梯度去更新全局网络的参数。就是这个进程算出梯度以后，就把梯度传回给中央的控制中心，中央的控制中心就会用这个梯度去更新原来的参数。

注意，A3C使用了平行探索的方法，所有的演员都是平行跑的，每一个演员各做各的，不管彼此。所以每个演员都是去要了一个参数以后，做完就把参数传回去。当第一个进程做完想要把参数传回去的时候，本来它要的参数是 ${\theta }_1$，等它要把梯度传回去的时候，可能别人已经把原来的参数覆盖掉，变成 ${\theta }_2$了。但是没有关系，它一样会把这个梯度就覆盖过去。

5.路径衍生策略梯度

接下来我们来了解**路径衍生策略梯度（pathwise derivative policy gradient）**方法。这个方法可以看成 深度Q网络 解连续动作的一种特别的方法，也可以看成一种特别的演员-评论员的方法。用动漫《棋魂》来比喻，阿光就是一个演员，佐为就是一个评论员。阿光落某一子以后，如果佐为是一般的演员-评论员算法的评论员，他会告诉阿光这时候不应该下小马步飞。佐为会告诉我们，我们现在采取的这一步算出来的值到底是好还是不好，但这样就结束了，他只告诉我们好还是不好。因为一般的演员-评论员算法的评论员就是输入状态或输入状态-动作对，给演员一个值，所以对演员来说，它只知道它做的这个动作到底是好还是不好。

但在路径衍生策略梯度里面，评论员会直接告诉演员采取什么样的动作才是好的。所以佐为不只是告诉阿光，这个时候不要下小马步飞，同时还告诉阿光这个时候应该要下大马步飞，这就是路径衍生策略梯度中的评论员所做的。评论员会直接告诉演员做什么样的动作才可以得到比较大的值。

从 深度Q网络 的观点来看，深度Q网络 的一个问题是在使用 深度Q网络 时，考虑连续向量会比较麻烦，没有通用的解决方法（general solution），那我们应该怎么解这个优化问题呢？我们用一个演员来解决这个优化的问题。本来在深度Q网络 里面，如果是一个连续的动作，我们要解决这个优化问题。但是现在这个优化问题由演员来解决，假设演员就是一个解决者（solver），这个解决者的工作就是对于给定的状态 $s$，解出来哪一个动作可以得到最大的 Q 值，这是从另外一个观点来看路径衍生策略梯度。在生成对抗网络 中也有类似的说法。我们学习一个判别器（discriminator）并用于评估时，是非常困难的，因为我们要解决的 arg max 的问题非常的困难，所以用生成器（generator）来生成。所以概念是一样的，Q 就是那个判别器。根据这个判别器决定动作非常困难，怎么办？另外学习一个网络来解决这个优化问题，这个网络就是演员。所以两个不同的观点是同一件事。从两个不同的观点来看，一个观点是：我们可以对原来的深度Q网络 加以改进，学习一个演员来决定动作以解决 arg max 不好解的问题。另外一个观点是：原来的演员-评论员算法的问题是评论员并没有给演员足够的信息，评论员只告诉演员好或不好的，没有告诉演员什么样是好，现在有新的方法可以直接告诉演员什么样的是好的。路径衍生策略梯度算法如图 6.8 所示，假设我们学习了一个Q函数，Q函数的输入是 $s$ 与 $a$，输出是 $Q_{\pi }(s,a)$。接下来，我们要学习一个演员，这个演员的工作就是解决 arg max 的问题，即输入一个状态 $s$，希望可以输出一个动作 $a$。$a$ 被代入Q函数以后，它可以让 $Q_{\pi }(s,a)$ 尽可能大，即
$${\pi }^{\prime }(s)=\underset{a}{\mathrm{argmax}}{Q}_{\pi }(s,a)$$

实际上在训练的时候，我们就是把 Q 与演员连接起来变成一个比较大的网络。Q 是一个网络，接收输入 $s$ 与 $a$，输出一个值。演员在训练的时候，它要做的事就是接收输入 $s$，输出 $a$。把 $a$ 代入 Q 中，希望输出的值越大越好。我们会固定住 Q 的参数，只调整演员的参数，用梯度上升的方法最大化 Q 的输出，这就是一个 生成对抗网络，即有条件的生成对抗网络（conditional GAN）。Q 就是判别器，但在强化学习里就是评论员，演员在 生成对抗网络 里面就是生成器。

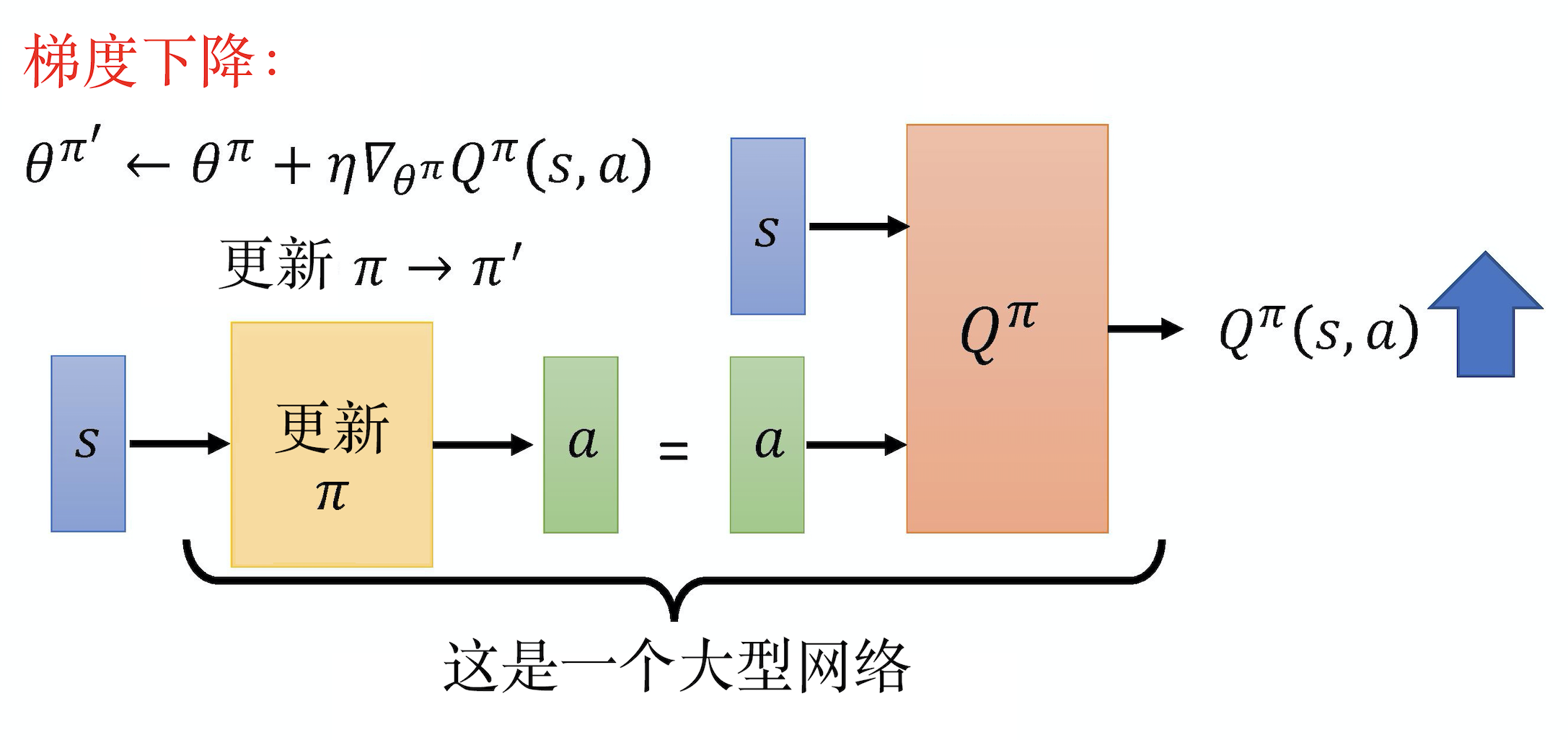
我们来看一下路径衍生策略梯度算法。如图 6.9 所示，一开始会有一个策略 $\pi$，它与环境交互并估计 Q 值。估计完 Q 值以后，我们就把 Q 值固定，只去学习一个演员。假设这个 Q 值估得很准，它知道在某一个状态采取什么样的动作会得到很大的Q值。接下来就学习这个演员，演员在给定 $s$ 的时候，采取了 $a$，可以让最后Q函数算出来的值越大越好。我们用准则（criteria）去更新策略 $\pi$，用新的 $\pi$ 与环境交互，再估计 Q值，得到新的 $\pi$ 去最大化 Q值的输出。深度Q网络 里面的技巧，在这里也几乎都用得上，比如经验回放、探索等技巧。

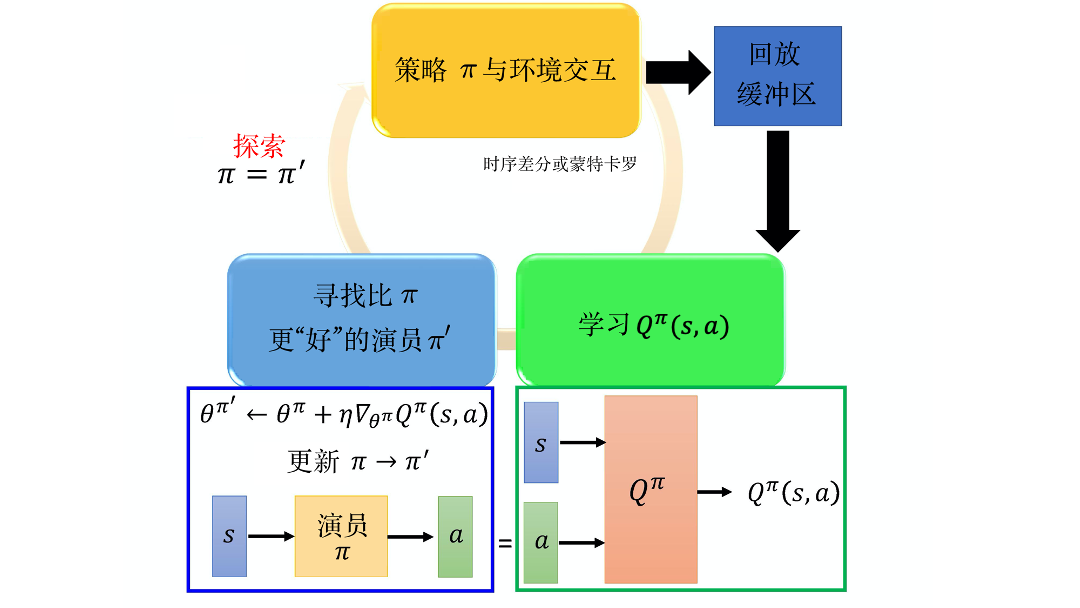
图 6.10 所示为原来深度Q网络的算法。我们有一个Q函数 $Q$ 和另外一个目标Q函数 $\hat{Q}$。每一次训练，在每一个回合的每一个时间点，我们会看到一个状态 $s_t$，会采取某一个动作 $a_t$。至于采取哪一个动作是由Q函数所决定的。如果是离散动作，我们看哪一个动作 $a$ 可以让 Q 值最大，就采取哪一个动作。当然，我们需要加一些探索，这样表现才会好。我们会得到奖励 $r_t$，进入新的状态 $s_{t+1}$，然后把 $(s_t$,$a_t$,$r_t$,$s_{t+1})$ 放到回放缓冲区里。接下来，我们会从回放缓冲区中采样一个批量的数据，在这个批量数据里面，可能某一笔数据是 $(s_i,a_i,r_i,s_{i+1})$。接下来我们会算一个目标 $y$ ，$y=r_i+{\max }_a\hat{Q}\left(s_{i+1},a\right)$。怎么学习 Q 呢？我们希望 $Q(s_i,a_i)$ 与 $y$ 越接近越好，这是一个回归问题，最后每 $C$ 步，要用 $Q$ 替代 $\hat{Q}$ 。

接下来我们把深度Q网络 改成路径衍生策略梯度，需要做4个改变，如图 6.11 所示。

（1）第一个改变是，我们要把 $Q$ 换成 $\theta$，本来是用 $Q$ 来决定在状态 $s_t$ 执行一个动作 $a_t$， 现在直接用 $\theta$ 来执行动作。
我们直接学习了一个演员。这个演员的输入 $s_t$ 会告诉我们应该采取哪一个 $a_t$。所以本来输入 $s_t$，采取哪一个 $a_t$是 Q 决定的，而在路径衍生策略梯度里面，我们会直接用 $\theta$ 来决定。

（2）第二个改变是，本来我们要计算在 $s_{i+1}$，根据策略采取某一个动作 $a$ 会得到的 Q 值，我们会采取让 $\hat{Q}$ 最大的那个动作 $a$。现在因为我们直接把 $s_{i+1}$ 代入$\theta$ ，就会知道给定 $s_{i+1}$ ，哪个动作会给我们最大的 Q值，就采取哪个动作。在Q函数里面，有两个Q网络：真正的 Q网络和目标 Q 网络。实际上我们在实现路径衍生策略梯度算法的时候，也有两个演员：真正要学习的演员$\theta$和目标演员$\hat{\theta }$。这个原理就与为什么要有目标 Q 网络一样，我们在算目标值的时候，并不希望它一直的变动，所以我们会有一个目标演员和一个目标Q函数，它们平常的参数就是固定住的，这样可以让目标的值不会一直地变化。

总结一下，第二个改变是我们用策略取代原来要解 arg max 的地方。

（3）第三个改变是，之前只要学习 Q函数，现在我们多学习了一个 $\theta$，学习 $\theta$ 的目的是最大化Q函数，希望得到的演员可以让Q函数的输出尽可能大，这与学习 生成对抗网络 里面的生成器的概念是类似的。

（4）第四个改变是，我们不仅要取代目标的 Q 网络，还要取代目标策略。

6.与生成对抗网络的联系

如表 6.1 所示，GAN 与演员-评论员的方法是非常类似的。如果大家感兴趣，可以参考一篇论文：“Connecting Generative Adversarial Network and Actor-Critic Methods”。

生成对抗网络与演员-评论员都挺难训练，所以在文献上就有各式各样的方法，告诉我们怎么样可以训练 生成对抗网络。知道生成对抗网络与演员-评论员非常相似后，我们就可以知道怎样训练演员-评论员。但是因为做 生成对抗网络 与演员-评论员的人是两群人，所以这篇论文里面就列出说在生成对抗网络上面有哪些技术是有人做过的，在演员-评论员上面，有哪些技术是有人做过的。也许训练 生成对抗网络 的技术，我们可以试着应用在演员-评论员上，在演员-评论员上用过的技术，也可以试着应用在生成对抗网络上。

• 参考文献
  • 神经网络与深度学习