需要在 Excel 中求一个数字的平方根吗?使用几个内置的 Excel 函数和公式可以轻松计算平方根。在本分步指南中,您将学习在 Excel 中计算平方根的 5 种不同方法,包括使用 SQRT 函数、POWER 函数、指数公式、VBA 代码和 Power Query。跟随教程,掌握平方根计算并提高您的 Excel 技能。让我们深入了解一下吧!
使用 SQRT 函数
在 Excel 中计算平方根的最简单方法是使用 SQRT 函数。SQRT 代表平方根,返回给定数字的平方根
要使用 SQRT:
- 在单元格中输入您想要计算平方根的数字,例如 A1。
- 在另一个单元格中,输入 =SQRT(A1)。
-
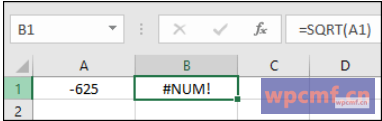
- 按 Enter 键,将显示平方根结果。
- 例如,如果 A1 包含 625,=SQRT(A1) 将返回 25,因为 25 是 625 的平方根。
-
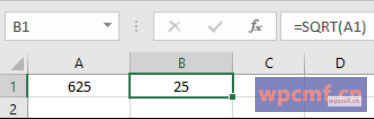
SQRT 函数适用于正数和负数。对于底片,将其与 ABS 功能结合起来:
=SQRT(ABS(A1))
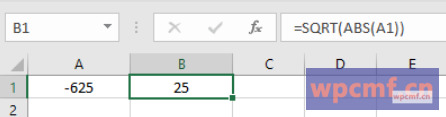
这会在计算平方根之前将数字转换为正数
使用POWER功能
在 Excel 中求平方根的另一种方法是使用 POWER 函数。
POWER 返回提供的指数幂的数字。
使用 POWER 求平方根:
- 在单元格中输入目标编号,例如 A1。
- 使用 =POWER(A1, 0.5),将 A1 提高到 1/2 次方。
- 按 Enter 键查看结果。
- 0.5 相当于 1/2,计算平方根。
-
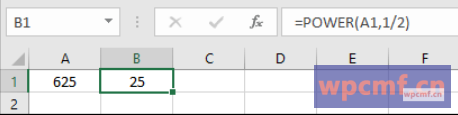
- 因此 =POWER(A1, 0.5) 产生与 =SQRT(A1) 相同的结果。POWER 为其他根(如立方体)提供了更大的灵活性
使用指数公式
您还可以使用 Excel 的指数运算符 ^ 而不是函数来计算平方根:
- 在单元格中输入目标编号,例如 A1。
- 在另一个单元格中,使用 =A1^(1/2)
- 按 Enter 键查看平方根结果。
- 这是有效的,因为 1/2 的计算结果为 0.5,在用作指数时执行平方根计算
这种公式方法允许添加逻辑,例如除平方之外的根:
- 平方根:A1^(1/2)
- 立方根:A1^(1/3)
- 四次方根:A1^(1/4)等
因此,如果您需要更高级的根,请使用指数公式。
使用 VBA 代码求平方根
要在没有公式的情况下计算平方根,可以使用 VBA 代码
例如:
子平方根()
告诉我是否为整数
数量 = 25
MsgBox “” & num & ” 的平方根是 ” & Sqr(num)
这将数字存储在变量中,然后使用 VBA 的内置 Sqr 函数显示其平方根
您可以增强代码以接受输入、验证数字、处理错误等。VBA 对于执行重复的 Excel 任务非常强大





