一、基础知识
1、一阶微分方程
 称为一阶微分方程。y(x0)=y0为定解条件。
称为一阶微分方程。y(x0)=y0为定解条件。
其常规求解方法:
(1)变量分离
再两边积分就可以求出通解。
(2)一阶线性求解公式
![]()
通解公式:
有些一阶微分方程需要通过整体代换,比如u=x+y,u=xy,u=x/y,u=1/yn等化为以上两种类型求解后再还原。
2、二阶常系数微分方程
 【1】
【1】
 【2】
【2】
【1】为齐次,【2】为非齐次。
2.1 齐次【1】的通解构造
![]() 为【1】的特征方程。
为【1】的特征方程。
(1)若特征方程有两个不同实根![]() 【1】通解为
【1】通解为
(2)若特征方程有重根 ![]() 【1】的通解为
【1】的通解为
(3)若特征方程有一对共轭复根![]() 【1】通解为
【1】通解为
2.2 非齐次【2】的通解
(1)若y*是【2】的一个特解,则【2】的通解为
(2)若y1*是 的一个特解,y2*
的一个特解,y2*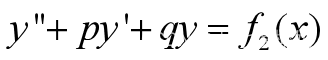 的一个特解,则微分方程
的一个特解,则微分方程 的通解为
的通解为
3、微分方程稳定性理论简介
3.1 一阶微分方程的平衡点及稳定性
 【3】
【3】
【3】的右端不含自变量t,称为自治方程,代数方程 f(x)=0的实根x=x0称为【1】的平衡点(奇点),它也是【1】的解(奇解)。
如果方程[3]的解从某个x(0)出发,满足  【4】
【4】
则称平衡点x0是稳定的,否则就不稳定。
若f(x)可微,则将f(x)在x0附近做一阶Taylor展开,则(1)就近似表达为 【5】
【5】
当x-x00时R1(x)是高阶无穷小。则[5]是【1】的近似线性方程,x0也是[5]的平衡点,关于x0的稳定性,有如下结论:
(1)若![]() x0对于【5】是稳定的;
x0对于【5】是稳定的;
(2)若![]() x0对于【5】是不稳定的;
x0对于【5】是不稳定的;
3.2 二元方程的平衡点及稳定性
 【6】
【6】
【6】右端不显含t,称为自治方程,方程组 【7】
【7】
的根x1=x10,x2=x20称为【6】的平衡点,记为p0(x10,x20).
如果 【8】
【8】
称p0为稳定的;否则称为不稳定的。
(1)线性常系数方程的稳定性讨论
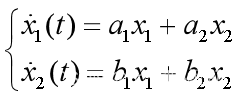 【9】
【9】
设【9】的系数矩阵为A,当|A|≠0时,【9】有唯一的平衡点p0(0,0)。若A有两个特征根
 【10】
【10】
(1*)若两个特征根都为负数或有负实部,则p0是平稳的;即p>0,q>0,平衡点稳定;
(2*)若两个特征根有一个为正或正实部,则p0是不稳定的。即p<0或q<0,平衡点不稳定;
(2)非线性二元方程,在p0(x10,x20)的稳定性讨论方法如下:

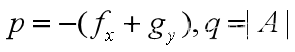
剩下的判断方法同上。










