目录
一、定义
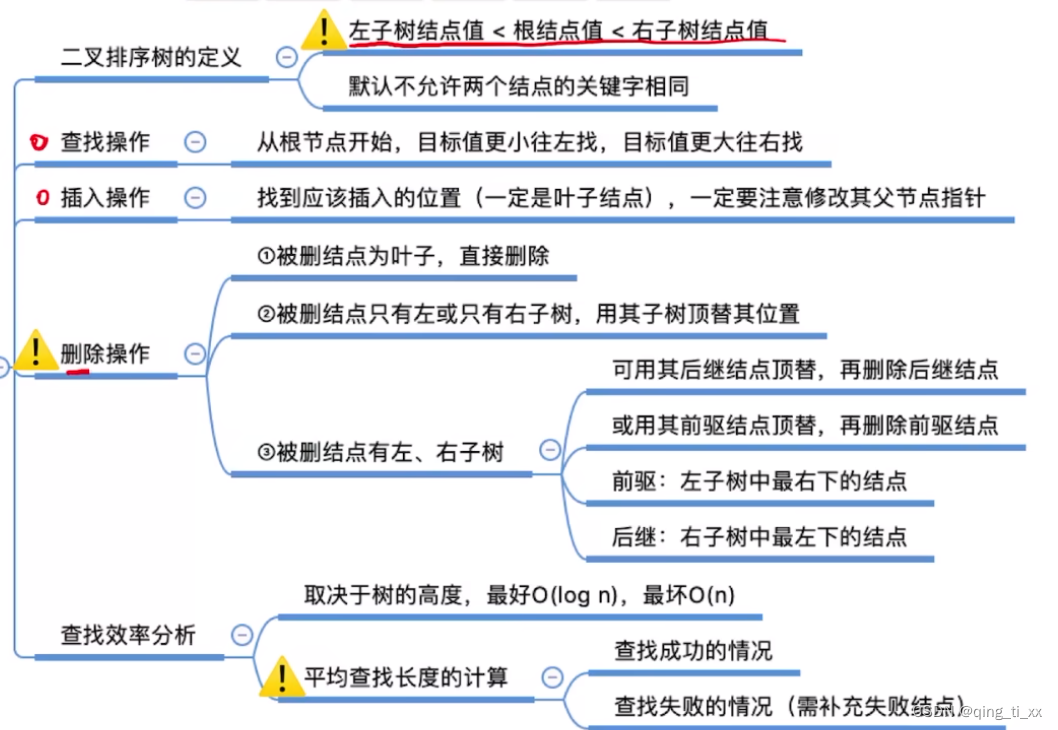
二叉排序树(Binary Search Tree,BST)是一种特殊的二叉树,它满足以下条件:
-
若左子树不为空,则左子树上所有节点的值(权值)均小于它的根节点的值;
-
若右子树不为空,则右子树上所有节点的值(权值)均大于它的根节点的值;
-
左、右子树本身也分别为二叉排序树。
二叉排序树的结构可以在查找、插入、删除操作中发挥重要作用,具有快速查找、插入、删除的特点。
二、代码实现
可以使用Binary Search Tree Visualization进行模拟测试。
1、查找
typedef struct TreeNode{
int data;
struct TreeNode *lchild,*rchild;
}TreeNode,*BTree;
TreeNode *BST_Search(BTree T,int e){
while(T!=NULL&&e!=T->data){
if (e>T->data){//大于
T = T->rchild;
} else{//小于
T = T->lchild;
}
}
return T;
}2、插入
//递归
int BST_Insert(BTree &T,int k){
if (T==NULL){
T=(BTree) malloc(sizeof(TreeNode));
T->data=k;
T->lchild=T->rchild=NULL;
return 1;//插入成功
} else if (k==T->data){
return 0;//已存在该值,插入失败
}
else if (k<T->data){
return (BST_Insert(T->lchild,k));//小于,插入左子树
} else{
return (BST_Insert(T->rchild,k));//大于,插入右子树
}
}
//非递归
int BST_Insert1(BTree &T,int k){
while(T!=NULL){
if (T->data == k){//存在该值
return 0;
}else if (T->data < k){//小于
if (T->lchild != NULL){//小于且不为叶子节点
T=T->lchild;
} else{//小于且为叶子节点
T->data=k;
T->lchild=T->rchild=NULL;
}
} else{//大于
if (T->rchild != NULL){//大于且不为叶子节点
T=T->rchild;
} else{//大于且为叶子节点
T->data=k;
T->lchild=T->rchild=NULL;
}
}
}
}3、构造
void Creat_Tree(BTree &T,int str[],int n){
T=NULL;
int i = 0;
while(i<n){
BST_Insert(T,str[i]);
i++;
}
}4、删除
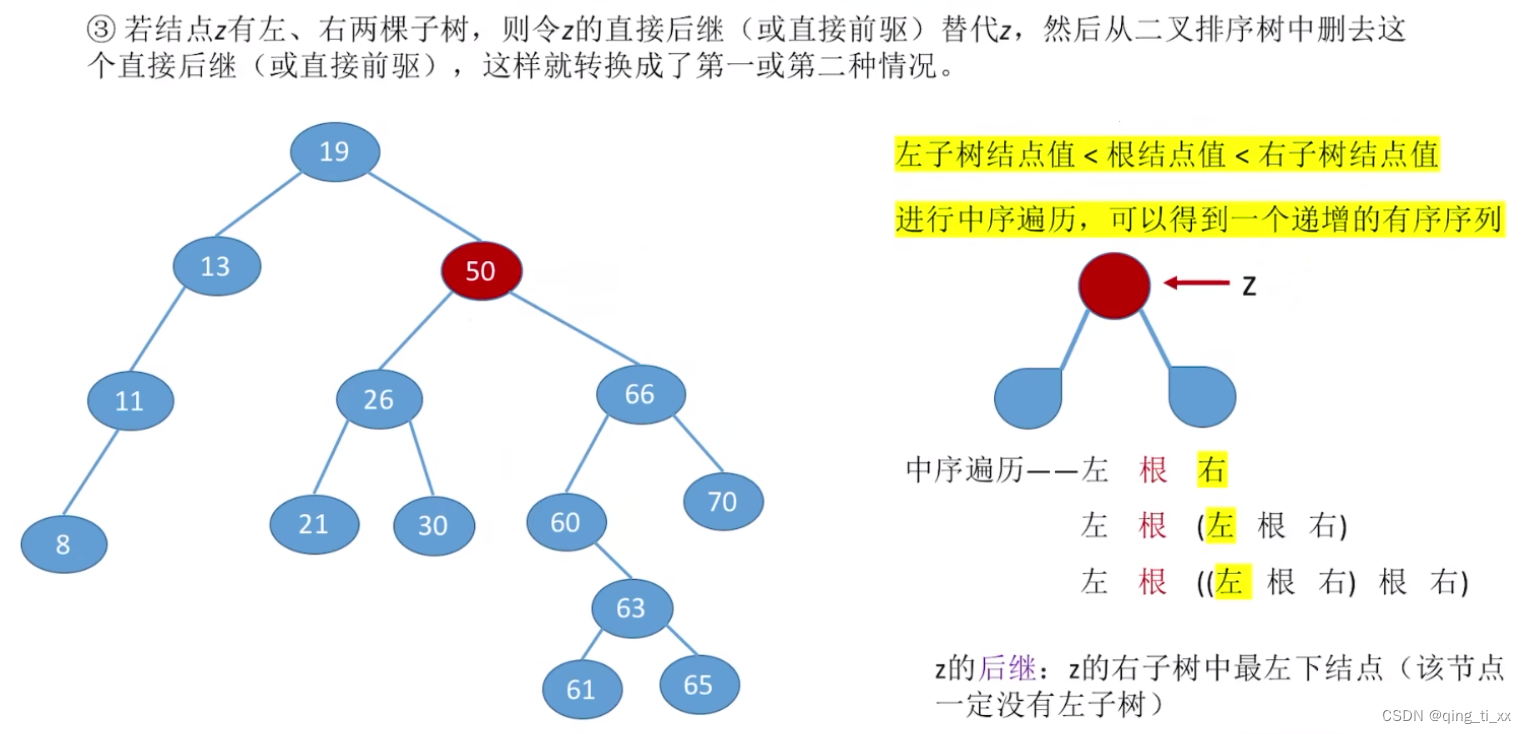
我们寻找代替被删除位置的结点时,有两种方案。
一种是找左子树中最大的值。(中序遍历最后访问的结点)
二是找右子树中最小的值。(中序遍历最先访问的结点)
三、查找效率分析
1、查找成功ASL
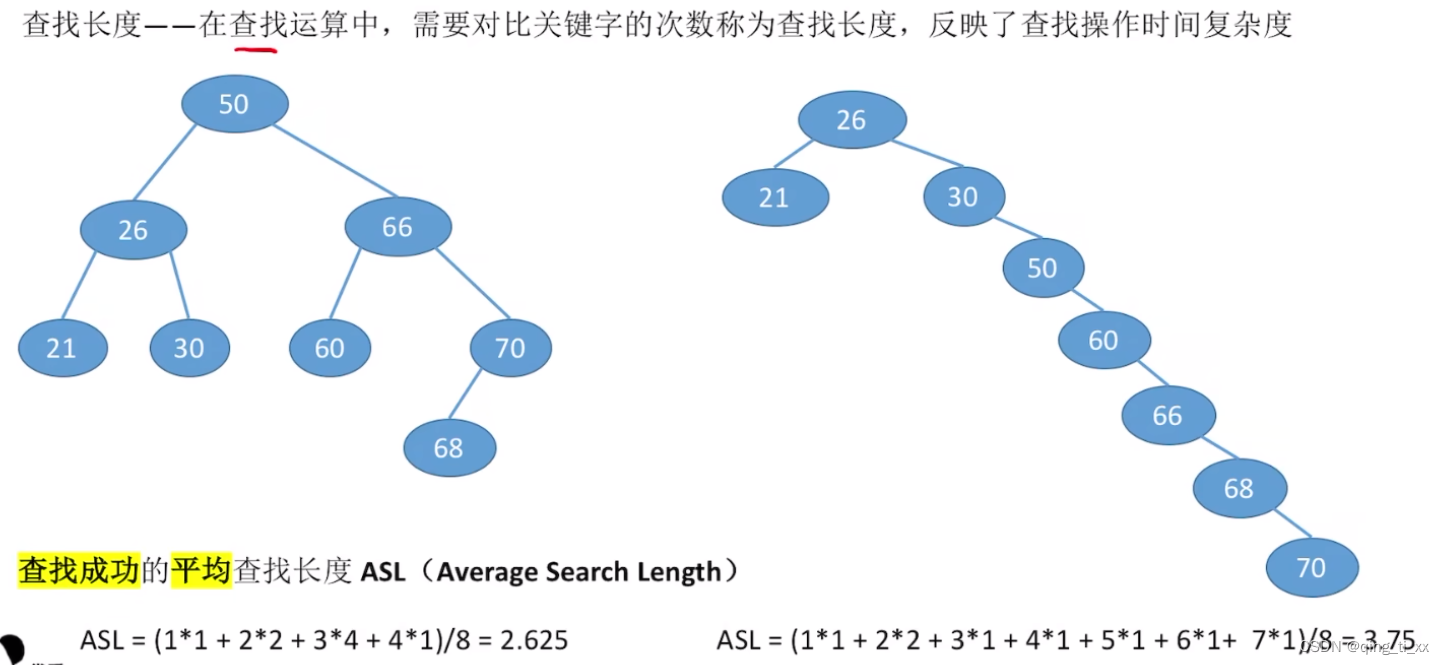
在上图中,
第一层的结点要查询一次;
第二层的结点要对比两次;
第三层的结点要对比三次;
第四层的结点要对比四次;
在乘以每层结点的个数,取平均值,就得到了查找成功的ASL;
2、查找失败ASL
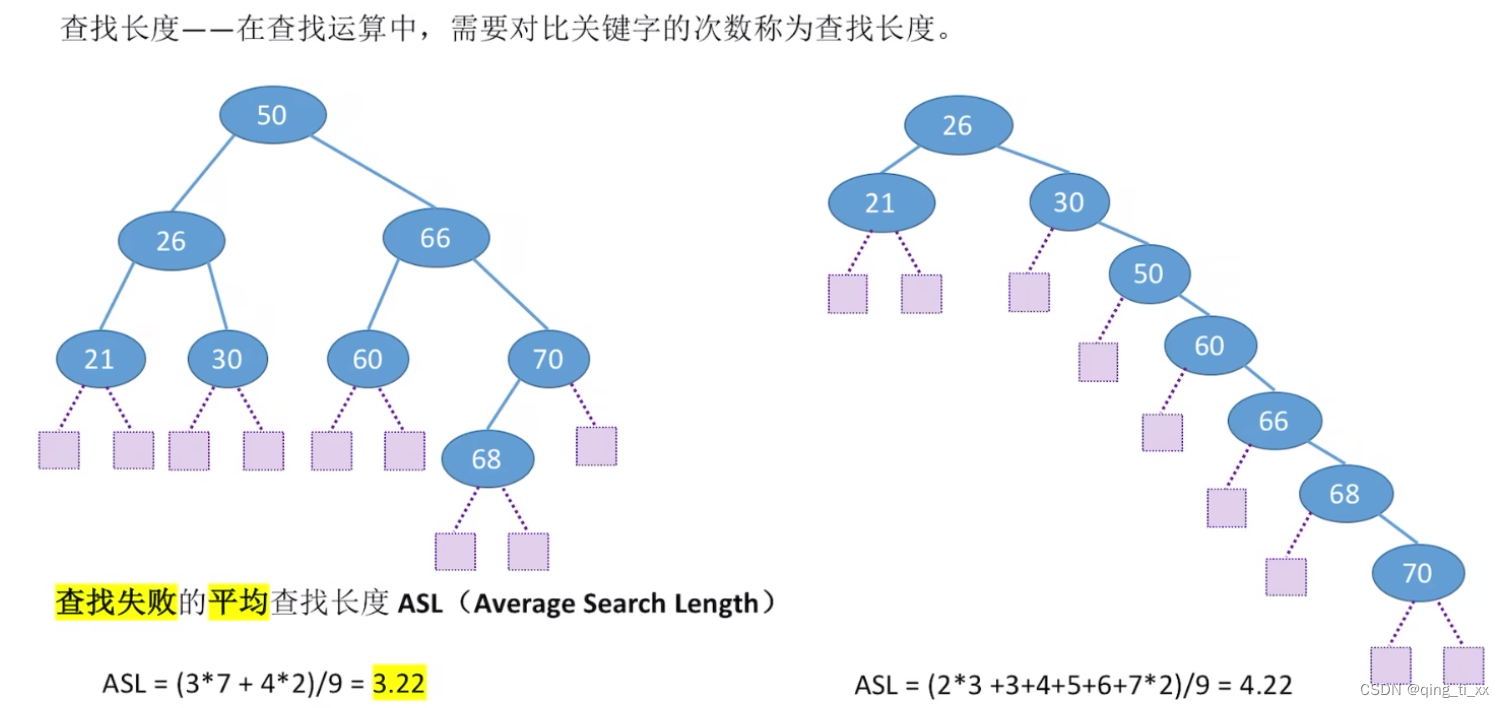
在上图中,
查找失败要对比三次的失败节点有7个;
查找失败要对比两次的失败节点有2个;
所以ASL为它们的平均值。
四、总结