130. 被围绕的区域
leetcode链接:题目链接
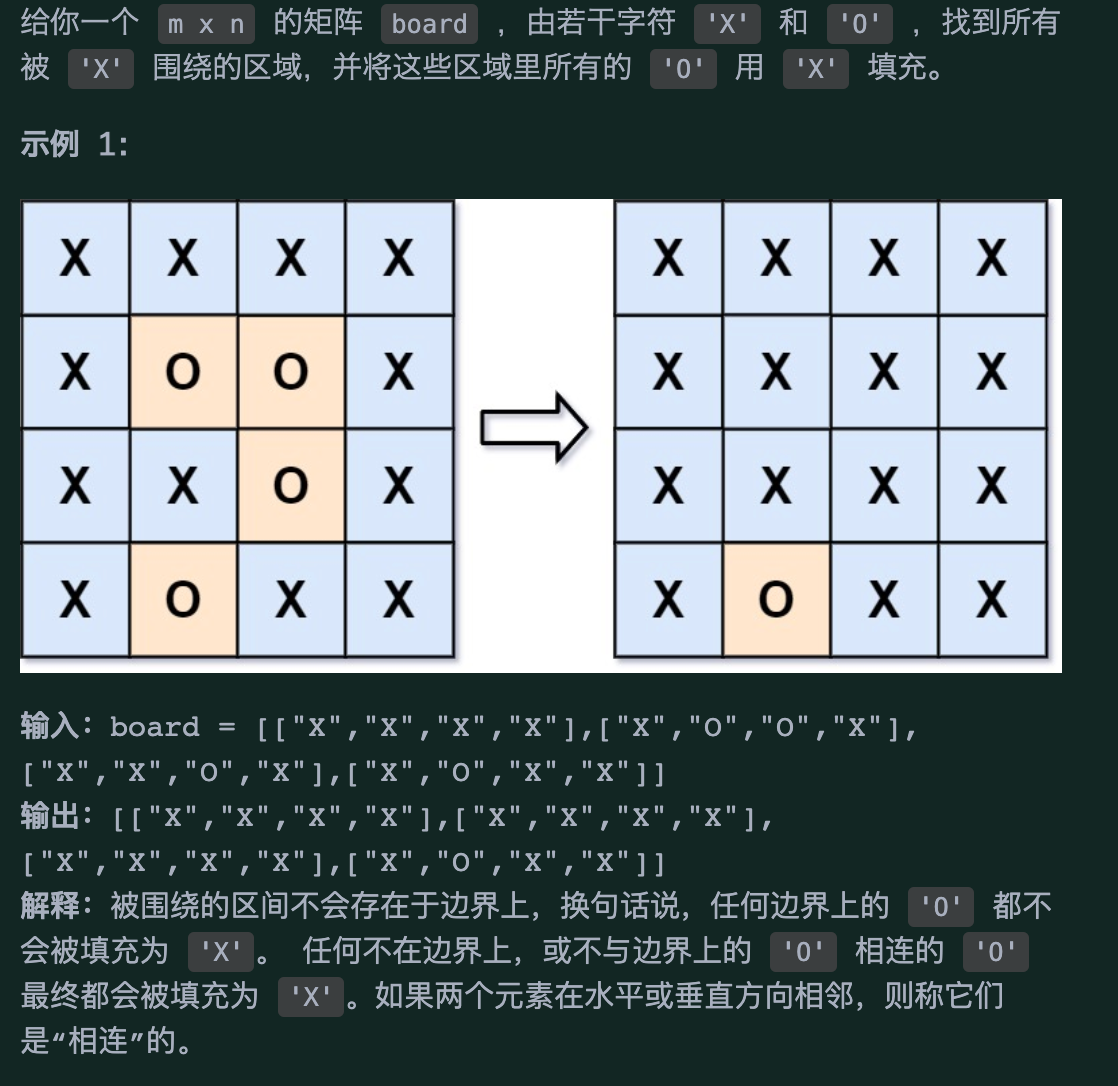
这题看起来很复杂,其实跟之前找飞地和找边缘地区的是差不多的,主要分三步:
- 使用dfs将边缘的岛都找出来,然后用A代替防止混淆;
- 再用dfs找中间不与任何岛相连的飞地;
- 最后把之前的A替换成O。
最终代码:
class Solution {
public:
void dfs(vector<vector<char>> &board, int i, int j, char ch){//找到o把其周围转化为ch
vector<int> dir = {0,-1,0,1,1,0,-1,0};
if(i < 0 || j < 0 || i >= board.size() || j >= board[0].size()){
return;
}
if(board[i][j] == 'X' || board[i][j] == 'a'){
return;
}
board[i][j] = ch;
for(int idx = 0; idx < 4; idx++){
dfs(board, i + dir[2 * idx], j + dir[2 * idx + 1],ch);
}
}
void solve(vector<vector<char>>& board) {
int m = board.size();
int n = board[0].size();
for(int i = 0; i < m; i++){
if(board[i][n - 1] == 'O'){
dfs(board,i, n - 1, 'a');
}
if(board[i][0] == 'O'){
dfs(board,i,0, 'a');
}
}
for(int j = 0; j < n; j++){
if(board[0][j] == 'O'){
dfs(board,0, j,'a');
}
if(board[m - 1][j] == 'O'){
dfs(board, m - 1, j,'a');
}
}
for(int i = 0; i < m; i++){
for(int j = 0; j < n;j++){
if(board[i][j] == 'O'){
board[i][j] = 'X';
}
if(board[i][j] =='a'){
board[i][j] = 'O';
}
}
}
// for(int i = 0; i < m; i++){
// for(int j = 0; j < n;j++){
// if(board[i][j] =='a'){
// board[i][j] = 'O';
// }
// }
// }
}
};
这里有几点注意的:
- dfs函数中,除了等于X需要return,等于A也需要return,否则递归就没办法结束。
- 只需要dfs淹没周围一圈的岛,中间的岛不用再dfs找了,直接替换就行,因为本题没有让我们以整个岛为单位做一些事情。
417. 太平洋大西洋水流问题
leetcode链接:题目链接

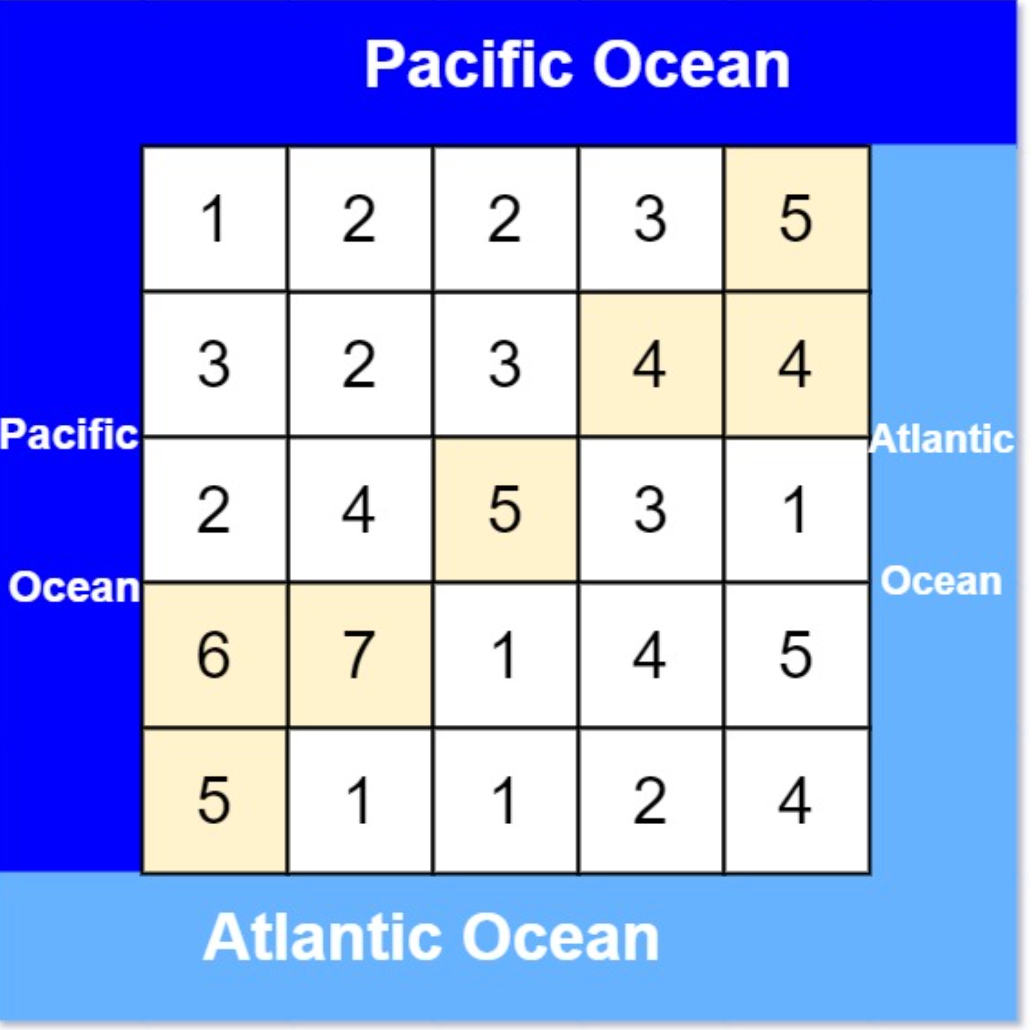
输入: heights = [[1,2,2,3,5],[3,2,3,4,4],[2,4,5,3,1],[6,7,1,4,5],[5,1,1,2,4]]
输出: [[0,4],[1,3],[1,4],[2,2],[3,0],[3,1],[4,0]]
示例 2:
输入: heights = [[2,1],[1,2]]
输出: [[0,0],[0,1],[1,0],[1,1]]
首先这题题目我都没怎么看懂,理解一下题意。
输入是一个二维数组,只要位于该点的值比四个方向的高就可以流向其他方向,最终既可以流向右边、下边(大西洋),又可以流向左边、上边(太平洋)的符合结果,输出result。
首先能想到一个很朴素的思路就是,对每个点都判断一下是否能同时流向大西洋和太平洋。这种思路的实现代码如下:
class Solution {
private:
int dir[4][2] = {-1, 0, 0, -1, 1, 0, 0, 1};
void dfs(vector<vector<int>>& heights, vector<vector<bool>>& visited, int x, int y) {
if (visited[x][y]) return;
visited[x][y] = true;
for (int i = 0; i < 4; i++) {
int nextx = x + dir[i][0];
int nexty = y + dir[i][1];
if (nextx < 0 || nextx >= heights.size() || nexty < 0 || nexty >= heights[0].size()) continue;
if (heights[x][y] < heights[nextx][nexty]) continue; // 高度不合适
dfs (heights, visited, nextx, nexty);
}
return;
}
bool isResult(vector<vector<int>>& heights, int x, int y) {
vector<vector<bool>> visited = vector<vector<bool>>(heights.size(), vector<bool>(heights[0].size(), false));
// 深搜,将x,y出发 能到的节点都标记上。
dfs(heights, visited, x, y);
bool isPacific = false;
bool isAtlantic = false;
// 以下就是判断x,y出发,是否到达太平洋和大西洋
for (int j = 0; j < heights[0].size(); j++) {
if (visited[0][j]) {
isPacific = true;
break;
}
}
for (int i = 0; i < heights.size(); i++) {
if (visited[i][0]) {
isPacific = true;
break;
}
}
for (int j = 0; j < heights[0].size(); j++) {
if (visited[heights.size() - 1][j]) {
isAtlantic = true;
break;
}
}
for (int i = 0; i < heights.size(); i++) {
if (visited[i][heights[0].size() - 1]) {
isAtlantic = true;
break;
}
}
if (isAtlantic && isPacific) return true;
return false;
}
public:
vector<vector<int>> pacificAtlantic(vector<vector<int>>& heights) {
vector<vector<int>> result;
// 遍历每一个点,看是否能同时到达太平洋和大西洋
for (int i = 0; i < heights.size(); i++) {
for (int j = 0; j < heights[0].size(); j++) {
if (isResult(heights, i, j)) result.push_back({i, j});
}
}
return result;
}
};
这种思路很直白,但很明显,以上代码超时了。 来看看时间复杂度。
遍历每一个节点,是 m * n,遍历每一个节点的时候,都要做深搜,深搜的时间复杂度是: m * n
那么整体时间复杂度 就是 O(m^2 * n^2) ,这是一个四次方的时间复杂度。
优化
那么我们可以 反过来想,从太平洋边上的节点 逆流而上,将遍历过的节点都标记上。 从大西洋的边上节点 逆流而长,将遍历过的节点也标记上。 然后两方都标记过的节点就是既可以流太平洋也可以流大西洋的节点。
class Solution {
private:
int dir[4][2] = {-1, 0, 0, -1, 1, 0, 0, 1}; // 保存四个方向
// 从低向高遍历,注意这里visited是引用,即可以改变传入的pacific和atlantic的值
void dfs(vector<vector<int>>& heights, vector<vector<bool>>& visited, int x, int y) {
if (visited[x][y]) return;
visited[x][y] = true;
for (int i = 0; i < 4; i++) { // 向四个方向遍历
int nextx = x + dir[i][0];
int nexty = y + dir[i][1];
// 超过边界
if (nextx < 0 || nextx >= heights.size() || nexty < 0 || nexty >= heights[0].size()) continue;
// 高度不合适,注意这里是从低向高判断
if (heights[x][y] > heights[nextx][nexty]) continue;
dfs (heights, visited, nextx, nexty);
}
return;
}
public:
vector<vector<int>> pacificAtlantic(vector<vector<int>>& heights) {
vector<vector<int>> result;
int n = heights.size();
int m = heights[0].size(); // 这里不用担心空指针,题目要求说了长宽都大于1
// 记录从太平洋边出发,可以遍历的节点
vector<vector<bool>> pacific = vector<vector<bool>>(n, vector<bool>(m, false));
// 记录从大西洋出发,可以遍历的节点
vector<vector<bool>> atlantic = vector<vector<bool>>(n, vector<bool>(m, false));
// 从最上最下行的节点出发,向高处遍历
for (int i = 0; i < n; i++) {
dfs (heights, pacific, i, 0); // 遍历最上行,接触太平洋
dfs (heights, atlantic, i, m - 1); // 遍历最下行,接触大西洋
}
// 从最左最右列的节点出发,向高处遍历
for (int j = 0; j < m; j++) {
dfs (heights, pacific, 0, j); // 遍历最左列,接触太平洋
dfs (heights, atlantic, n - 1, j); // 遍历最右列,接触大西洋
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
// 如果这个节点,从太平洋和大西洋出发都遍历过,就是结果
if (pacific[i][j] && atlantic[i][j]) result.push_back({i, j});
}
}
return result;
}
};
所以 调用dfs函数,只要参数传入的是 数组pacific,那么地图中 每一个节点其实就遍历一次,无论你调用多少次。
同理,调用 dfs函数,只要 参数传入的是 数组atlantic,地图中每个节点也只会遍历一次。
所以,以下这段代码的时间复杂度是 2 * n * m。 地图用每个节点就遍历了两次,参数传入pacific的时候遍历一次,参数传入atlantic的时候遍历一次。
827. 最大人工岛
leetcode链接:力扣链接
给你一个大小为 n x n 二进制矩阵 grid 。最多 只能将一格 0 变成 1 。
返回执行此操作后,grid 中最大的岛屿面积是多少?
岛屿 由一组上、下、左、右四个方向相连的 1 形成。
示例 1:
输入: grid = [[1, 0], [0, 1]]
输出: 3
解释: 将一格0变成1,最终连通两个小岛得到面积为 3 的岛屿。
示例 2:
输入: grid = [[1, 1], [1, 0]]
输出: 4
解释: 将一格0变成1,岛屿的面积扩大为 4。
示例 3:
输入: grid = [[1, 1], [1, 1]]
输出: 4
解释: 没有0可以让我们变成1,面积依然为 4。
先放这里放一下。题目居然是hard,不太想做岛屿类的题了,换换脑子。
总结
- 岛屿问题的dfs/bfs的代码基本大差不差,主要还是主函数中处理逻辑的问题;
- 学习带有 visited的dfs的写法。







