【算法】矩阵快速幂优化动态规划

2023-09-17 20:24:26

文章目录

知识讲解

矩阵快速幂可以将 O ( n ) O(n) O(n) 的 DP 优化成 O ( log ⁡ n ) O(\log{n}) O(logn) 的时间复杂度。

前置知识——快速幂，可见：【算法基础：数学知识】4.4 快速幂

我们拿递推公式 d p [ i ] = d p [ i − 1 ] + [ i − 2 ] dp[i] = dp[i - 1] + [i - 2] dp[i]=dp[i−1]+[i−2] 举例，
为了将其表示成矩阵乘法，添加一个式子 d p [ i − 1 ] = d p [ i − 1 ] dp[i - 1] = dp[i - 1] dp[i−1]=dp[i−1]
两个式子合并可以得——
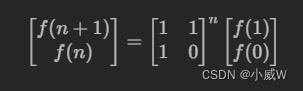
在这里插入图片描述
这是因为 d p [ i ] = 1 ∗ d p [ i − 1 ] + 1 ∗ [ i − 2 ] dp[i] = 1 * dp[i - 1] + 1 * [i - 2] dp[i]=1∗dp[i−1]+1∗[i−2] , d p [ i − 1 ] = 1 ∗ d p [ i − 1 ] + 0 ∗ [ i − 2 ] dp[i - 1] = 1 * dp[i - 1] + 0 * [i - 2] dp[i−1]=1∗dp[i−1]+0∗[i−2]

这样就可以对递推矩阵使用快速幂来将 n 次递推的时间复杂度简化到 logn。

题目列表

[矩阵快速幂] 题目列表📕

题目列表来源：https://leetcode.cn/problems/string-transformation/solutions/2435348/kmp-ju-zhen-kuai-su-mi-you-hua-dp-by-end-vypf/

70. 爬楼梯

https://leetcode.cn/problems/climbing-stairs/
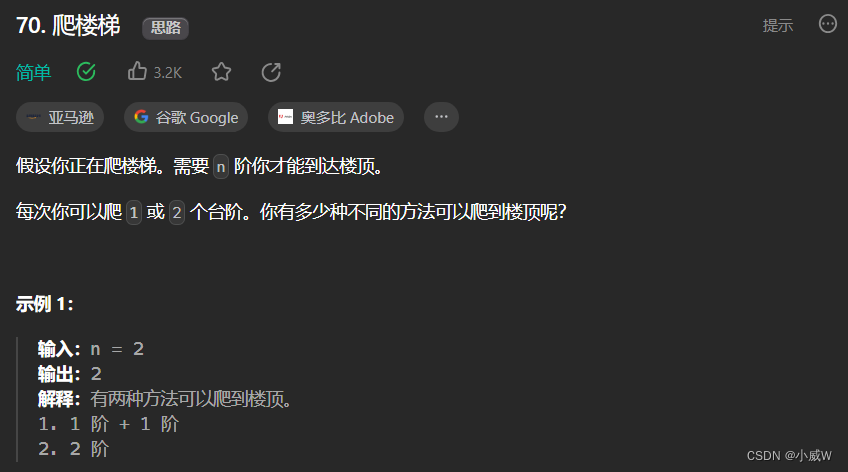
在这里插入图片描述

提示：
1 <= n <= 45

解法1——线性DP
class Solution {
    public int climbStairs(int n) {
        if (n <= 1) return n;
        int[] dp = new int[n];
        dp[0] = 1;
        dp[1] = 2;
        for (int i = 2; i < n; ++i) {
            dp[i] = dp[i - 1] + dp[i - 2];
        }
        return dp[n - 1];
    }
}
解法2——矩阵快速幂

根据递推公式，可以得出矩阵快速幂的矩阵是什么。

class Solution {
    public int climbStairs(int n) {
        if (n <= 2) return n;
        // m是根据递推公式来的
        int[][] m = {
            {1, 1},
            {1, 0}
        };
        return pow(m, n - 2)[0][0];
    }

    public int[][] pow(int[][] m, int k) {
        // dp[0] = 1,dp[1] = 2
        int[][] res = {
            {2, 0},
            {1, 0}
        };
        for (; k != 0; k /= 2) {
            if (k % 2 == 1) res = mul(m, res);
            m = mul(m, m);
        }
        return res;
    }

    public int[][] mul(int[][] x, int[][] y) {
        int[][] res = new int[2][2];
        for (int i = 0; i < 2; ++i) {
            for (int j = 0; j < 2; ++j) {
                res[i][j] = x[i][0] * y[0][j] + x[i][1] * y[1][j];
            }
        }
        return res;
    }
}

也可以更简洁一些，从 dp[0] 开始写，代码如下：

class Solution {
    public int climbStairs(int n) {
        // m是根据递推公式来的
        int[][] m = {
            {1, 1},
            {1, 0}
        };
        return pow(m, n)[0][0];
    }

    public int[][] pow(int[][] m, int k) {
        // dp[0] = 1
        int[][] res = {
            {1, 0},
            {0, 0}
        };
        for (; k != 0; k /= 2) {
            if (k % 2 == 1) res = mul(m, res);
            m = mul(m, m);
        }
        return res;
    }

    public int[][] mul(int[][] x, int[][] y) {
        int[][] res = new int[2][2];
        for (int i = 0; i < 2; ++i) {
            for (int j = 0; j < 2; ++j) {
                res[i][j] = x[i][0] * y[0][j] + x[i][1] * y[1][j];
            }
        }
        return res;
    }
}

509. 斐波那契数

https://leetcode.cn/problems/fibonacci-number/
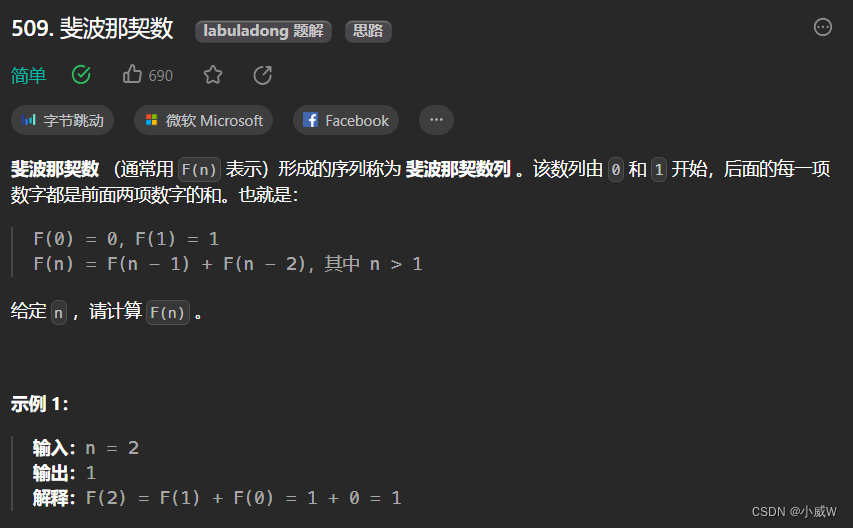
在这里插入图片描述
提示：
0 <= n <= 30

跟上一题差不多，注意初始值变了。

class Solution {
    public int fib(int n) {
        if (n == 0) return n;
        // m是根据递推公式来的
        int[][] m = {
            {1, 1},
            {1, 0}
        };
        return pow(m, n - 1)[0][0];
    }

    public int[][] pow(int[][] m, int k) {
        // dp[0] = 1
        int[][] res = {
            {1, 0},
            {0, 0}
        };
        for (; k != 0; k /= 2) {
            if (k % 2 == 1) res = mul(m, res);
            m = mul(m, m);
        }
        return res;
    }

    public int[][] mul(int[][] x, int[][] y) {
        int[][] res = new int[2][2];
        for (int i = 0; i < 2; ++i) {
            for (int j = 0; j < 2; ++j) {
                res[i][j] = x[i][0] * y[0][j] + x[i][1] * y[1][j];
            }
        }
        return res;
    }
}

1137. 第 N 个泰波那契数

https://leetcode.cn/problems/n-th-tribonacci-number/

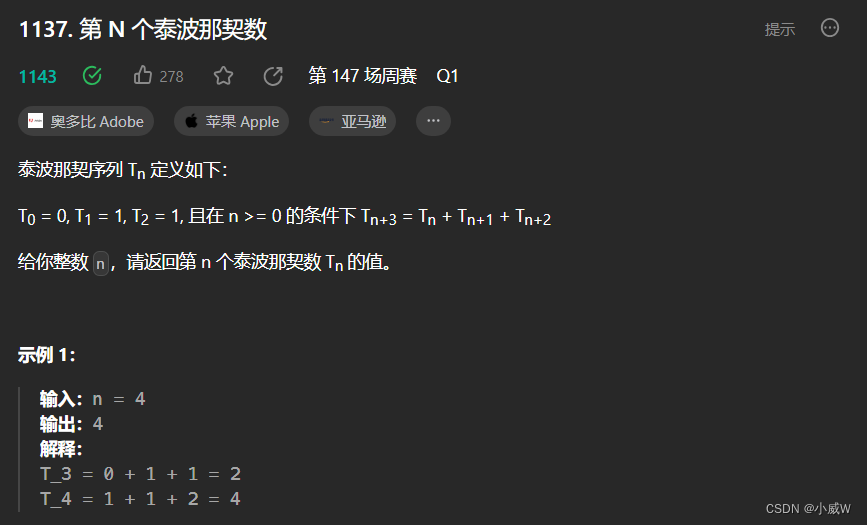
在这里插入图片描述
提示：
0 <= n <= 37
答案保证是一个 32 位整数，即 answer <= 2^31 - 1。

对矩阵稍作修改即可。

class Solution {
    public int tribonacci(int n) {
        if (n <= 1) return n;
        // m是根据递推公式来的
        int[][] m = {
            {1, 1, 1},
            {1, 0, 0},
            {0, 1, 0}
        };
        return pow(m, n - 2)[0][0];
    }

        public int[][] pow(int[][] m, int k) {
        // dp[0] = 0, dp[1] = 1, dp[2] = 1
        int[][] res = {
            {1, 0, 0},
            {1, 0, 0},
            {0, 0, 0}
        };
        for (; k != 0; k /= 2) {
            if (k % 2 == 1) res = mul(m, res);
            m = mul(m, m);
        }
        return res;
    }

    public int[][] mul(int[][] x, int[][] y) {
        int[][] res = new int[3][3];
        for (int i = 0; i < 3; ++i) {
            for (int j = 0; j < 3; ++j) {
                res[i][j] = x[i][0] * y[0][j] + x[i][1] * y[1][j] + x[i][2] * y[2][j];
            }
        }
        return res;
    }
}

1220. 统计元音字母序列的数目

https://leetcode.cn/problems/count-vowels-permutation/

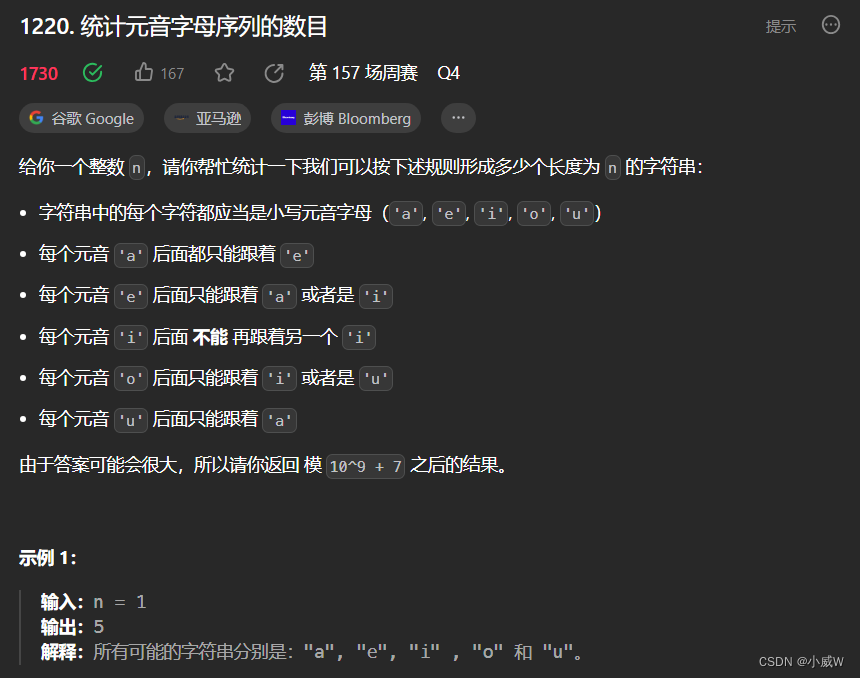
在这里插入图片描述

提示：
1 <= n <= 2 * 10^4

解法1——线性DP
class Solution {
    final long MOD = (int)1e9 + 7;
    public int countVowelPermutation(int n) {
        long[][] dp = new long[n][5];
        Arrays.fill(dp[0], 1);
        for (int i = 1; i < n; ++i) {
            dp[i][0] = dp[i - 1][1];
            dp[i][1] = (dp[i - 1][0] + dp[i - 1][2]) % MOD;
            dp[i][2] = (dp[i - 1][0] + dp[i - 1][1] + dp[i - 1][3] + dp[i - 1][4]) % MOD;
            dp[i][3] = (dp[i - 1][2] + dp[i - 1][4]) % MOD;
            dp[i][4] = dp[i - 1][0];
        }
        long ans = 0;
        for (long x: dp[n - 1]) ans = (ans + x) % MOD;
        return (int)ans;
    }
}
解法2——矩阵快速幂优化DP
class Solution {
    final long MOD = (int)1e9 + 7;

    public int countVowelPermutation(int n) {
        long[][] m = {
            {0, 1, 0, 0, 0},
            {1, 0, 1, 0, 0},
            {1, 1, 0, 1, 1},
            {0, 0, 1, 0, 1},
            {1, 0, 0, 0, 0}
        };
        long[][] res = pow(m, n - 1);
        long ans = 0;
        for (int i = 0; i < 5; ++i) ans = (ans + res[i][0]) % MOD;
        return (int)ans;
    }

    public long[][] pow(long[][] m, int k) {
        long[][] res = {
            {1, 0, 0, 0, 0},
            {1, 0, 0, 0, 0},
            {1, 0, 0, 0, 0},
            {1, 0, 0, 0, 0},
            {1, 0, 0, 0, 0}
        };
        for (; k != 0; k /= 2) {
            if (k % 2 == 1) res = mul(m, res);
            m = mul(m, m);
        }
        return res;
    }

    public long[][] mul(long[][] x, long[][] y) {
        long[][] res = new long[5][5];
        for (int i = 0; i < 5; ++i) {
            for (int j = 0; j < 5; ++j) {
                res[i][j] = (x[i][0] * y[0][j] + x[i][1] * y[1][j] + x[i][2] * y[2][j] + x[i][3] * y[3][j] + x[i][4] * y[4][j]) % MOD;
            }
        }
        return res;
    }
}

552. 学生出勤记录 II（🚹递归公式 & 矩阵快速幂优化🐂）

https://leetcode.cn/problems/student-attendance-record-ii/
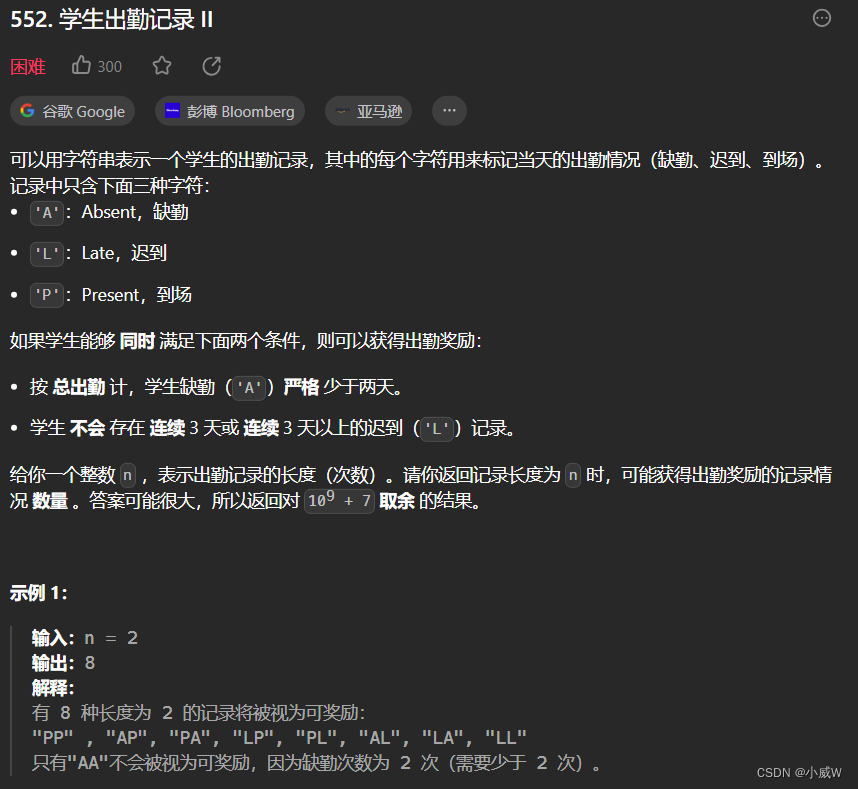
在这里插入图片描述
提示：
1 <= n <= 10^5

解法1——动态规划
class Solution {
    final int MOD = (int)1e9 + 7;

    public int checkRecord(int n) {
        // 长度，A 的数量，结尾连续 L 的数量
        int[][][] dp = new int[n + 1][2][3];    
        dp[0][0][0] = 1;
        for (int i = 1; i <= n; ++i) {
            // 以P结尾
            for (int j = 0; j < 2; ++j) {
                for (int k = 0; k < 3; ++k) {
                    dp[i][j][0] = (dp[i][j][0] + dp[i - 1][j][k]) % MOD;
                }
            }
            // 以A结尾
            for (int k = 0; k < 3; ++k) {
                dp[i][1][0] = (dp[i][1][0] + dp[i - 1][0][k]) % MOD;
            }
            // 以L结尾
            for (int j = 0; j < 2; ++j) {
                for (int k = 1; k < 3; ++k) {
                    dp[i][j][k] = (dp[i][j][k] + dp[i - 1][j][k - 1]) % MOD;
                }
            }
        }

        int ans = 0;
        for (int j = 0; j < 2; ++j) {
            for (int k = 0; k < 3; ++k) {
                ans = (ans + dp[n][j][k]) % MOD;
            }
        }
        return ans;
    }
}
解法2——矩阵快速幂优化DP（TODO）
在这里插入代码片

790. 多米诺和托米诺平铺⭐（🚹想出递推公式）

https://leetcode.cn/problems/domino-and-tromino-tiling/
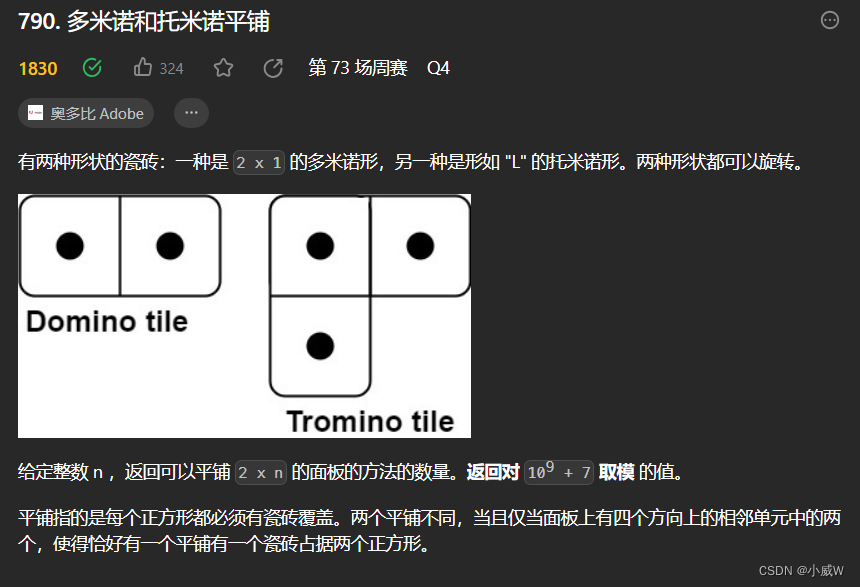
在这里插入图片描述
提示：
1 <= n <= 1000

解法1——动态规划1 分最后一列的状态

https://leetcode.cn/problems/domino-and-tromino-tiling/solutions/1962465/duo-mi-nuo-he-tuo-mi-nuo-ping-pu-by-leet-7n0j/
在这里插入图片描述

class Solution {
    final int MOD = (int)1e9 + 7;

    public int numTilings(int n) {
        // 0空，1上，2下，3满
        int[][] dp = new int[n][4];
        dp[0][0] = dp[0][3] = 1;
        for (int i = 1; i < n; ++i) {
            dp[i][0] = dp[i - 1][3];
            dp[i][1] = (dp[i - 1][0] + dp[i - 1][2]) % MOD;
            dp[i][2] = (dp[i - 1][0] + dp[i - 1][1]) % MOD;
            dp[i][3] = (((dp[i - 1][0] + dp[i - 1][1]) % MOD + dp[i - 1][2]) % MOD + dp[i - 1][3]) % MOD;
        }
        return dp[n - 1][3];
    }
}
解法2——动态规划2 列出式子找通项公式（TODO 还没想明白）

https://leetcode.cn/problems/domino-and-tromino-tiling/solutions/1968516/by-endlesscheng-umpp/
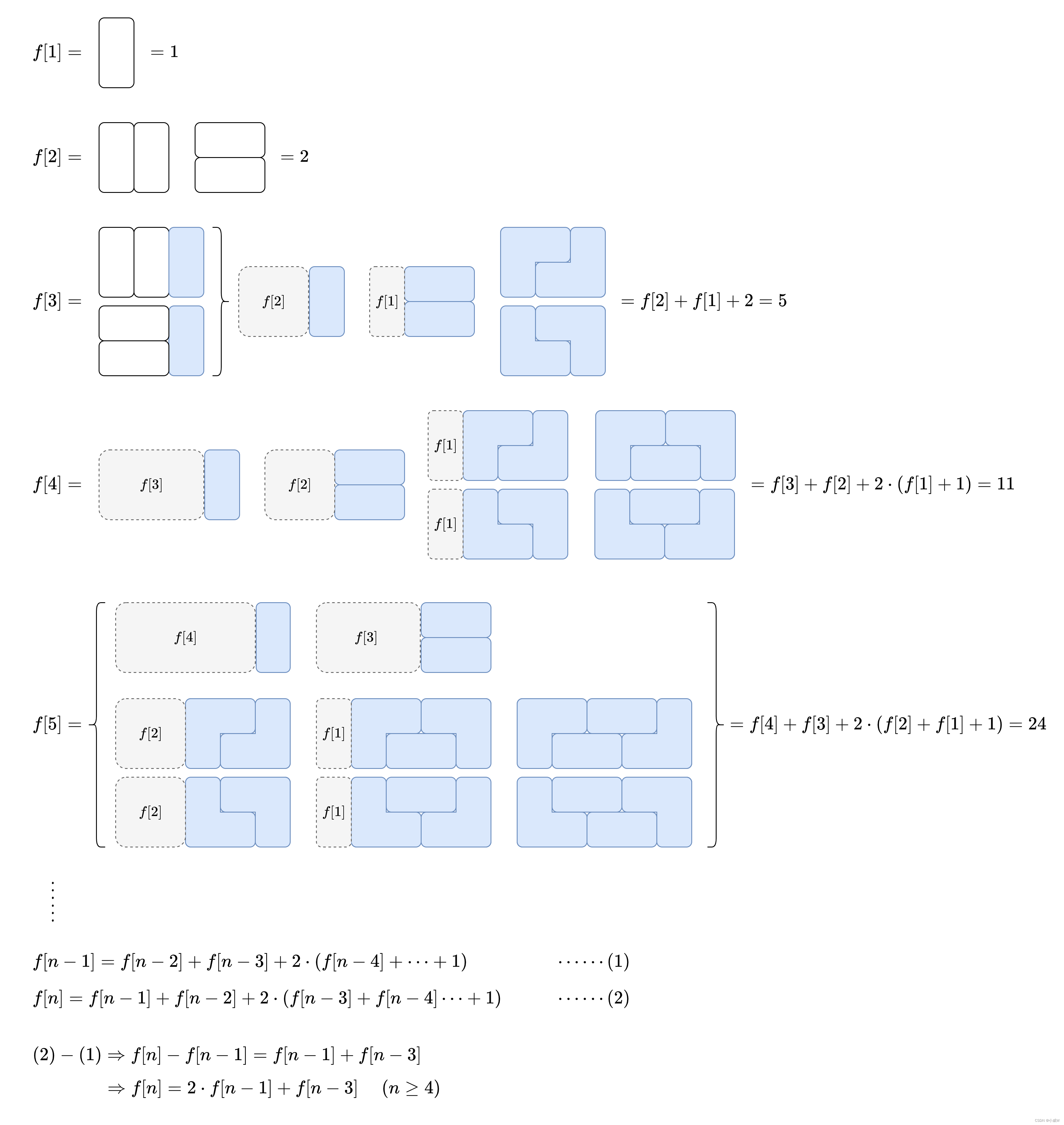
在这里插入图片描述

class Solution {
    final long MOD = (long)1e9 + 7;

    public int numTilings(int n) {
        if (n <= 2) return n;
        long[] dp = new long[n + 1];
        dp[0] = 1;
        dp[1] = 1;
        dp[2] = 2;
        for (int i = 3; i <= n; ++i) {
            dp[i] = (dp[i - 1] * 2 + dp[i - 3]) % MOD;
        }
        return (int)dp[n];
    }
}
解法3——矩阵快速幂优化DP
class Solution {
    final int MOD = (int)1e9 + 7;

    public int numTilings(int n) {
        // 0空，1上，2下，3满
        long[][] m = {
            {0, 0, 0, 1},
            {1, 0, 1, 0},
            {1, 1, 0, 0},
            {1, 1, 1, 1}
        };
        return (int)pow(m, n - 1)[3][0];
    }

    public long[][] pow(long[][] m, int k) {
        long[][] res = {
            {1, 0, 0, 0},
            {0, 0, 0, 0},
            {0, 0, 0, 0},
            {1, 0, 0, 0}
        };
        for (; k != 0; k >>= 1) {
            if ((k & 1) == 1) res = mul(m, res);
            m = mul(m, m);
        }
        return res;
    }

    public long[][] mul(long[][] a, long[][] b) {
        long[][] c = new long[4][4];
        for (int i = 0; i < 4; ++i) {
            for (int j = 0; j < 4; ++j) {
                c[i][j] = (a[i][0] * b[0][j] + a[i][1] * b[1][j] + a[i][2] * b[2][j] + a[i][3] * b[3][j]) % MOD;
            }
        }
        return c;
    }
}
# 相关链接
[【力扣周赛】第 362 场周赛（⭐差分&匹配&状态压缩DP&矩阵快速幂优化DP&KMP）](https://blog.csdn.net/qq_43406895/article/details/132824604)
更多推荐

解决vue项目导出当前页Table为Excel

解决vue项目中导出当前页表格为Excel表格的方案用到的技术：Vue2Element-uifile-saverxlsx1、创建vue项目，安装element-ui2、创建一个组件，组件内放入表格，和导出按钮<template><div><!--导出的按钮--><el-buttonsize="small"type="p

SpringSecurity

SpringSecurity从入门到精通参考代码0.简介​SpringSecurity是Spring家族中的一个安全管理框架。相比与另外一个安全框架Shiro，它提供了更丰富的功能，社区资源也比Shiro丰富。​一般来说中大型的项目都是使用SpringSecurity来做安全框架。小项目有Shiro的比较多，因为相比与

深入JavaScript的运行原理

一、深入V8引擎原理1.JavaScript代码的执行JavaScript代码下载好之后，是如何一步步被执行的呢？我们知道，浏览器内核是由两部分组成的，以webkit为例：WebCore：负责HTML解析、布局、渲染等等相关的工作；JavaScriptCore：解析、执行JavaScript代码；另外一个强大的Java

邮件营销中为什么要细分联系人？

在电子商务行业，邮件营销成为了各大企业吸引客户、推广产品的主要方式之一。然而，有效进行邮件营销需要一套完善的联系人管理系统。本文将从以下五点详细探讨邮件营销联系人管理有必要吗？一、精确定位目标用户邮件营销联系人管理是通过收集、分析和管理用户信息的过程。通过建立一个详尽的联系人数据库，企业可以对客户进行细致的分类和分组。

计算机网络第五节 网络层

一，网络引入的目的1.网络层以下层次解决的问题，未解决的问题从7层结构上看，网络层下是数据链路层从4层结构上看，网络层下面是网络接口层至少我们看到的网络层下面是以太网以太网解决了什么问题？答：以太网解决了具体网络上主机间数据传输的问题；主机之间可以以物理地址，以广播的传输方式进行数据的交换传输没有解决人心不足答的问题：

Springboot定时任务 Spring task

文章目录SpringTask简单操作SpringBoot注解开始1.fixDelay2.fixedRate单线程3.fixedRate多线程4.initialDelay5.cron（推荐）6.任务调度配置SpringTask简单操作SpringBoot注解开始@EnableScheduling@SpringBootAp

【JavaEE】多线程（三）

多线程（三）续上文，多线程（二），我们已经讲了创建线程Thread的一些重要的属性和方法那么接下来，我们继续来体会了解多线程吧~文章目录多线程（三）线程启动startstart与run的区别中断线程interrupt方法一方法二线程等待join线程状态线程安全线程安全问题的原因synchronized线程启动start

Scrum敏捷开发企业培训大纲介绍-企业内训

课程简介Scrum是目前运用最为广泛的敏捷开发方法，是一个轻量级的项目管理和产品研发管理框架。这是一个两天的实训课程，面向研发管理者、项目经理、产品经理、研发团队等，旨在帮助学员全面系统地学习Scrum和敏捷开发,帮助企业快速启动敏捷实施。课程采用案例讲解＋沙盘演练的方式授课，通过两天的强化训练学员将学会基于Scrum

Java笔记：JVM优化分析

1.我们为什么要对jvm做优化？在本地开发环境中我们很少会遇到需要对jvm进行优化的需求，但是到了生产环境，我们可能将有下面的需求：运行的应用“卡住了”，日志不输出，程序没有反应服务器的CPU负载突然升高在多线程应用下，如何分配线程的数量？……说明：使用的jdk版本为1.8。2.jvm的运行参数在jvm中有很多的参数可

iOS 17中的Safari配置文件改变了游戏规则，那么如何设置呢

Safari在iOS17中最大的升级是浏览配置文件——能够在一个应用程序中创建单独的选项卡和书签组。这些也可以跟随你的iPad和Mac，但在本指南中，我们将向你展示如何使用运行iOS17的iPhone。你可能有点困惑，为什么Safari中没有明显的位置可以添加个人资料，我们当然也是。诀窍是，你需要先在“设置”中添加配置

docker day04

Dockerfile:-FORM:1.指定基础镜像，可以起别名，也可以指定多个FROM指令，用于多阶段构建;2.加载触发器，加载ONBUILD指令;3.不指定基础镜像，声明当前镜像不依赖任何镜像，官方保留字:scratch-RUN:1.在容器中运行命令，同一个Dockerfile中可以有多个RUN指令并不会被覆盖;-C

热文推荐
  1. avformat_find_stream_info 为什么总是等到超时或超过大小才退出?

    avformat_find_stream_info为什么总是等到超时或超过大小才退出?/*author:hjjdebug*date:2023年09月21日星期四11:05:56CST*description:avformat_find_stream_info为什么不能正常退出了？*/查文档：mpegts:scan_al

  2. Java版工程行业管理系统源码-专业的工程管理软件- 工程项目各模块及其功能点清单

    鸿鹄工程项目管理系统SpringCloud+SpringBoot+Mybatis+Vue+ElementUI+前后端分离构建工程项目管理系统1.项目背景一、随着公司的快速发展，企业人员和经营规模不断壮大。为了提高工程管理效率、减轻劳动强度、提高信息处理速度和准确性，公司对内部工程管理的提升提出了更高的要求。二、企业通过

  3. 学信息系统项目管理师第4版系列09_配置管理

    1.配置管理1.1.应用技术的和管理的指导和监控方法以标识和说明配置项的功能和物理特征，控制这些特征的变更，记录和报告变更处理和实现状态并验证与规定的需求的遵循性1.1.1.GB/T11457《信息技术软件工程术语》2.配置项2.1.ConfigurationItem,CI2.2.为配置管理设计的硬件、软件或二者的集合

  4. 停车场系统、智慧城市停车、智慧社区、物业管理、新能源充电、人脸门禁 uniapp 系统源码

    1.智慧停车支持模式封闭性单个停车场路边停车(车位级管理)大小场(场中场)，多场子并行或嵌套所有者模式统一平台管理总平台下子账号(区域代理)自建场地资源，自行维护数据总平台下子账号(区域代理)再分配和单个停车场管理人员(物业管理/维保/保安/财务等人员)场站管理【车位控制】精准的实时车位统计和数据及时推送到场地led/

  5. 智汇云舟入选《2023全国企业数字化应用优秀解决方案》报告

    &nbsp;&nbsp;&nbsp;&nbsp;近日，由中国国际数字经济博览会组委会主办，中关村数字经济产业联盟、河北省数字经济联合会、衡水市人民政府共同承办的2023中国国际数字经济博览会首届全国企业数字化应用生态大会在石家庄举行。会上重磅发布了《2023全国企业数字化应用场景与解决方案》研究报告，智汇云舟“视频孪生

  6. Vue中的路由懒加载：提高性能和用户体验

    Vue中的路由懒加载：提高性能和用户体验在现代Web应用程序中，性能和用户体验是至关重要的。为了加速页面加载速度和提高用户感知的响应性，Vue提供了一种路由懒加载的方法。本文将详细介绍Vue中如何进行路由懒加载，并提供代码示例来演示如何实现它。什么是路由懒加载？路由懒加载是一种技术，它允许您将Vue路由的组件按需加载。

  7. 安卓内存优化案例穷举

    安卓内存优化是一个很重要的话题，有很多方面可以考虑，比如避免内存泄漏、减少内存抖动、优化图片加载、使用缓存和对象池等。下面我举一些代码案例，分别展示不合适的写法和高性能的写法。欢迎评论区留言指正和补充。1.避免使用枚举类型。枚举类型会占用更多的内存，因为它是一个类对象，而不是一个基本类型。如果需要定义一些常量，可以使用

  8. 【Python】pyecharts 模块 ① ( ECharts 简介 | pyecharts 简介 | pyecharts 中文网站 | pyecharts 画廊网站 | pyecharts 画 )

    文章目录一、pyecharts模块1、ECharts简介2、pyecharts简介3、pyecharts中文网站4、pyecharts画廊网站5、pyecharts画廊用法pyecharts画廊网站:https://gallery.pyecharts.org/#/一、pyecharts模块1、ECharts简介ECha

  9. u盘内容防止复制（U盘内数据防拷贝的方法）

    随着科技的发展，U盘已经成为我们日常生活和工作中不可或缺的一部分。然而，U盘的普及也带来了一些问题，如数据泄露、病毒传播等。因此，保护U盘中的数据安全变得尤为重要。方法一：设置文件权限打开U盘，找到需要保护的文件或文件夹。右键点击文件或文件夹，选择“属性”。在弹出的属性窗口中，切换到“安全”选项卡。点击“编辑”按钮，打