文章目录
Sudoku(数独)是一种基于逻辑的数字填充谜题游戏,最受喜爱的是那些热爱逻辑和推理的人。解决数独谜题有助于提高集中注意力和逻辑思维能力。
本文介绍了如何使用Python解决数独谜题。
使用回溯算法在Python中解决数独
在寻找计算问题的解决方案时,我们经常使用回溯算法。在解决数独时,它检查已填充的格子的数字是否有效。
如果数字无效,它会检查从1到9的其他数字。如果找不到有效数字,它将回溯到前一个选项。
当我们遇到死胡同并返回到先前的选择时,我们已经做出了一个选择并将更改我们的选择,从而得到一个不同的可能解。
让我们采用实现数独求解器和回溯算法的方法。
首先,我们需要通过形成谜题来设置数独板。
def setBoardFunc(puz):
global grid
print('\n---------------数独求解器---------------\n')
print('数独问题如下:')
for i in range(0, len(puz), 9):
row = puz[i:i+9]
temp = []
for block in row:
temp.append(int(block))
grid.append(temp)
printGridFunc()
在这里,我定义了一个名为setBoardFunc()的函数来形成数独谜题。在循环过程中,它设置一个9x9的谜题,并用0初始化空单元格。
完成函数操作后,它打印出给定的输入。然后我们需要打印出数独格局;这一步打印出带有给定输入的9x9格局。
def printGridFunc():
global grid
for row in grid:
print(row)
接下来,我们将检查当前值是否可以放置在当前格子中。
def checkValidFunc(row,column,num):
global grid
for i in range(0,9):
if grid[row][i] == num:
return False
for i in range(0,9):
if grid[i][column] == num:
return False
square_row = (row//3)*3
square_col = (column//3)*3
for i in range(0,3):
for j in range(0,3):
if grid[square_row+i][square_col+j] == num:
return False
return True
这一步检查给定的数字是否适用于特定的格子。该数字不能是同一行、同一列或同一块中的任何其他格子。
如果数字满足该要求并返回true,则可以移动到下一个值;否则,该数字被拒绝。然后我们必须遍历所有块来适应回溯算法。
def solveFunc():
global grid
for row in range(9):
for column in range(9):
if grid[row][column] == 0:
for num in range(1,10):
if checkValidFunc(row,column,num):
grid[row][column] = num
solveFunc()
grid[row][column] = 0
return
print('\n数独问题的解决方案:')
printGridFunc()
代码的后半部分检查数字是否有效。在这里,它引入了回溯算法。
首先,它搜索空单元格;如果找到了,说明已经解决了数独,它打印出给定数独的解决方案。如果找到任何空格,它将通过迭代从1到9猜测一个数字。
如果存在有效数字,则调用 solveFunc() 并移动到下一个空单元格,但如果没有有效的猜测,函数的先前调用将将单元格的值重置为0并继续迭代以找到下一个有效数字。
当算法使用有效数字填充空格直到死胡同时,它会回溯过程并重新迭代整个过程。最后,让我们传递数独格局并调用函数来解决给定的数独谜题。
puz = "004300209005009001070060043006002087190007400050083000600000105003508690042910300"
grid = []
setBoardFunc(puz)
solveFunc()
完整的源代码:
def setBoardFunc(puz):
global grid
print('\n---------------数独求解器---------------\n')
print('数独问题如下:')
for i in range(0, len(puz), 9):
row = puz[i:i+9]
temp = []
for block in row:
temp.append(int(block))
grid.append(temp)
printGridFunc()
def printGridFunc():
global grid
for row in grid:
print(row)
def checkValidFunc(row,column,num):
global grid
for i in range(0,9):
if grid[row][i] == num:
return False
for i in range(0,9):
if grid[i][column] == num:
return False
square_row = (row//3)*3
square_col = (column//3)*3
for i in range(0,3):
for j in range(0,3):
if grid[square_row+i][square_col+j] == num:
return False
return True
def solveFunc():
global grid
for row in range(9):
for column in range(9):
if grid[row][column] == 0:
for num in range(1,10):
if checkValidFunc(row,column,num):
grid[row][column] = num
solveFunc()
grid[row][column] = 0
return
print('\n数独问题的解决方案:')
printGridFunc()
puz = "004300209005009001070060043006002087190007400050083000600000105003508690042910300"
grid = []
setBoardFunc(puz)
solveFunc()
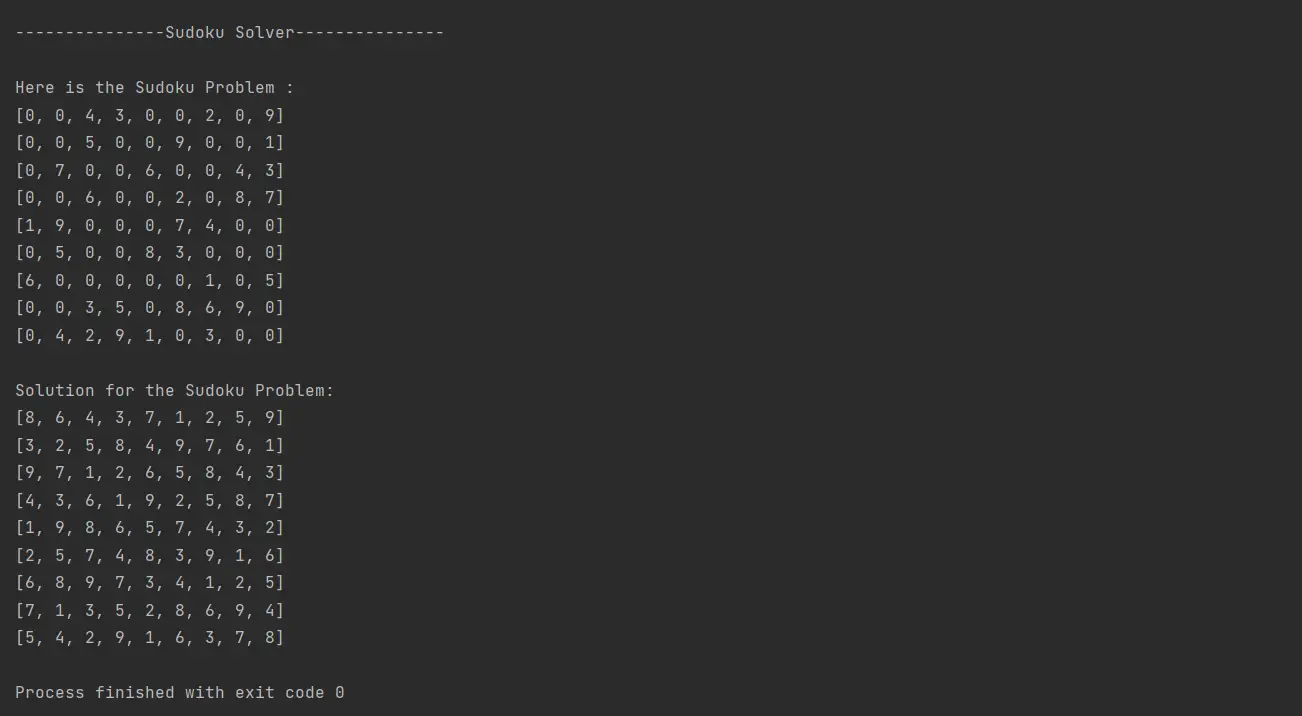
输出:
总结
尽管还有其他解决方法,但使用回溯算法可以得到数独问题更准确的最终解,但它需要更多时间,因为其中包含许多迭代。然而,解决数独谜题可以提高一个人的逻辑思维能力,并且是一种有趣的消遣方式。








