对于图像分类任务，模型最终是通过softmax操作输出一个概率分布向量的（各个类别和为1）

假设我们有三类别 [ 小车，小牛，小火箭 ]，假设有两张图片，分别有两个模型来对这两张图片分别预测 ，我们将真实标签转换为概率分布——独热码，如下图所示

假设两个模型经过训练后输出概率分布如下图

比如模型一对图片一火箭的预测为 [0.3,0.3,0.4 ] 说明模型认为图片是小车的概率是0.3，小牛的概率是0.3，小火箭的概率是0.4 ，最大的概率值便是最后的预测——小火箭

所以

模型一对图片一，二的预测分别为 火箭 和 小牛

模型二对图片 一，二的预测也分别为 火箭和 小牛

1.损失函数原理

1.1 Classification Error（分类错误率）

如果我们以图片错误率作为损失函数

$\frac{预测错误数}{图片总数}$

模型一二都预测对一张图片，预测错一张图片

那么模型一二 的损失都为0.5，这样无法区分两个模型的好坏

但实际上对于图片一，模型一预测小火箭的概率很低0.4 而模型二预测很高0.9，我们更期望模型二这样的情况出现

1.2. 均方差损失

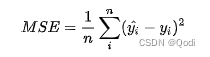
模型一

​ 图片一

$(0.3-0{)}^2+(0.3-0{)}^2+(0.4-1{)}^2=0.54$

​ 图片二

$(0.1-1{)}^2+(0.8-0{)}^2+(0.1-0{)}^2=1.46$

$MSE=\frac{0.54+1.46}{2}=1$

模型二

​ 图片一

$(0.1-0{)}^2+(0.1-0{)}^2+(0.9-1{)}^2=0.03$

​ 图片二

$(0.4-1{)}^2+(0.5-0{)}^2+(0.1-0{)}^2=0.62$

$MSE=\frac{0.03+0.62}{2}=0.325$

我们发现，MSE能够判断出来模型2优于模型1，那为什么不采样这种损失函数呢？在分类中更多采用交叉熵损失函数呢

（1）在分类问题中，我们通常希望模型的输出概率分布尽可能地接近真实标签的概率分布，而交叉熵损失函数可以直接衡量这种差异。相比之下，MSE损失函数只能衡量模型输出和标签之间的距离，无法直接反映概率分布的差异。

（2）交叉熵损失函数对于模型的误差敏感度更高。在分类问题中，误差大部分发生在模型输出概率最大的那个类别上，而交叉熵损失函数在这种情况下的梯度更大，可以更快地更新模型参数，从而提高模型的准确性。相比之下，MSE损失函数在这种情况下的梯度相对较小，更新速度更慢。

1.3 交叉熵损失函数

1.3.1 数学原理

假设存在两个概率分布 P,Q

注意这里的log是以e为底

熵： $H(p)=-{\sum }_{x}p(x)logp(x)$

熵是信息论中用于衡量随机变量不确定性的指标，它表示一个随机变量的平均信息量。熵越大，表示随机变量的不确定性越大，即信息量越大。例如$[0,0,1]$这个分布没啥信息量，因为他的不确定度很小

我们通过上面公式计算一下他的熵会发现为0

而对于分布[0.3,0.3.0.4]这个分布不确定性比较大，熵值就更大了

相对熵：$KL(p||q)=-{\sum }_{x}p(x)log\frac{q(x)}{p(x)}$

相对熵，也叫KL散度用来度量两个分布的不相似性（这里不叫做距离，是因为距离的话P到q和q到p的距离应该是一样的）而这里的话有可能不一样

如果两个分布一样，则相对熵为0，如果两个分布差异越大，相对熵越大

比如分布P[0,0,1]为和分布Q为 [0.3,0.3,0.4] 的相对熵为0.39，说明他俩相差比较大

而分布P为[0,0,1]和分布Q为 [0,0.1,0.9]相对熵0.04.说明他俩相差较小

实际中用到更多的是交叉熵

交叉熵： $H(p,q)=-{\sum }_{x}p(x)logq(x)$

因为三者存在这样一个关系

$H(p,q)=H(p)+KL(p||q)$

而如果P分布是标答，分布是独热码的形式，那么它的H§ 就等于0 ，这样的话，我们就可以用交叉熵来代表相对熵了，计算更简单

再代入计算刚刚的交叉熵损失函数

模型一

注意这里的log是以e为底

​ 图片一

$-(0\ast log(0.3)+0\ast log(0.3)+1\ast log(0.4))=-log(0.4)=0.9163$

​ 图片二

$-(1\ast log(0.1)+0\ast log(0.8)+0\ast log(0.1))=-log(0.1)=2.3026$

模型二

​ 图片一

$-(0\ast log(0.1)+0\ast log(0.1)+1\ast log(0.9))=-log(0.9)=0.1054$

​ 图片二

$-(1\ast log(0.4)+0\ast log(0.5)+0\ast log(0.1))=-log(0.4)=0.9163$

明显 模型二损失更低，要优于模型一

1.3.2 代码实现

观察发现实际输出就是真实标签概率的负对数

所以用pytorch库来一句话简单实现

import torch
#第一个模型对两张图片的预测
y_hat=torch.tensor([[0.3,0.3,0.4],[0.1,0.8,0.1]])
#真实标签 2代表第3类小火箭，0代表第1类小车
y=torch.tensor([2,0])  
def cross_entropy(y_hat,y):
    return -torch.log(y_hat[range(len(y_hat)),y])
print(cross_entropy(y_hat,y))

可能会对y_hat[range(len(y_hat)),y]操作比较迷糊，我当时也是这样的

这里参考李沐老师的动手深度学习，我们没有用for循环进行计算，而是用了索引，会更加高效，具体如下：

1. y_hat[range(len(y_hat)),y]：对 y_hat 进行了索引操作，其中 y 是一个一维张量，包含了两个整数，用于选取每行中的一个元素。

   具体来说，range(len(y_hat)) 表示一个从 0 到 1 的整数序列，对应于 y_hat 中的两行，而 y 则表示选取每行中的一个元素的下标。因此，这个表达式的含义是选取 y_hat 中每行中下标为 y 的元素，返回一个一维张量。

当然，实际中，我们更多使用高级API

nn.CrossEntropyLoss

可以一步计算Softmax和交叉熵损失，同时可以解决溢出等问题