官方链接:https://ww2.mathworks.cn/help/images/ref/cp2tform.html?s_tid=doc_ta.
cp2tform函数的作用是根据传入的控制点对的坐标推断空间变换参数。
函数语法如下:
从控制点对推断空间变换,并将此变换作为tform结构返回,有些转换类型具有可选的富家参数transformationType,比如下面的语法所示
tform = cp2tform(movingPoints, fixedPoints, transformationType)
指定要使用的多项式的顺序进行空间变换
tform = cp2tform(movingPoints, fixedPoints, 'polynomial', degree)
通过使用相邻控制点在每个控制点推断多项式来创建映射。任何位置的映射都取决于这些多项式的加权平均值,可以选择用于推断每个多项式的点数n,n个最接近的点用于推断每个控制点对的2阶多项式
tform = cp2tform(movingPoints, fixedPoints, 'lwm', n));
创建固定控制点的Delaunay三角测量,并将相应的移动控制点映射到固定控制点。映射对于每个三角形是线性当设的,并且在控制点上是连续的,但由于每个三角形都有自己的映射,所以不连续可微
tform = cp2tform(movingPoints, fixedPoints, 'piecewise linear')
在usedMP和usedFP中返回用于分段线性变换的控制点,还在badMP和badFP中返回被相处的控制点,因为它们是退化折叠三角形的重点顶点
[tform, usedMP, usedFP, badMP, badFP] = cp2tform(movingPoints, fixedPoints, 'piecewise linear')
使用cpstruct结构来存储运动图像和固定运动图像的控制点坐标
tform = cp2tform(cpstruct, transformationType,____)
在usedMP和usedFP中返回用于转换的控制点,不使用不匹配点和预测点。
[tform, usedMP, usedFP] = cp2tform(cpstruct, transformationType, ____)
参数说明:
输入参数:
movingPoints:要配准或运动图像中的控制点,指定为 m × 2 m \times 2 m×2矩阵,每一行指定一个控制点的[x y]坐标,数据类型为double类型。示例:[11 11; 41 71]。fixedPoints:基准或固定图像中的控制点,指定为 m × 2 m \times 2 m×2矩阵,每一行指定一个控制点的[x y]坐标,数据类型为double类型。示例:[14 44; 70 81]。tranformationType:转换类型,指定为以下类型之一,按复杂性增加的顺序列出。cp2tform函数需要最小数量的控制点对来推断每个变换类型的结构。
表1-转换类型及其说明
| 转换类型 | 描述 | 控制点对的最小数量 |
|---|---|---|
nonreflective similarity | 非反射相似性, 当运动图像中的形状不变时,但图像因平移、旋转和缩放的某些组合而失真时,请使用此变换。直线保持直线,平行线仍然平行 | 2 |
similarity | 与添加可选反射的非反射性相似相同 | 3 |
affine | 当输入图像中的形状展示出错效果使用本变换。变换后直线仍然是直线,平行线仍为平行线,但矩形变成了平行四边形 | 3 |
projective | 当场景显得倾斜时使用本变换,变换后直线仍然为直线,但平行线不再平行 | 4 |
polynomial | 当图像中的对象发生弯曲时使用本变换。拟合中选用的多项式的阶数越高,拟合效果越好,但配准后的图像比基准图像包含更多的曲线,同时也需要更多的基准点对 | 6-二阶 10-三阶 15-四阶 |
piecewise linear | 当图像呈现分段变形现象时使用本变换 | 4 |
lwm | 当图像中的变形具有局部化特点,并且分段线性条件不够充分时考虑使用本变换 | 6,建议12 |
cpstruct:余弦选定的控制点,指定为一个结构,cpstruct中包含关于运动图像和固定图像中所有控制点的x和y做白哦的信息,包括未配对和预测的控制点。cpstruct2pairs函数消除不匹配和预测的控制点,并返回一组有效的控制点对。cpstruct是控制点选择工具在选择将点到处到工作区选项时生成的结构。degree:多项式变换的次数,指定为整数2、3、4,可以是matlab支持的数值类型。n:在局部加权平均值计算中使用的点数,指定为正整数,n可以小到6,但使n小有生成病态多项式的风险。
输出参数:
tform:TFORM结构,作为TFORM结构返回;usedMP:用于推断空间变换的移动控制点,以 n × 2 n \times 2 n×2的矩阵的形式返回,不使用不匹配点和预测点;usedFP:用于推断空间变换的固定控制点,以 n × 2 n \times 2 n×2的矩阵形式返回,不使用不匹配点和预测点;badMP:由于被确定为异常值而被消除的移动控制点,以 p × 2 p \times 2 p×2的矩阵形式返回;badFP:固定的控制点由于被确定为异常值而被消除,并以 p × 2 p \times 2 p×2的矩阵形式返回;
使用示例
使用控制点创建无反射相似性转换结构
%% cp2tform 函数获取图像转换结构
clc; close all; format compact;
I = checkerboard; % 加载棋盘格图片
J = imrotate(I, 30); % 逆时针旋转30°
figure;
subplot(1,2,1); imshow(I, []); title('原始图片');
subplot(1,2,2); imshow(J, []); title('逆时针旋转30°');
fixedPoints = [11 11; 41 71]; % 固定控制点对
movingPoints = [14 44; 70 81]; % 移动控制点对
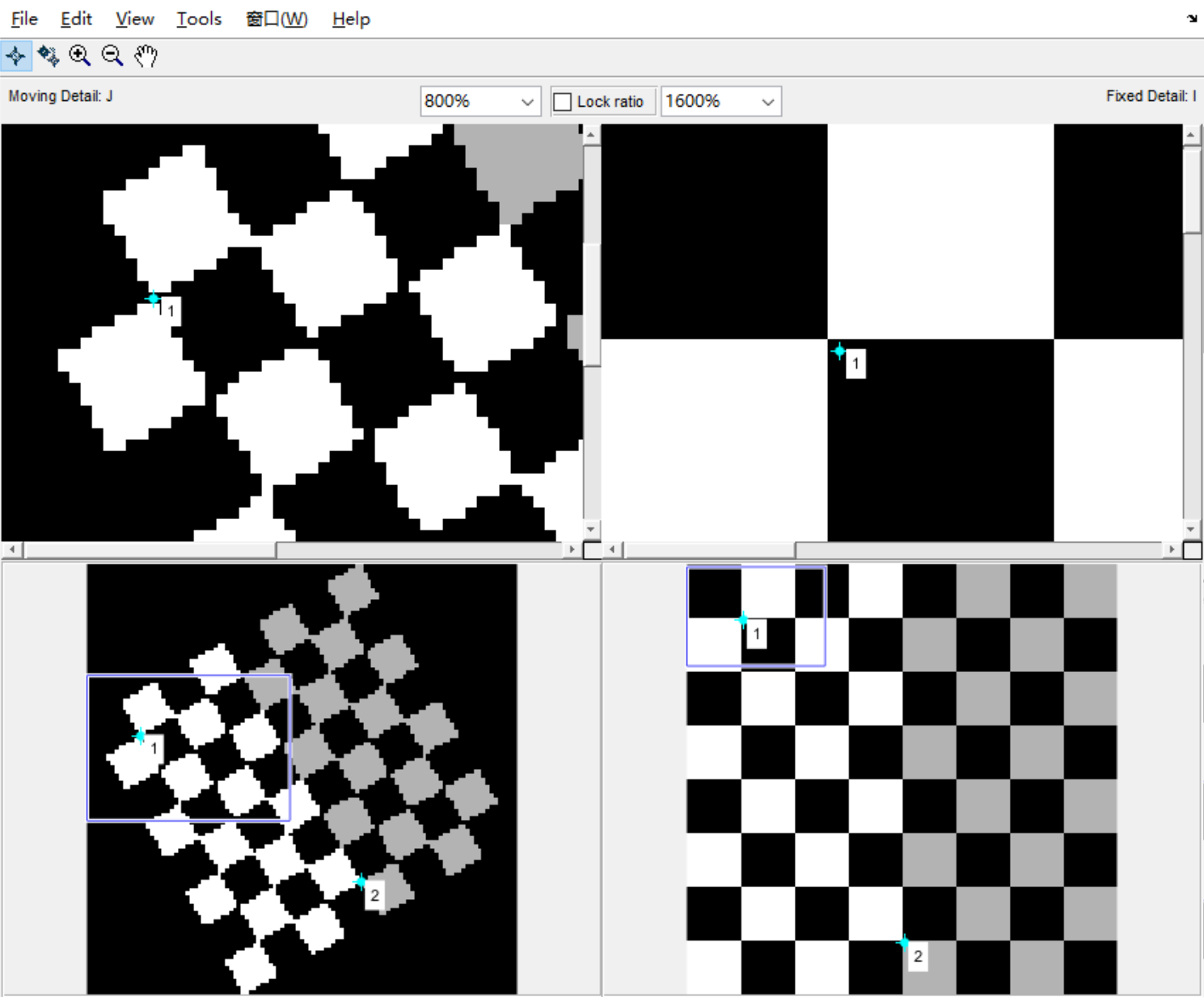
cpselect(J, I, movingPoints, fixedPoints);
% 获取非反射相似性变换,使用cp2tform函数返回变换,
% 并将tform的角度和和比例与原始变换的角度和规模进行比较
t = cp2tform(movingPoints, fixedPoints, 'nonreflective similarity');
% 使用一组有效的移动和固定控制点对启动控制点选择工具,可以以交互式添加控制点
% 通过检查平行于x轴的单位向量的旋转和拉伸方式,恢复角度和比例
u = [0 1];
v = [0 0];
[x y] = tformfwd(t, u, v); % 将t中的空间变换作用于u和v,将结果返回给x和y
dx = x(2) - x(1);
dy = y(2) - y(1);
angle = (180 / pi) * atan2(dy, dx)
scale = 1 / sqrt(dx ^2 + dy^2)
显示结果:
angle =
29.9816
scale =
1.0006