目录标题
参考学习链接
计算机视觉与深度学习-04-图像去噪&卷积-北邮鲁鹏老师课程笔记
什么是图像边缘?
图像中亮度明显而急剧变化的点
为什么研究边缘?
1 编码图像中的语义与形状信息。
2 相对于像素表示,边缘表示显然更加紧凑。
有哪些边缘种类?
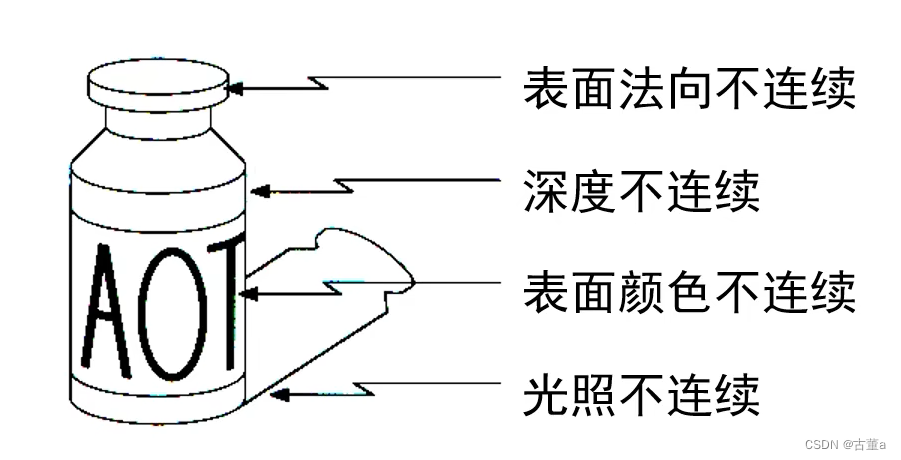
表面法向不连续
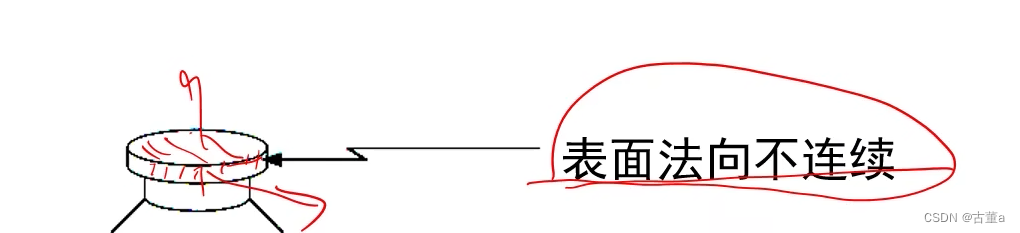
瓶盖上方的法线向上,瓶盖周围的法线向外。
深度不连续
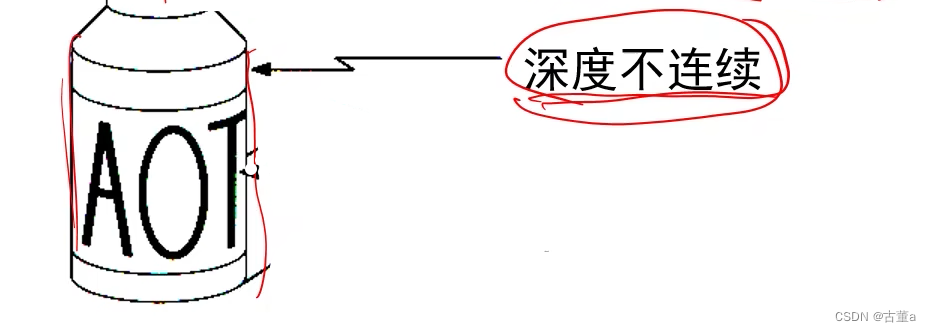
真实图片中是不存在的,拍照照到的地方和照不到的地方的边界。
表面颜色不连续
如这几个AOT字母产生的边

识别物体时需考虑,品牌标签等
光照不连续
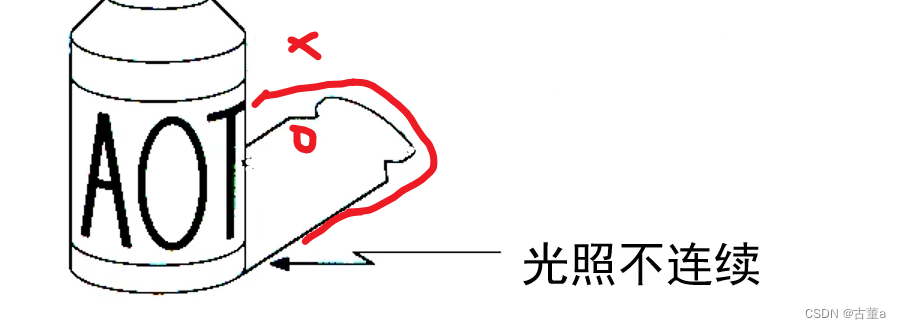
感知物体位置时需要考虑,与周围物体的位置关系。例如:阴影。
如何检测边缘?
边缘处的导数取最值
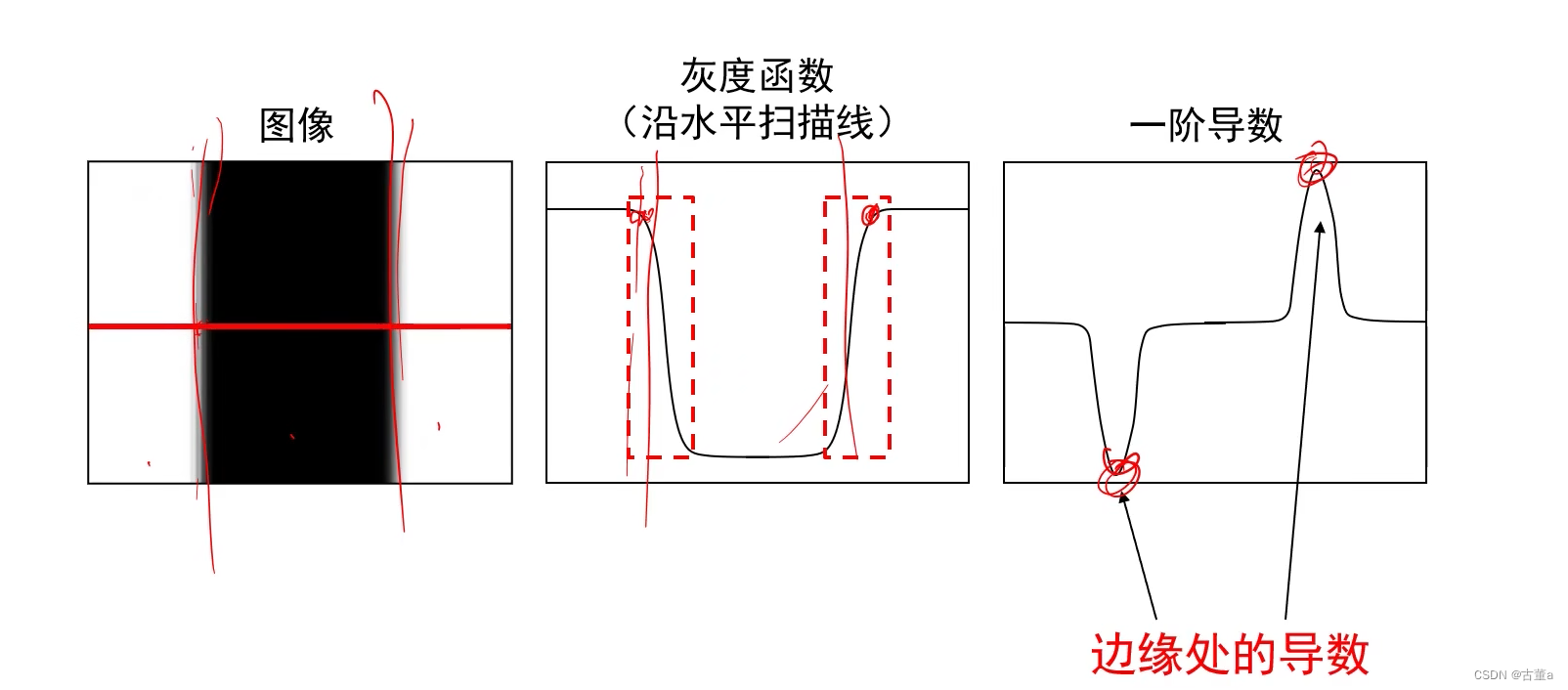
图像求导
2D函数f(x,y)的偏导为:
- 对x的偏导
∂ f ∂ x = lim ε → 0 f ( x + ε , y ) − f ( x , y ) ε \frac{{\partial f}}{{\partial x}}=\lim_{{\varepsilon \to 0}} \frac{{f(x + \varepsilon, y) - f(x, y)}}{{\varepsilon}} ∂x∂f=ε→0limεf(x+ε,y)−f(x,y) - 对y的偏导
∂ f ( x , y ) ∂ x = lim ε → 0 f ( x , y + ε ) − f ( x , y ) ε \frac{{\partial f(x,y)}}{{\partial x}}=\lim_{{\varepsilon \to 0}} \frac{{f(x, y + \varepsilon) - f(x, y)}}{{\varepsilon}} ∂x∂f(x,y)=ε→0limεf(x,y+ε)−f(x,y)
图像求导公式
将2D函数中求偏导公式中邻域范围改成1,得到的效果还可以。所以一直沿用。
∂
f
(
x
,
y
)
∂
x
≈
f
(
x
+
1
,
y
)
−
f
(
x
,
y
)
1
\frac{{\partial f(x,y)}}{{\partial x}} \approx \frac{{f(x + 1, y) - f(x, y)}}{{1}}
∂x∂f(x,y)≈1f(x+1,y)−f(x,y)
由上图中图像求导公式可知:
图像求导公式
=
右边像素
f
(
x
+
1
,
y
)
−
自己
f
(
x
,
y
)
图像求导公式 = 右边像素 f(x + 1,y) - 自己f(x,y)
图像求导公式=右边像素f(x+1,y)−自己f(x,y)
因此,图像求导可以通过卷积核实现。

举例,对图像使用高斯核进行卷积

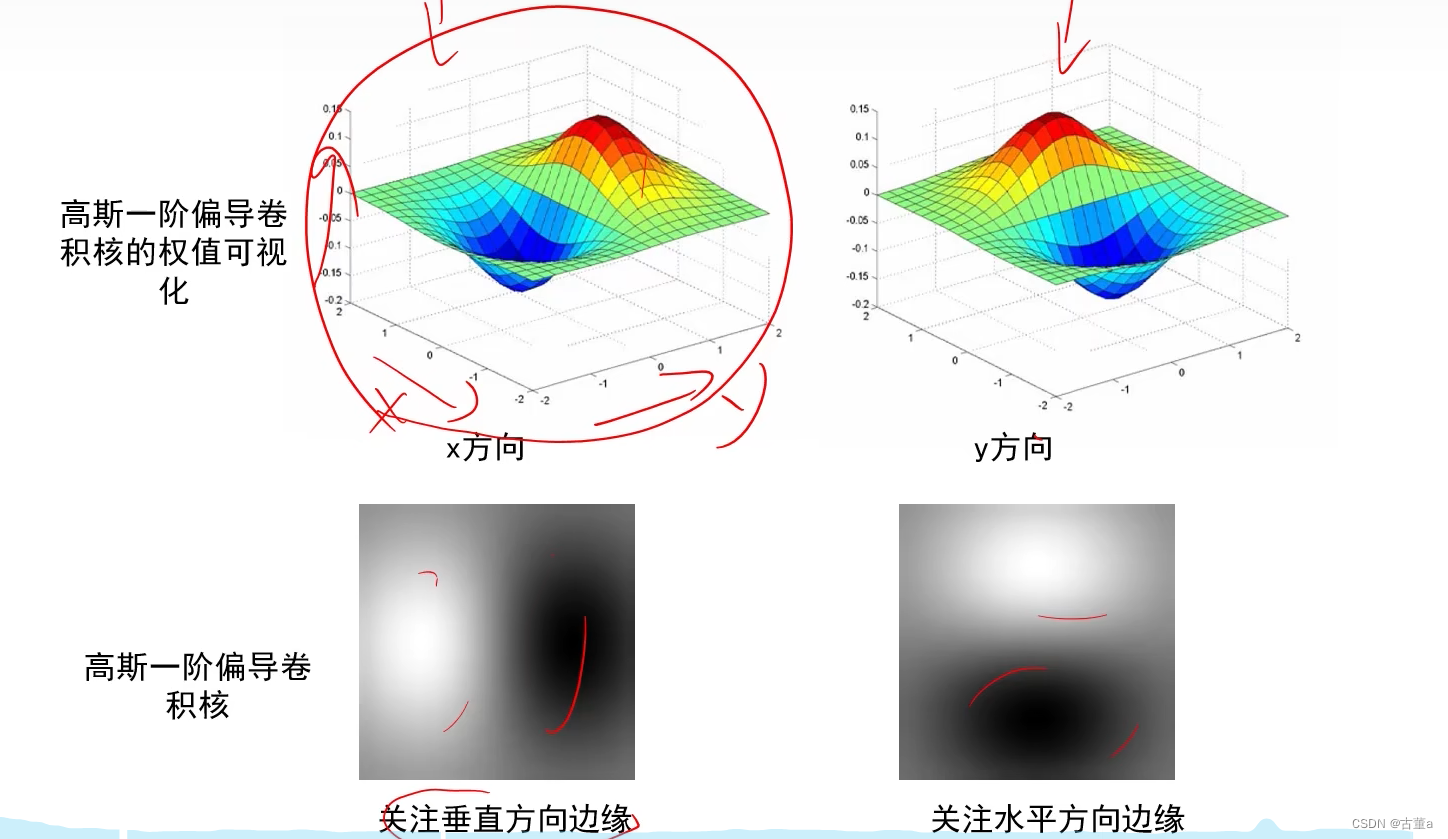
x方向求导,检测的是横向像素间差别,求出来是y方向的边。
y方向求导,检测的是纵向像素间差别,求出来是x方向的边。
图像梯度
Δ
f
=
[
∂
f
∂
x
,
∂
f
∂
y
]
Δf = [\frac{{\partial f}}{{\partial x}},\frac{{\partial f}}{{\partial y}}]
Δf=[∂x∂f,∂y∂f]
即两个方向的导数组成的向量
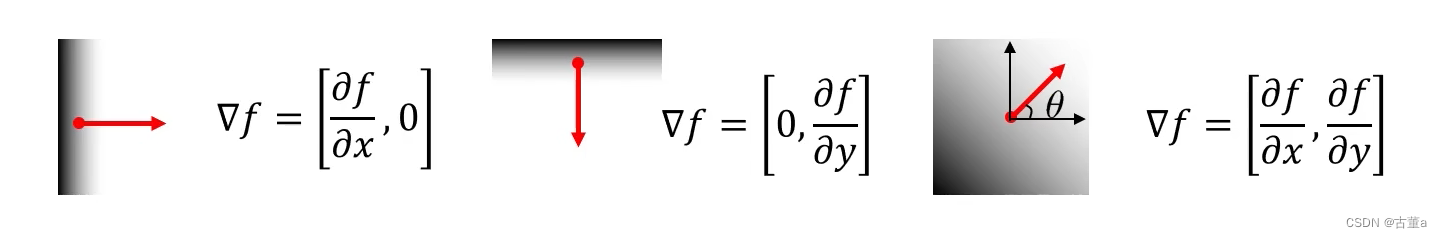
图像梯度的方向
与边缘方向垂直
梯度方向=arctan(对y偏导数 / 对x偏导数)
θ = arctan ( ∂ f ∂ x , ∂ f ∂ y ) \theta = \arctan\left(\frac{{\partial f}}{{\partial x}}, \frac{{\partial f}}{{\partial y}}\right) θ=arctan(∂x∂f,∂y∂f)
梯度方向与信号的方向垂直,求出梯度方向就可以知道信号的方向。
梯度方向是灰度变换最快的方向。
图像梯度的模
用 图像梯度的模 来反映图像的边缘信息。
∣
∣
V
f
∣
∣
=
(
∂
f
∂
x
)
2
+
(
∂
f
∂
y
)
2
|\left|{\mathcal{V}}f\right||={\sqrt{\left({\frac{\partial f}{\partial x}}\right)^{2}+\left({\frac{\partial f}{\partial y}}\right)^{2}}}
∣∣Vf∣∣=(∂x∂f)2+(∂y∂f)2
梯度模:值越大表示当前点是边缘的可能性越大。

噪声的影响
噪声图像的某一行或列的灰度值随位置变换的情况
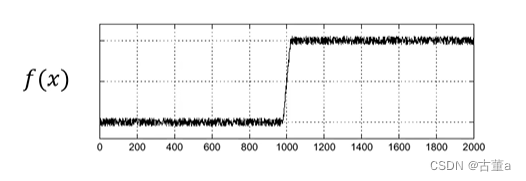
噪声影响带来的问题
若对灰度函数直接求导,图像中不能确定最大导数位置。
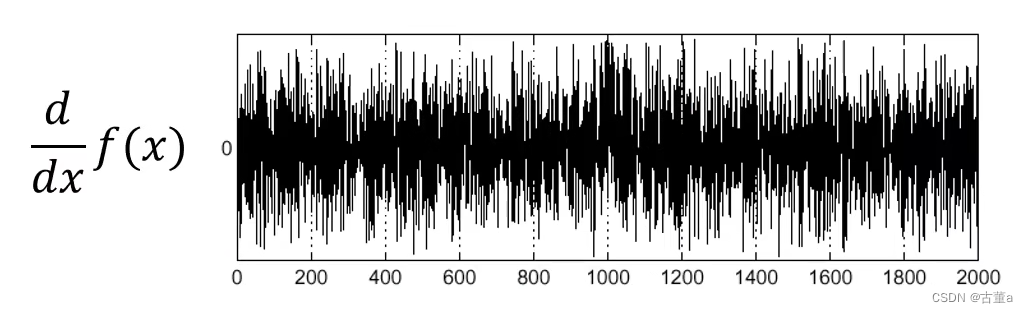
解决办法(先平滑处理)
高斯核去噪
从图像上看,每个点都有噪声,这是高斯噪声的特点,所以考虑使用高斯核去噪平滑,之后对去噪后的信号求导。
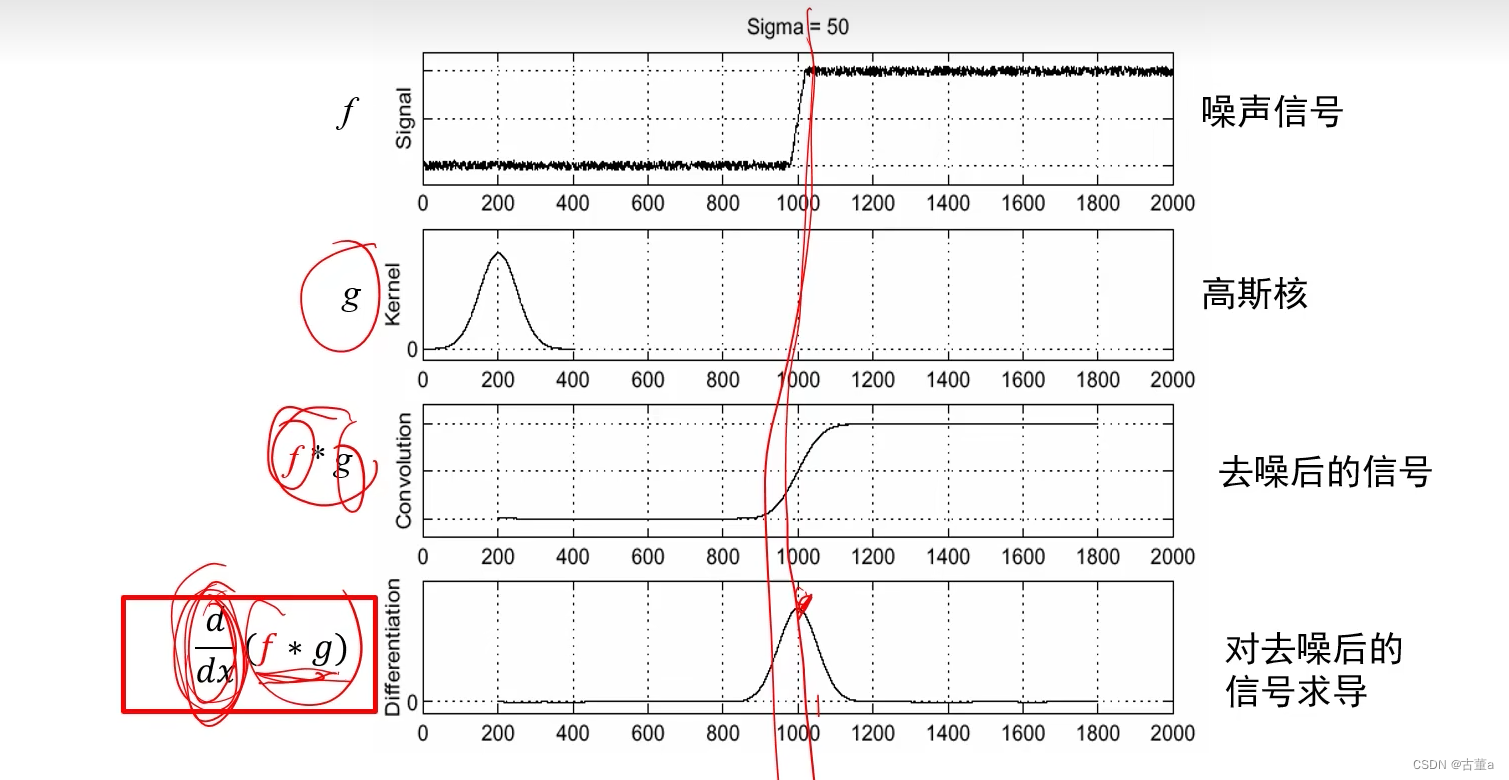
缺点:需要进行2次卷积操作,一次f *g,一次求x偏导
- 第一次卷积:高斯去噪
- 第二次卷积:图像求导(对x求偏导 − 1 ∣ 1 -1|1 −1∣1,对y求偏导 1 − 1 \frac{1}{-1} −11)
解决办法:卷积交换律(高斯一阶偏导核)
先对高斯卷积核(平滑)进行求导卷积(求导),得到新的卷积核(求导+平滑),再
用这个新的卷积核与原图卷积。
高斯一阶偏导核
高斯卷积+求导卷积
d d x ( f ∗ g ) = f ∗ d d x g \frac{d}{d x}(f*g)=f*\frac{d}{d x}\,g dxd(f∗g)=f∗dxdg
微分是卷积,而卷积具有结合性
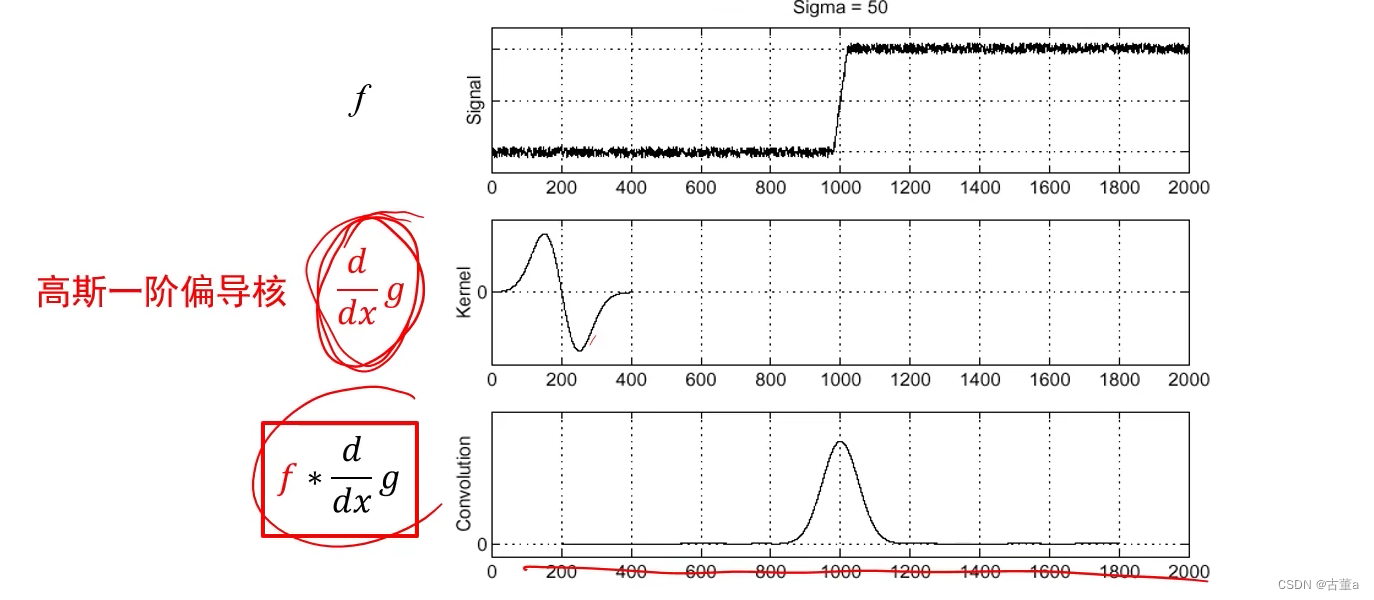
节约了一次图像卷积的操作!
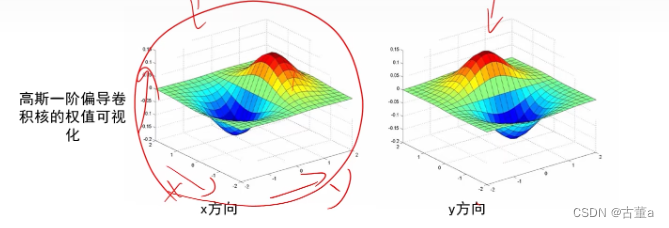
高斯一阶偏导核权值可视化
一半正,一半负。
高斯一阶偏导卷积核的方差参数

上图中,从左到右,高斯一阶偏导卷积核的方差分别为1,3,7。
- 方差大,提取粗粒度轮廓。
- 方差小,提取细粒度轮廓。
高斯核 vs 高斯一阶偏导核
高斯核
- 消除高频成分(低通滤波器)
- 卷积核中的权值不可为负数
- 权值总和为1(恒定区域不受卷积影响)

高斯一阶偏导核
-
高斯的导数
-
卷积核中的权值可以为负
-
权值总和是0(恒定区域无响应)
- 恒定区域无响应,即恒定区域不会有边缘
- 例如一张全白的图,使用[-3,2] 求导, 1 ∗ ( − 3 ) + 1 ∗ 2 = − 1 1 * (-3) + 1 * 2 = -1 1∗(−3)+1∗2=−1,计算结果显示有梯度,与实际不符,全白的图不可能有梯度。所以必须使得权值总和为0,保证像这样的情况才不会出错。
-
高对比度点的响应值大
- 响应值越大,表示该点是边缘点的概率越大。

- 响应值越大,表示该点是边缘点的概率越大。
边缘检测目标
Canny边缘检测器

高斯一阶偏导核卷积图像

期望得到上图中右图所示很精确的边缘。
高斯一阶偏导核卷积图像的缺点
计算每个点的梯度幅值和方向。
- 梯度幅值:用来描述该点是不是边缘。
- 期望得到上图中右图所示很精确的边缘。
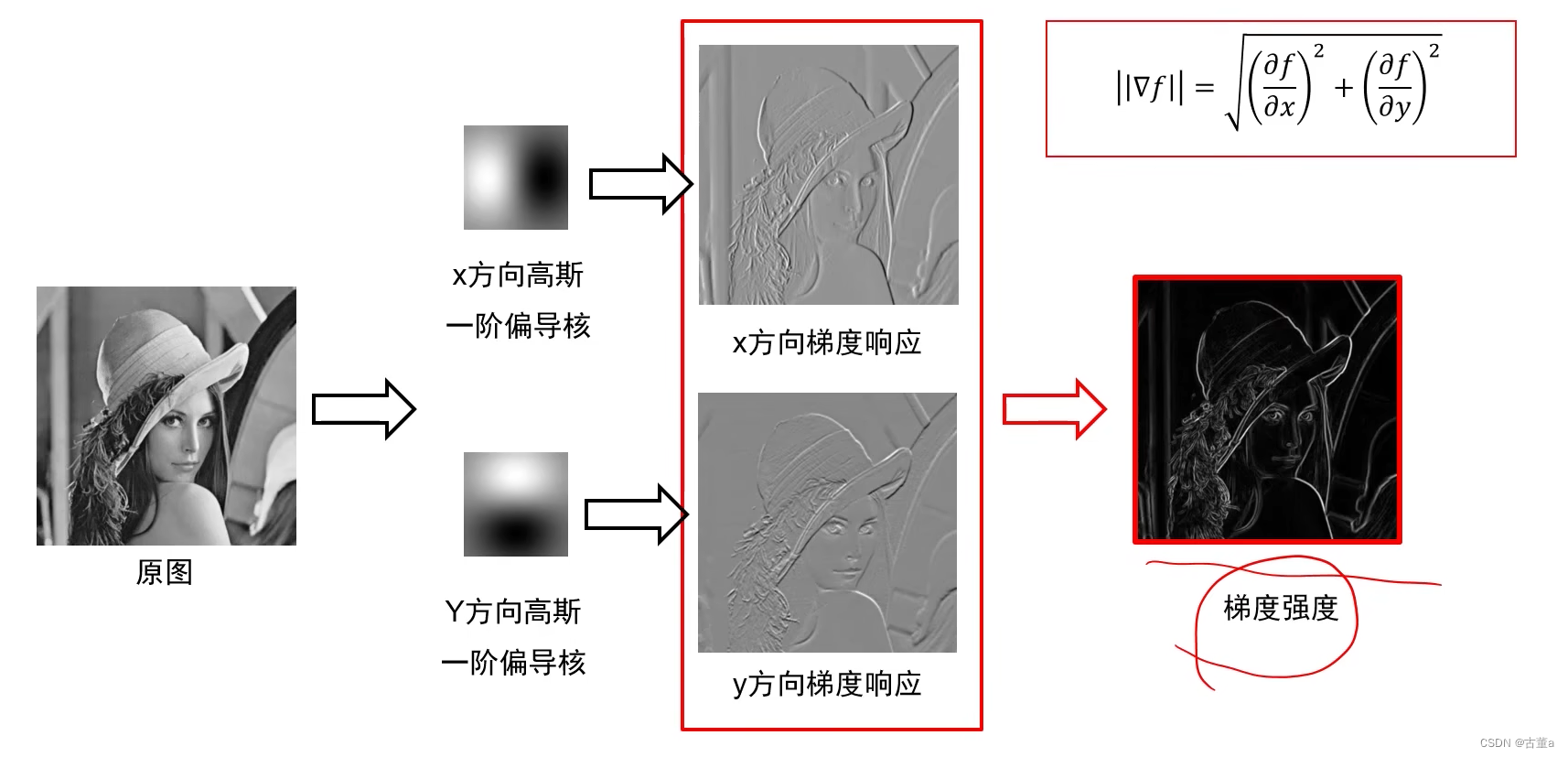
经过高斯一阶偏导核的处理,梯度强度边缘很粗,因为边缘附近的信号,从左到右是慢慢改变的,而不是突然改变的阶梯型,但边缘检测想要更细的边,就需要非极大值抑制。

非极大值抑制
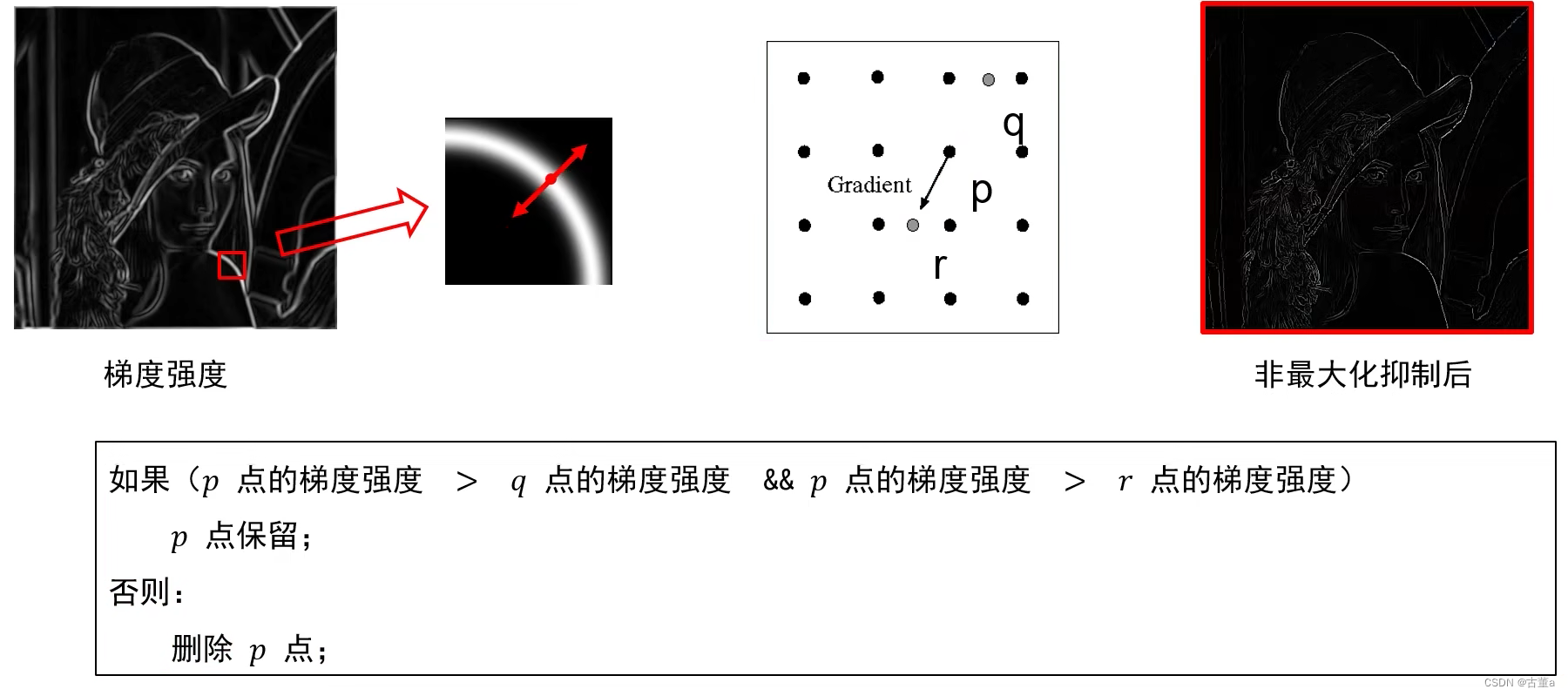
p跟梯度方向的正方向距离为1的 r 和反方向距离为1的 q 比较梯度强度。
梯度强度p > q && p > r,则保留p点,否则删除p点。
提示:q 点、r 点坐标通常不是整数,其对应的强度需要插值获得!!!
一般r和q不在图像正规的像素点上,通常r和q点的强度需要周边的点加权求和来获得。
但,非最大化抑制的结果中有噪声,需要通过门限值对噪声进行过滤。
门限过滤

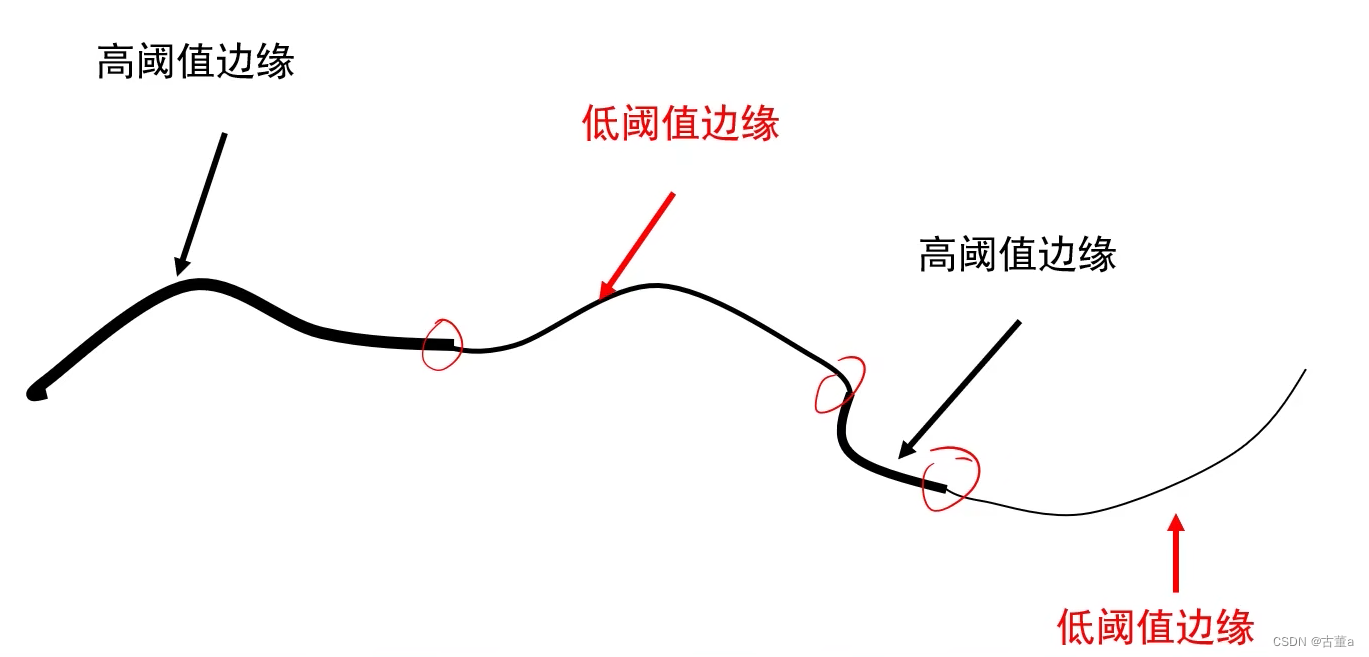
Canny如何选择去噪时的门限值?- 双阈值
- 高阈值门限:提取高骨干边缘曲线。
- 低阈值门限:提取链接骨干的边缘曲线。低阈值会筛选出很多边,但只保留与高阈值提取的边有关系的边。