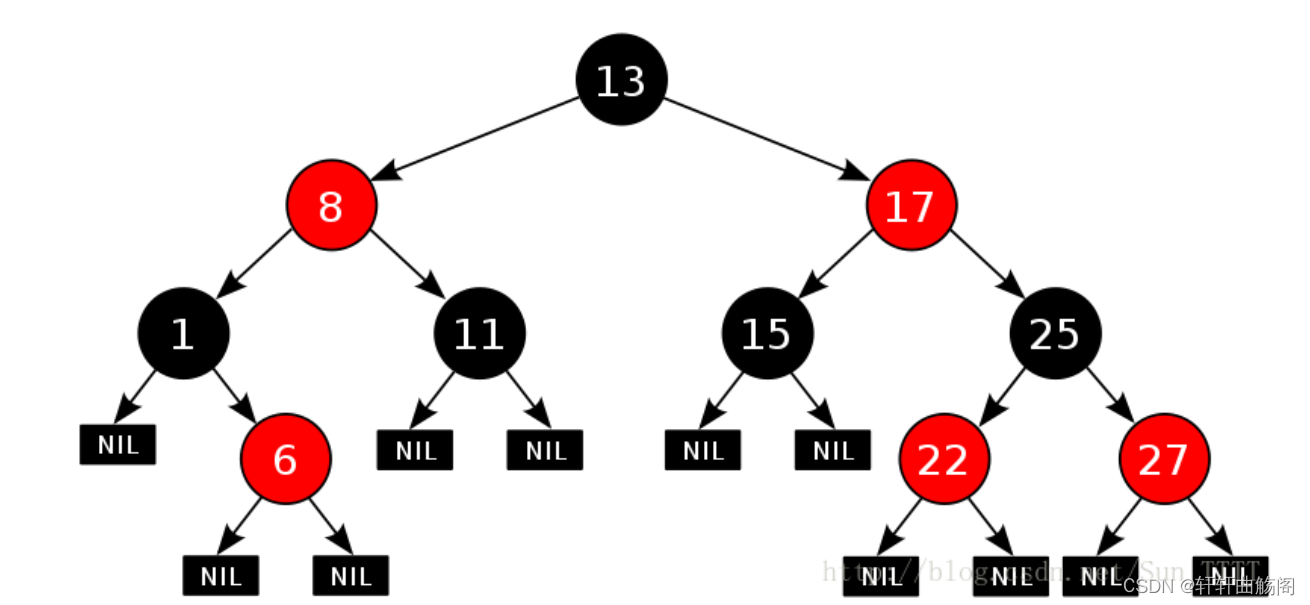
1.什么是红黑树?
红黑树是一种特定类型的二叉树,用于组织数据。它是一种平衡二叉查找树(AVL树)的变体,每个结点都带有颜色属性(红色或黑色)。在红黑树中,从根到叶子的最长的可能路径不多于最短的可能路径的两倍长。具体来说,红黑树满足以下性质:
- 每个结点要么是红色,要么是黑色。
- 根结点是黑色。
- 每个叶结点(NIL或空结点)是黑色的。
- 如果一个结点是红色的,则它的两个子结点都是黑色的。
- 对于每个结点,从该结点到其所有后代叶结点的简单路径上,均包含相同数目的黑色结点。
举个例子
2.红黑树插入的模拟实现
①节点的定义
// 在这里为了方便表示我们先将颜色枚举
// 在红黑树中只有黑与红,即BLACK与RED
enum Color
{
BLACK,
RED
};
// 因为节点是公用的,因此设定为struct
template<class K, class V>
struct RBTreeNode
{
RBTreeNode(const pair<K, V>& kv)
:_kv(kv)
, _left(nullptr)
, _right(nullptr)
, _parent(nullptr)
// 根据红黑树的性质可以知道
// 要插入的新节点不应该是黑色的,而应该是红色的
// 如果是黑色的那么就会影响它当前路径的黑色节点总数
, _color(RED)
{}
pair<K, V> _kv;
RBTreeNode<K, V>* _left;
RBTreeNode<K, V>* _right;
RBTreeNode<K, V>* _parent;
Color _color;
};②插入
template<class K, class V>
class RBTree
{
typedef RBTreeNode<K, V> Node;
bool Insert(const pair<K, V>& kv)
{
if (_root == nullptr)
{
_root = new Node(kv);
return true;
}
Node* cur = _root;
Node* parent = nullptr;
// 寻找要插入的位置
while (cur)
{
if (kv.first < cur->_kv.first)
{
parent = cur;
cur = cur->_left;
}
else if (kv.first > cur->_kv.first)
{
parent = cur;
cur = cur->_right;
}
else
{
return false;
}
}
// 到此处cur已经指向了应该插入的位置,
// 然后判断应该插入到parent的哪边
cur = new Node(kv);
if (kv.first > parent->_kv.first)
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
cur->_parent = parent;
// 插入完成后需要对红黑树进行调整
// 若父节点是黑就无需调整
// 而当父节点是红就需要进行调整
// ...
}
private:
Node* _root = nullptr;
};
以上面的红黑树为例,在parent为红的情况下,插入之后的情况可以将它们大致分为两种:1. uncle存在且为红;2.uncle不存在或uncle存在且为黑。让我们来分析一下,在这里我们依旧采取先具体后推广到一般的方法
1.uncle存在且为红
先举一个具体例子
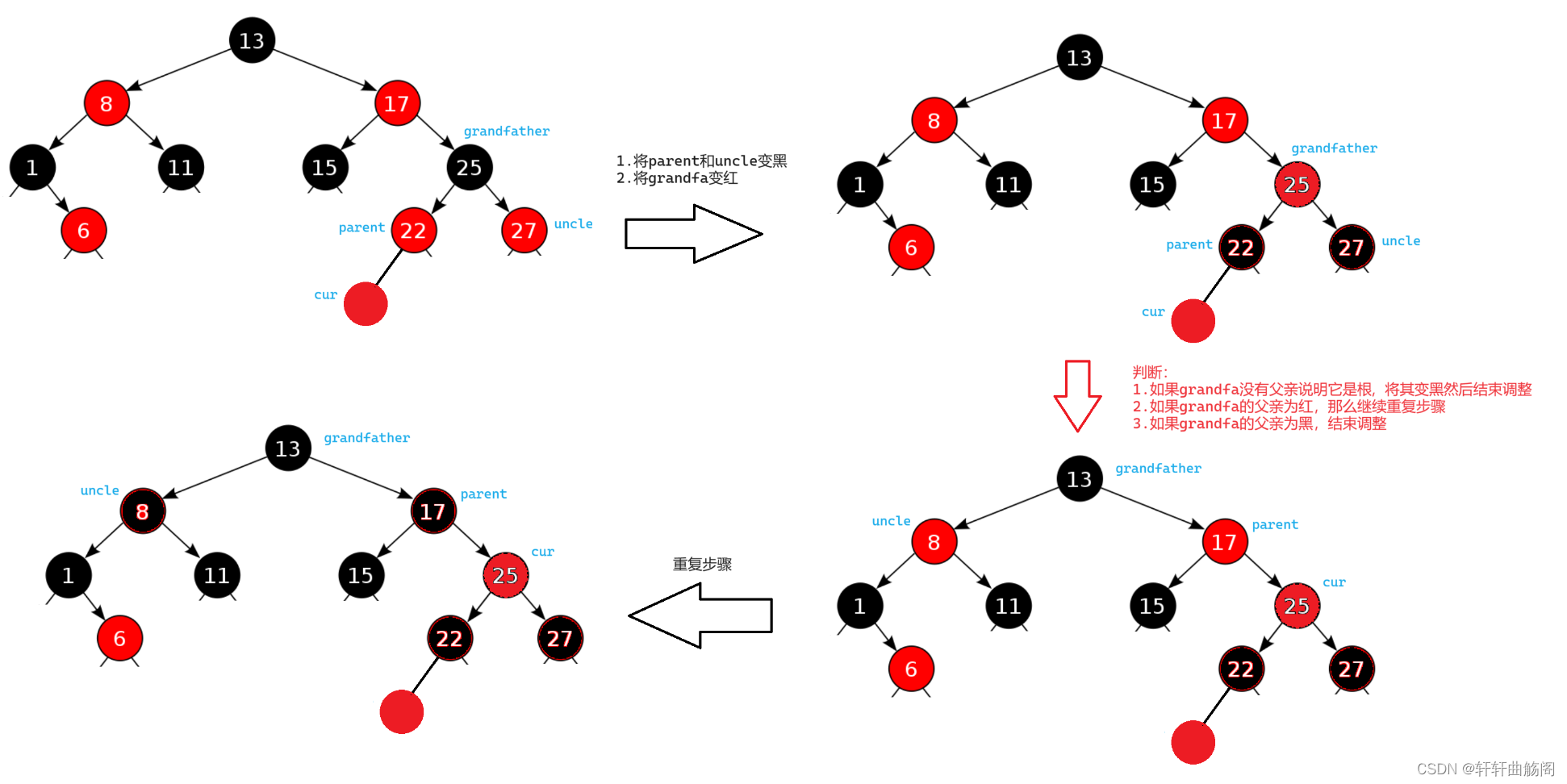
抽象图如下

2.uncle不存在或uncle存在且为黑
先举一个uncle不存在的具体例子

再举一个uncle存在且为黑的具体例子
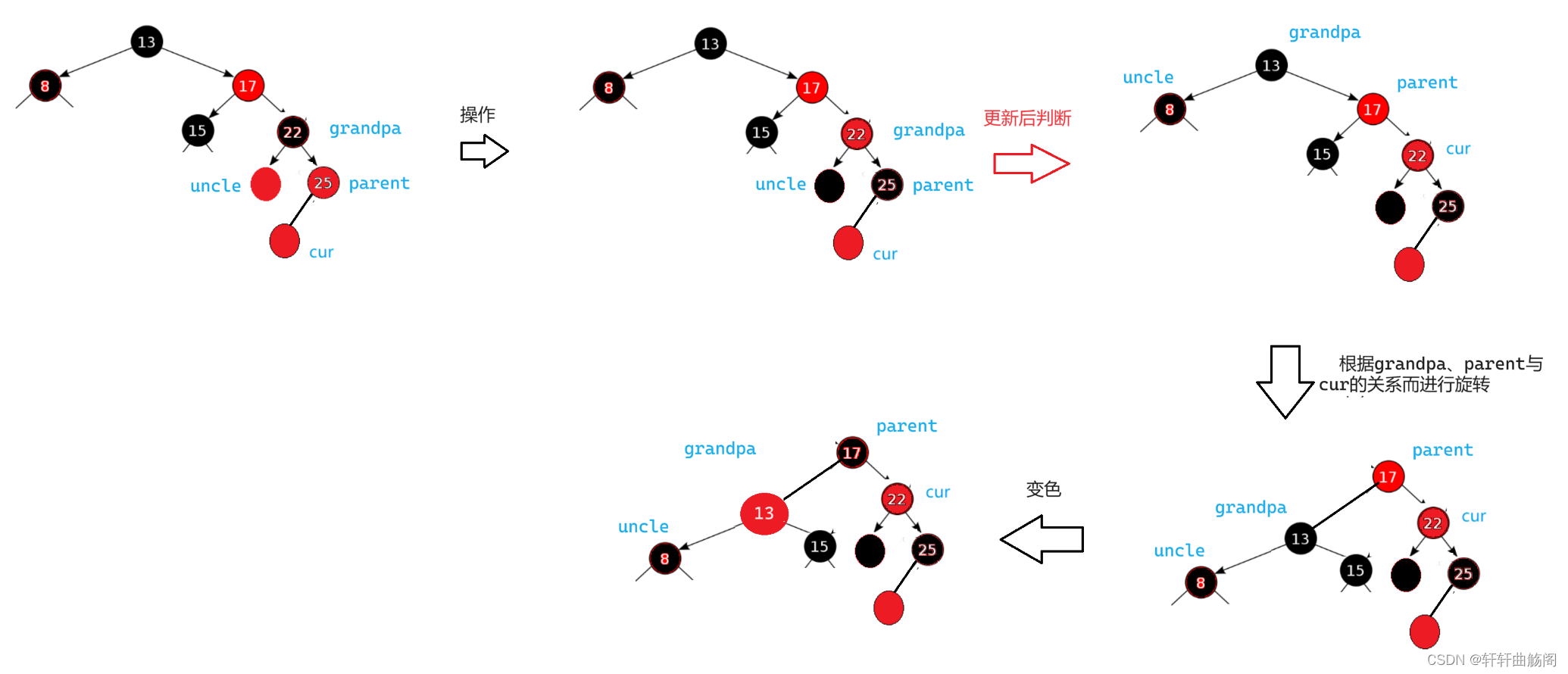
观察上述例子之后可以发现,这两种情况本质上可以当做同一操作,那就是先判断grandpa、parent与cur的关系,然后根据具体情况进行旋转,旋转之后进行变色,因此抽象图如下


综合上面的所有情况,再加上一些细节我们可以得到如下插入代码
bool Insert(const pair<K, V>& kv)
{
if (_root == nullptr)
{
_root = new Node(kv);
return true;
}
Node* cur = _root;
Node* parent = nullptr;
// 寻找要插入的位置
while (cur)
{
if (kv.first < cur->_kv.first)
{
parent = cur;
cur = cur->_left;
}
else if (kv.first > cur->_kv.first)
{
parent = cur;
cur = cur->_right;
}
else
{
return false;
}
}
// 到此处cur已经指向了应该插入的位置,
// 然后判断应该插入到parent的哪边
cur = new Node(kv);
if (kv.first > parent->_kv.first)
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
cur->_parent = parent;
// 插入完成后判断一下
// 若父节点是黑就无需调整
// 而当父节点是红就需要进行调整
while (parent && parent->_color == RED)
{
Node* grandpa = parent->_parent;
if (parent == grandpa->_left)
{
Node* uncle = parent->_right;
if (uncle && uncle->_color == RED)
{
uncle->_color = parent->_color = BLACK;
grandpa->_color = RED;
cur = grandpa;
parent = cur->_parent;
}
else
{
if (uncle == nullptr)
{
if (parent->_left == cur)
{
// grandpa
// parent
//cur
RotateR(grandpa);
grandpa->_color = RED;
parent->_color = BLACK;
}
else
{
// grandpa
// parent
// cur
RotateL(parent);
RotateR(grandpa);
cur->_color = BLACK;
grandpa->_color = RED;
}
}
else // uncle存在且为黑
{
if (parent->_left == cur)
{
// grandpa
// parent
//cur
RotateR(grandpa);
grandpa->_color = RED;
parent->_color = BLACK;
}
else
{
// grandpa
// parent
// cur
RotateL(parent);
RotateR(grandpa);
cur->_color = BLACK;
grandpa->_color = RED;
}
}
break;
}
}
else // parent == grandpa->_right
{
Node* uncle = parent->_left;
if (uncle && uncle->_color == RED)
{
uncle->_color = parent->_color = BLACK;
grandpa->_color = RED;
cur = grandpa;
parent = cur->_parent;
}
else
{
if (uncle == nullptr)
{
if (parent->_left == cur)
{
//grandpa
// parent
//cur
RotateR(parent);
RotateL(grandpa);
cur->_color = BLACK;
grandpa->_color = RED;
}
else
{
//grandpa
// parent
// cur
RotateL(grandpa);
grandpa->_color = RED;
parent->_color = BLACK;
}
}
else // uncle存在且为黑
{
if (parent->_left == cur)
{
//grandpa
// parent
//cur
RotateR(parent);
RotateL(grandpa);
cur->_color = BLACK;
grandpa->_color = RED;
}
else
{
//grandpa
// parent
// cur
RotateL(grandpa);
grandpa->_color = RED;
parent->_color = BLACK;
}
}
break;
}
}
}
return true;
}(注:左右旋参见数据结构——AVL树)
3.红黑树的性能分析
红黑树可以在O(log n)时间内做查找、插入和删除,这里的n 是树中元素的数目。红黑树在最坏情况下的运行时间也是非常良好的,并且在实践中是高效的。红黑树的性能受限于它的平衡性,即每个叶子节点到根节点的路径上所包含的黑色节点的数量是相同的,这也被称为黑色完美平衡。保持这种平衡可以确保红黑树的性能稳定。总的来说,红黑树是一种高效的数据结构,适用于许多不同的情况。
4.红黑树与AVL树的比较
红黑树和AVL树都是高效的平衡二叉树,增删改查的时间复杂度都是O($log_2 N$),红黑树不追求绝对平衡,其只需保证最长路径不超过最短路径的2倍,相对而言,降低了插入和旋转的次数,所以在经常进行增删的结构中性能比AVL树更优,而且红黑树实现比较简单,所以实际运用中红黑树更多。






