1.典型例题
28. 找出字符串中第一个匹配项的下标 - 力扣(LeetCode)
题干:给你两个字符串
haystack和needle,请你在haystack字符串中找出needle字符串的第一个匹配项的下标(下标从 0 开始)。如果needle不是haystack的一部分,则返回-1。示例 1:
输入:haystack = "sadbutsad", needle = "sad" 输出:0 解释:"sad" 在下标 0 和 6 处匹配。 第一个匹配项的下标是 0 ,所以返回 0 。示例 2:
输入:haystack = "leetcode", needle = "leeto" 输出:-1 解释:"leeto" 没有在 "leetcode" 中出现,所以返回 -1 。提示:
1 <= haystack.length, needle.length <= 104haystack和needle仅由小写英文字符组成
1.1暴力求解
昨天我们也时间c语言中关于strstr()函数的模拟实现,用暴力求解当然不在话下.
以下附上暴力求解的代码(c语言)
int strStr(char * haystack, char * needle){
if(*needle == '\0')
{
return 0;
}
char* cp;
char* s1;
char* s2;
int count = 0;
cp = haystack;
while(*cp)
{
s1 = cp;
s2 = needle;
while(*s1 &&*s2 &&*s1 == *s2)
{
s1++;
s2++;
}
if(*s2 == '\0')
{
return count;
}
count++;
cp++;
}
return -1;
}2.KMP算法解决这类查找子串的问题
我将从如下顺序来依次讲解KMP算法的操作以及实现过程(最后会附上代码实现)
1.什么是KMP算法
2.KMP算法有啥用
3.前缀表的定义
4.为什么是前缀表
5.如何计算前缀表
6.前缀表和Next数组之间的关系
7.使用Next数组来匹配
8.时间复杂度的分析
9.构造Next数组
10.使用Next数组来匹配
11.代码实现
2.1 什么是KMP算法
我们先介绍一下KMP算法的由来吧,它是由Knuth,Morris和Pratt三位学者发明的,所以选取了三位学者的首字母命名.
2.2 KMP算法有啥用
KMP算法主要用于字符串匹配问题的解决.
主要思想: 当出现字符串不匹配时,可以知道一部分之前已经匹配的字符串内容,从而不需要从头开始重新匹配,减少了时间复杂度.
KMP算法的核心就是这个Next数组了,它也就是保证不从头开始匹配的关键,
这里我们要把Next数组的运行机制搞明白,也要把它的原理搞明白,下面我们就开始看Next数组.
2.3 前缀表的定义
实际上所谓的Next数组,也就是一个前缀表(Prefix),那么前缀表有啥用呢?
前缀表用于回退,当主串和子串开始不匹配时,前缀表就记录了子串应该从哪里开始重新匹配
举例:在主串: aabaabaafa 中查找子串 aabaaf
我们发现子串在第6个字符f发生了不匹配,如果是暴力求解的方式,这里我们就要从头开始匹配了,但是使用前缀表我们就会从子串第三个字符开始匹配.
那么前缀表是如何记录的呢?
首先我们要知道前缀表的任务是当前位置匹配失败,找到之前已经匹配上的位置,再重新匹配,这样意味着在某个字符失配时,前缀表会告诉你在下一步匹配中,子串该跳到哪个位置.
前缀表:记录下标i之前(包含i)的字符串中,有多大长度的相同前后缀.
前缀:不包含最后一个字符的所有以第一个字符为开头的连续子串,例如上文子串中的a,aab..
后缀:同上,不包含首字母,例如fa,aafa...
2.4 为什么是前缀表
刚刚我们子串的跳转过程是
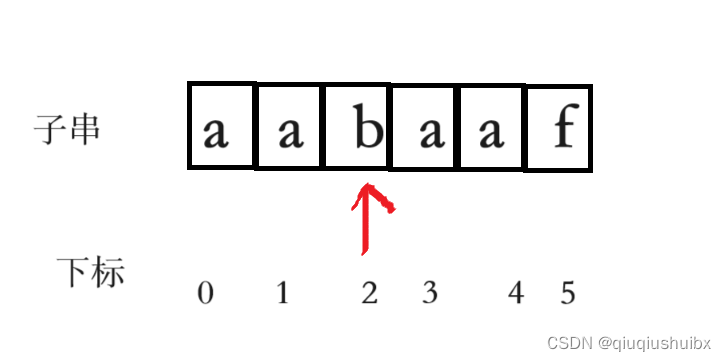
下标5之前这部分的字符串(也就是字符串aabaa)的最长相等的前缀 和 后缀字符串是 子字符串aa ,因为找到了最长相等的前缀和后缀,匹配失败的位置是后缀子串的后面,那么我们找到与其相同的前缀的后面从新匹配就可以了。
2.5 如何计算前缀表
我们以aabaaf举例
前缀表的元素就是其子串的最长相等前后缀的元素
a 0
aa 1
aab 0
aaba 1
aabaa 2
aabaaf 0
我们这时候找到不匹配的字符f,找到它前一个字符所对应的前缀表的数值,数值是2,所以直接跳转到下标为2的字符b开始重新匹配,最后就找到了和主串匹配的子串了.
2.6 前缀表和Next数组之间的关系
关于网上对Next数组的定义,有的直接用前缀表,有的用前缀表右移一位,第一个元素赋值为-1,有的则使用前缀表所有的元素-1,最后再加回来,这里方式多样,不做过多赘述,这里不涉及KMP算法的核心,有多种实现方式都可行.
2.7 时间复杂度的分析
这里假设m是主串长度,n是子串长度,由于在匹配中,前缀表不断的调整位置,匹配的过程是O(n),但是还要单独实现Next数组,复杂度是O(m),所以整个KMP算法的时间复杂度是O(m+n)
暴力求解遍历两个字符串显而易见是O(m*n),所以KMP算法在字符串匹配的过程中极大的提高了搜索的效率.
2.8 构造Next数组
我们定义一个函数getNext来构建next数组,函数参数为指向next数组的指针,和一个字符串。代码如下:
void getNext(int* next, const string& s)构造Next数组其实本质上就是计算子串的前缀表的过程,我们分为以下三步 :
1.初始化
2.处理前后缀相同情况
3.处理前后缀不相同情况
2.8.1 初始化
定义两个指针i,j, j用来指向前缀起始位置,i用来指向后缀起始位置
下面对next数组赋初值
int j = -1; next[0] = j;j还有一个含义就是最长相等前后缀的大小,所以next[0] = j
2.8.2 处理前后缀不等情况
因为j初始化为-1,所以i就从1开始,进行s[i] 和 s[j+1]比较
for(int i = 1; i < s.size(); i++) {
如果他们不相等就要进行回退操作
while (j >= 0 && s[i] != s[j + 1]) { // 前后缀不相同了 j = next[j]; // 向前回退 }
2.8.2 处理前后缀相等情况
if (s[i] == s[j + 1]) { // 找到相同的前后缀
j++;
}
next[i] = j;
getNext最终代码
void getNext(int* next, const string& s){
int j = -1;
next[0] = j;
for(int i = 1; i < s.size(); i++) { // 注意i从1开始
while (j >= 0 && s[i] != s[j + 1]) { // 前后缀不相同了
j = next[j]; // 向前回退
}
if (s[i] == s[j + 1]) { // 找到相同的前后缀
j++;
}
next[i] = j; // 将j(前缀的长度)赋给next[i]
}
}2.9 使用Next数组来匹配
在主串s里 找是否出现过子串t。
定义两个下标j指向子串起始位置,i指向主串起始位置
j依然为-1,因为next数组的起始位置为-1
这时候i从0开始遍历主串
for (int i = 0; i < s.size(); i++)如果s[i] 与 t[j + 1] 不相同,就要到next数组中寻找下一个匹配的位置
while(j >= 0 && s[i] != t[j + 1]) { j = next[j]; }相同的话i和j同时向后移动
if (s[i] == t[j + 1]) { j++; // i的增加在for循环里 }那么如何判断主串完全包含子串呢?
当j指向子串的最后一个字母时,就说明完全包含
if (j == (t.size() - 1) ) { return (i - t.size() + 1); }
int j = -1; // 因为next数组里记录的起始位置为-1
for (int i = 0; i < s.size(); i++) { // 注意i就从0开始
while(j >= 0 && s[i] != t[j + 1]) { // 不匹配
j = next[j]; // j 寻找之前匹配的位置
}
if (s[i] == t[j + 1]) { // 匹配,j和i同时向后移动
j++; // i的增加在for循环里
}
if (j == (t.size() - 1) ) { // 文本串s里出现了模式串t
return (i - t.size() + 1);
}
}2.10 代码实现
class Solution {
public:
void getNext(int* next, const string& s) {
int j = -1;
next[0] = j;
for(int i = 1; i < s.size(); i++) { // 注意i从1开始
while (j >= 0 && s[i] != s[j + 1]) { // 前后缀不相同了
j = next[j]; // 向前回退
}
if (s[i] == s[j + 1]) { // 找到相同的前后缀
j++;
}
next[i] = j; // 将j(前缀的长度)赋给next[i]
}
}
int strStr(string haystack, string needle) {
if (needle.size() == 0) {
return 0;
}
int next[needle.size()];
getNext(next, needle);
int j = -1; // // 因为next数组里记录的起始位置为-1
for (int i = 0; i < haystack.size(); i++) { // 注意i就从0开始
while(j >= 0 && haystack[i] != needle[j + 1]) { // 不匹配
j = next[j]; // j 寻找之前匹配的位置
}
if (haystack[i] == needle[j + 1]) { // 匹配,j和i同时向后移动
j++; // i的增加在for循环里
}
if (j == (needle.size() - 1) ) { // 文本串s里出现了模式串t
return (i - needle.size() + 1);
}
}
return -1;
}
};java版本
class Solution {
public void getNext(int[] next, String s){
int j = -1;
next[0] = j;
for (int i = 1; i<s.length(); i++){
while(j>=0 && s.charAt(i) != s.charAt(j+1)){
j=next[j];
}
if(s.charAt(i)==s.charAt(j+1)){
j++;
}
next[i] = j;
}
}
public int strStr(String haystack, String needle) {
if(needle.length()==0){
return 0;
}
int[] next = new int[needle.length()];
getNext(next, needle);
int j = -1;
for(int i = 0; i<haystack.length();i++){
while(j>=0 && haystack.charAt(i) != needle.charAt(j+1)){
j = next[j];
}
if(haystack.charAt(i)==needle.charAt(j+1)){
j++;
}
if(j==needle.length()-1){
return (i-needle.length()+1);
}
}
return -1;
}
}注:参考代码随想录的解法,附上B站视频







