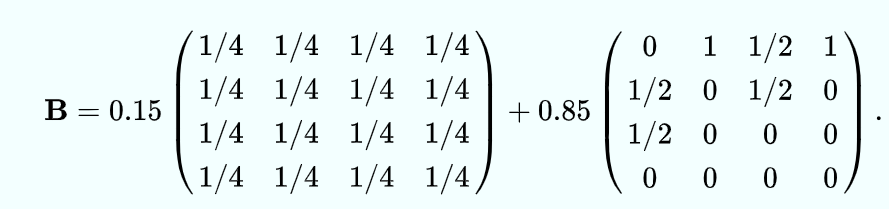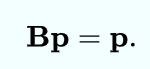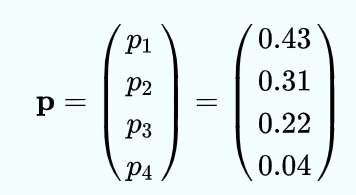地址:http://immersivemath.com/ila/index.html
这是全球第一本带交互式图形的线性代数教材,作者是 J. Ström, K. Åström, and T. Akenine-Möller。
全书一共十章,各章节内容如下:

接下来我将对各章节进行简单的总结,另外请注意,阅读过程中请一定不要忘记各章节提供的的可交互图表。
第一章:简介
第一章主要交代了两件事情,第一个是关于符号说明,这个几乎在所有书籍中都有,主要就是告诉你用什么符号表示向量,用什么符号表示矩阵等等。
第二个事情就是回顾了一下三角函数的知识,不要惊讶为什么几何学的东西会出现在这里,三角函数在很多领域都有所应用,在机器学习领域,可以用来计算向量的余弦相似性,而余弦相似性又可以作为目标函数的一种评价指标。
第二章:向量
向量可以说是线性代数中最基础的东西了,就连线性代数的另一大主角矩阵也可以看作是向量的排列组合。
直白地讲,向量就是一组数字的集合,向量存在的最大意义是它们提供了一种有效的数学工具,用于描述和处理现实世界中的各种实体,并在向量空间中发掘实体间的各种关系。
第三章:向量的点积
这是继向量加法,向量与标量乘法后,另一个重要的向量操作,向量的点积是两个向量之间的乘法运算,结果是它们对应分量的乘积之和。其作用是计算向量之间的夹角、判断正交性、进行投影和分解、计算相似性和相关性等。
向量的点积是非常重要且经常使用的概念,例如,计算机图形学中光线追踪算法。
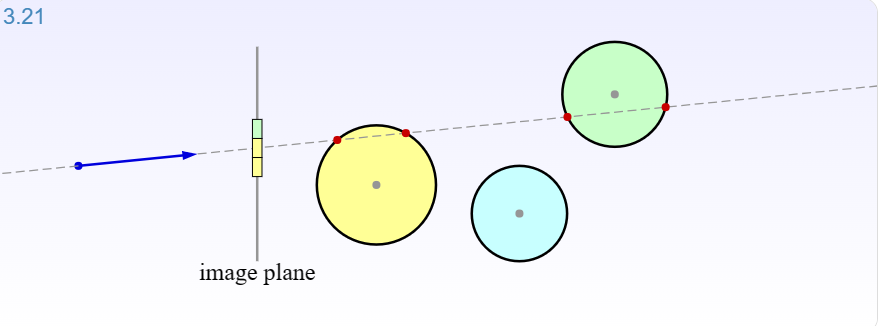
第四章:向量的叉积
这是继向量加法,向量与标量乘法,向量点积后,最后一个重要的向量操作,与点积结果为标量不同,叉积的结果仍然是一个向量,也就是说比点点积多了一个方向信息。
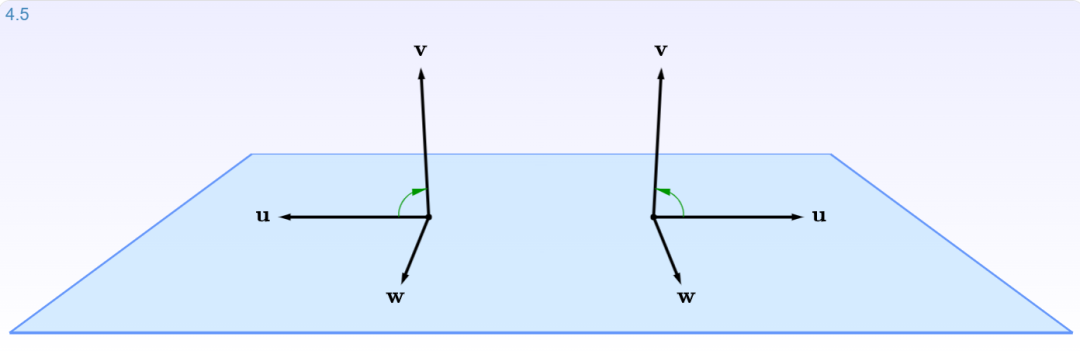
举个应用的例子,计算四面体的体积。
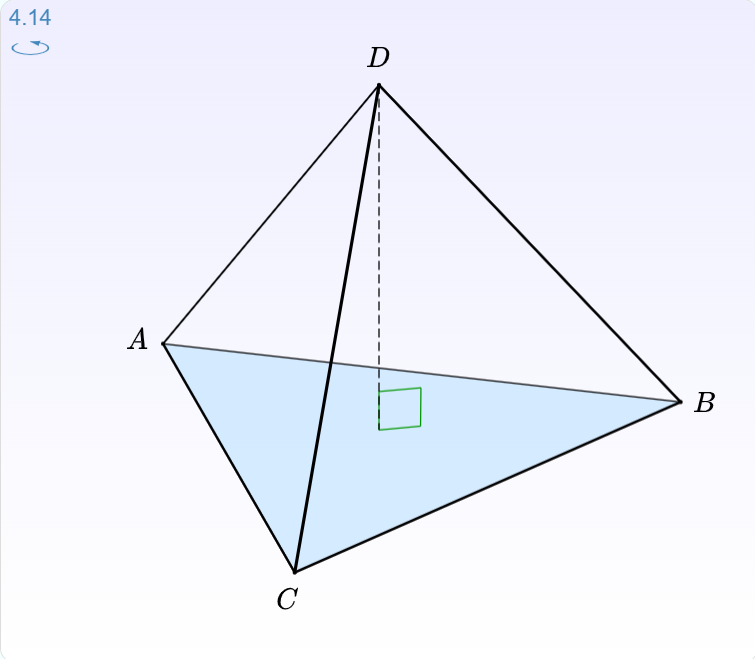
用四个点表示成三个向量。
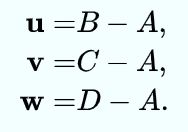
则四面体的体积为:
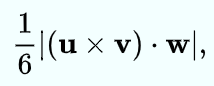
第五章:高斯消元
高斯消元是一种求解线性方程组的方法,也可以用于求矩阵的逆,其实我们在小学就接触过高斯消元,只不过小学学的都是有唯一解的二元一次方程组。
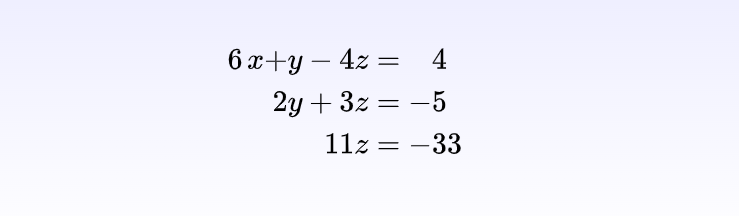
本章节提供了一个实际应用的例子:视频压缩,大家可以研究一下。

第六章:矩阵
矩阵是线性代数中,除向量外的另一大主角,可以从两方面看待矩阵,一方面是静止的,例如,一幅图像可以用矩阵表示,另一方面是动态的,例如可以用矩阵表示一个变换。
对于矩阵,可以去探索一些属性,例如,对于图像进行主成分分析,就能实现降维的目的。计算矩阵的逆,就能快速求解线性方程组。分解矩阵,就能将复杂的问题简化。

第七章:矩阵的行列式
矩阵的行列式是一个方阵所对应的一个标量值。行列式可以看作是矩阵的一个重要属性,根据行列式的值可以进一步判断矩阵是否可逆,线性方程组的解的情况,计算特征值和特征向量等等。
第八章:矩阵的秩
矩阵的秩也可以看作是矩阵的一个非常重要的性质,矩阵的秩是指矩阵中线性独立的行或列的最大数量,也可以理解为矩阵中非零行(或列)的个数。
通过矩阵的秩可以判断矩阵行向量或者列向量的相关性,方程组解的存在性,矩阵的可逆性,以及特征值和特征向量的计算等,
本章提供了一个通过声音恢复结构的例子。

第九章:线性映射
线性映射是指在向量空间之间进行的一种特殊的映射关系,它保持向量的线性组合性质。简而言之,线性映射是指满足加法和数乘运算规则的映射。
具体来说,设有两个向量空间 V 和 W,一个映射 T: V → W 被称为线性映射,如果对于任意向量 u、v ∈ V 和标量 c,满足以下两个条件:
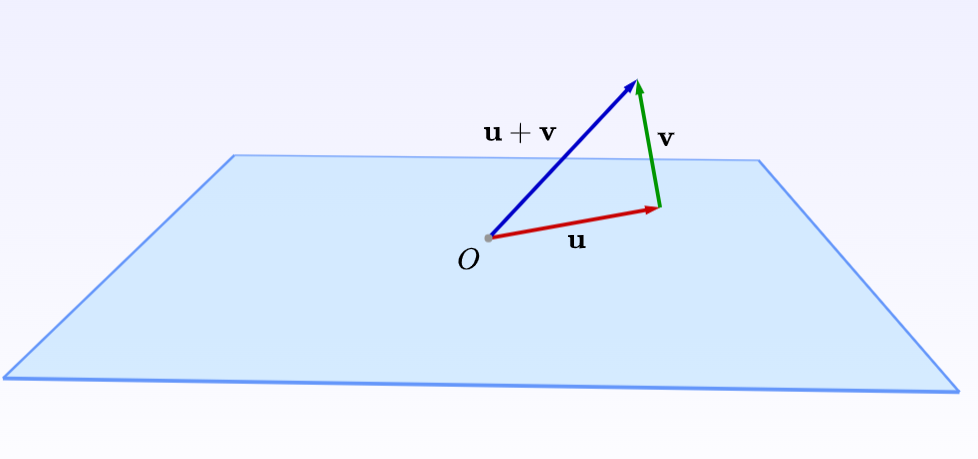
加法性:T(u + v) = T(u) + T(v)。即线性映射对向量的加法保持性质,映射后的结果等于分别映射后的结果相加。
数乘性:T(cu) = cT(u)。即线性映射对向量的数乘保持性质,映射后的结果等于数乘后再进行映射。
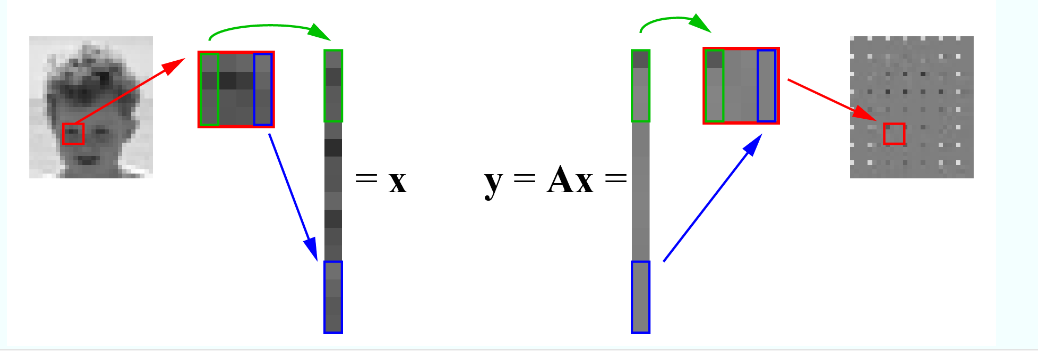
线性系统的性质就决定了其不能表示复杂映射能力,如果要想表示复杂映射关系,就要考虑非线性映射。这也是为什么要在神经网络中加入激活函数的原因。
第十章:特征值与特征向量
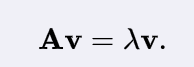
它是矩阵最重要的属性,没有之一。本章提供的例子也很经典。
特征脸

PageRank中稳态向量的求解