1.求解n阶导数
%%
%如何求解n阶导数,用到diff(f,n)
syms x;
f=sin(x)/(x^2+4*x+3);
diff(f,4)
%%
%如何求解100阶导数
tic,F=diff(f,100);toc2.Matlab语言的优越性
%%
%MATLAB的优点:
%MATLAB 语言的简洁高效性
%MATLAB 语言的科学运算功能
%MATLAB 语言的绘图功能
%MATLAB 庞大的工具箱与模块集
%MATLAB 强大的动态系统仿真功能3.Matlab语言变量声明规则
%%
%MATLAB语言的变量与常量:变量定义和常见的编程语言类似
%uint8,常用于图像表示和处理,8位
%int8(),int16(),int32(),uint16(),uint32()
%变量声明:syms/var_list/var_props
%显示符号变量精度:vpa(A)
%默认精度:32位小数对应的应用:vpa()函数求解pi的300有效数字:
%%
%求出pi的300位有效数字
vpa(pi,300)4.Matlab矩阵的使用规则
4.1.矩阵的表示和输出
%%
%矩阵A的表示
A=[1,2,3;4,5,6;7,8,9]
A=[[A;[1 2 3]],[1;2;3;4]]
%ans=[[1,2,3,1],[4,5,6,2],[7,8,9,3][1,2,3,4]]
%%
%冒号表达式:v=s1:s2:s3 s1起始 s3终止,s2步长
v1=0:0.2:pi
%v2=0:-0.1:pi
v3=0:pi%默认步长为1
v4=pi:-0.1:0
%%
%矩阵切片,和Python类似
A=[1,2,3;4,5,6;7,8,0];
B1=A(1:2:end,:)
B2=A([3,2,1],[3,2,1])
B3=A(:,end:-1:1)4.2.矩阵的代数运算
%%
%矩阵的代数运算
%一般来说,矩阵的转置A^T=A'
%矩阵乘法A*B
%矩阵左除法AX=B=>X=A^(-1)B=A\B
%矩阵右除法XA=B=>X=BA^(-1)=B/A
%矩阵的左右翻转B=fliplr(A)
%矩阵旋转90度:D=rot90(A)
%矩阵旋转180度:D=rot90(rot90(A))
%矩阵A的x次幂:F=A^x
%矩阵的点运算C=A.*B矩阵代数运算例题:
%%
%求出矩阵A的全部三次方根,并检验结果
A=[1,2,3;4,5,6;7,8,0]
C=A^(1/3)4.3.矩阵的逻辑运算
%%
%MATLAB的矩阵逻辑运算
%与运算 A&B
%或运算 A|B
%非运算 B=~A
%异或运算 xor(A,B)矩阵逻辑预算例题:
%%
%矩阵的比较运算
A=[1,2,8; 4,5,2; 7,8,0];
A
B=find(A>5)%返回符合条件的矩阵下标,竖着看。
%%
A
[i,j]=find(A>5)
%%
%all函数检测矩阵是否全为非零元素 是返回1 不是返回0
%any函数检测矩阵是否存在非零元素 是返回1 不是返回0
a1=all(A>=5),a2=any(A>=5)4.4.矩阵的化简与变换
%%
%MATLAB解析结果的化简与变换
%collect()合并同类项
%expand()展开多项式
%factor()因式分解矩阵的化简与变换例题:
%%
syms s;
P=(s+3)^2*(s^2+3*s+2)*(s^3+12*s^2+48*s+64)
P1=simplify(P)%simple函数不能使用
P3=expand(P)
%%
%MATLAB变量替换语句
syms x;
syms x1;
f=x+3;
f1=subs(f,x,x1)
f1=latex(f)
5.部分例题代码
5.1.Hilbert矩阵构造
%%
%例题:2.10假设3x3的Hilbert矩阵可以由定义A=hilb(3),试对其进行有理数变换
A=hilb(3)
[n,d]=rat(A)%返回n./d的值5.2.求解公约数和公倍数
%%
%例题2.11:试求1856120和1483720的最大公约数与最小公倍数,并求出所得出的最小公倍数的质因数分解。
n=sym(1856120);
m=sym(1483720)
gcd(m,n)%最大公约数
lcm(m,n)%最小公倍数
factor(lcm(m,n))5.3.寻找1-1000的质数
%%
%例2.12:试求出1~1000间的全部质数
A=1:1000;
B=A(isprime(A))6.Matlab的循环结构例题
6.1.求1-100之和
%%
%例2.13:循环结构for
s1=0;
for i=1:100
s1=s1+i;
end
s1
%%
%循环结构:while
s2=0;
i=1;
while(i<=100)
s2=s2+i;
i=i+1
end
s2
%%
%更加简单的sum函数
sum(1:100)6.2.求解最小m值
%%
%例2.14:用循环求解求最小的 m,使下式成立
sum=0;
i=1
while(sum<1000)
sum=sum+i
i=i+1
end
sum
i6.3.循环求和
%%
%例2.15
sum=0;
for i=1:100000
sum=sum+1/(2^i)+1/(3^i);
end
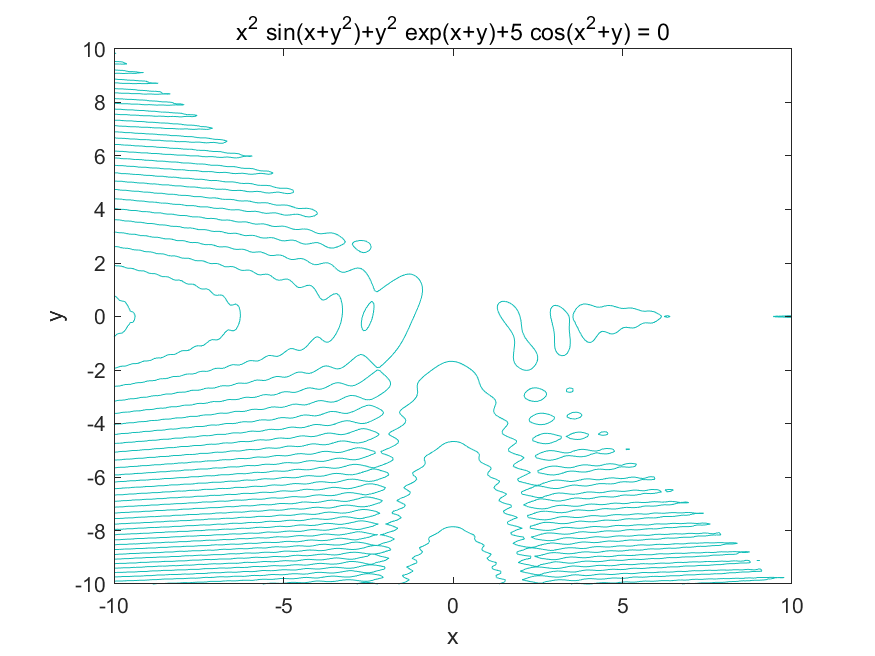
sum7.绘制隐函数
%%
%绘制隐函数
ezplot('x^2*sin(x+y^2)+y^2*exp(x+y)+5*cos(x^2+y)',[-10,10])
saveas(gcf,['C:\Users\Zeng Zhong Yan\Desktop\MATLAB\','隐函数','.png'])