梯度
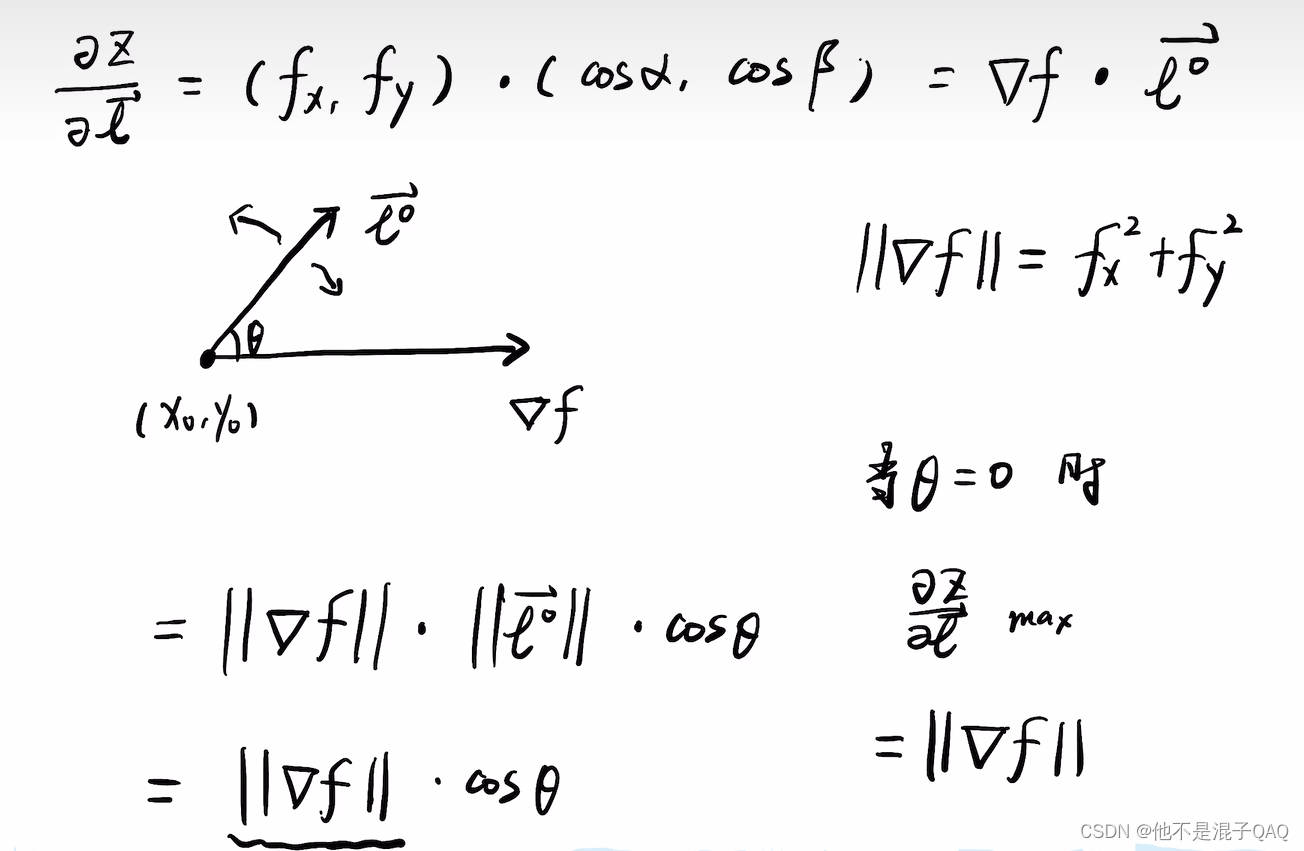
最优化理论
最优化基础---基本概念：凸优化、梯度、Jacobi矩阵、Hessian矩阵_哔哩哔哩_bilibili
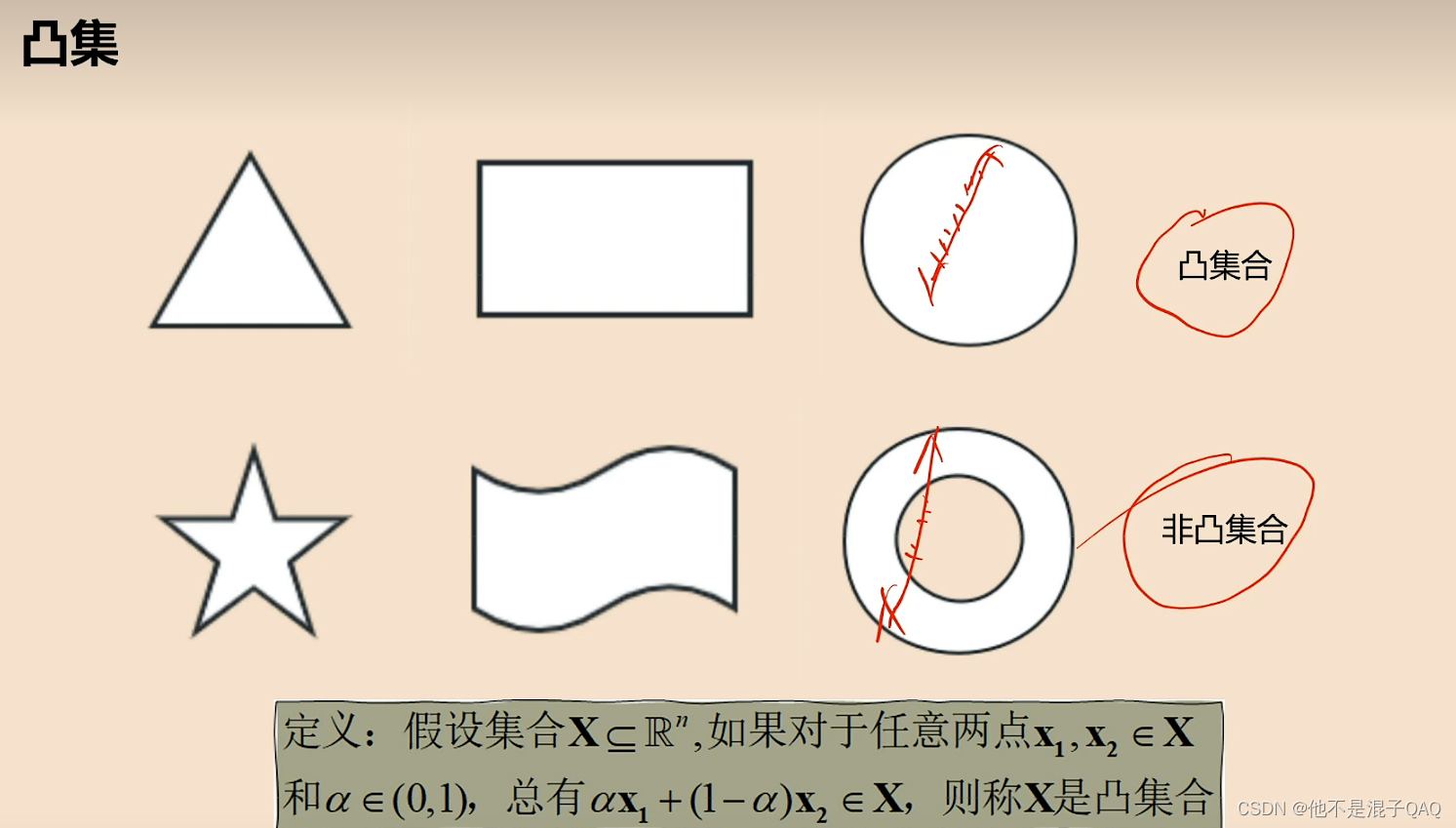从图像来看：存在两点连线上的点不在集合内
定义 ax1+(1-a)x2 其实就是两点连线上的点
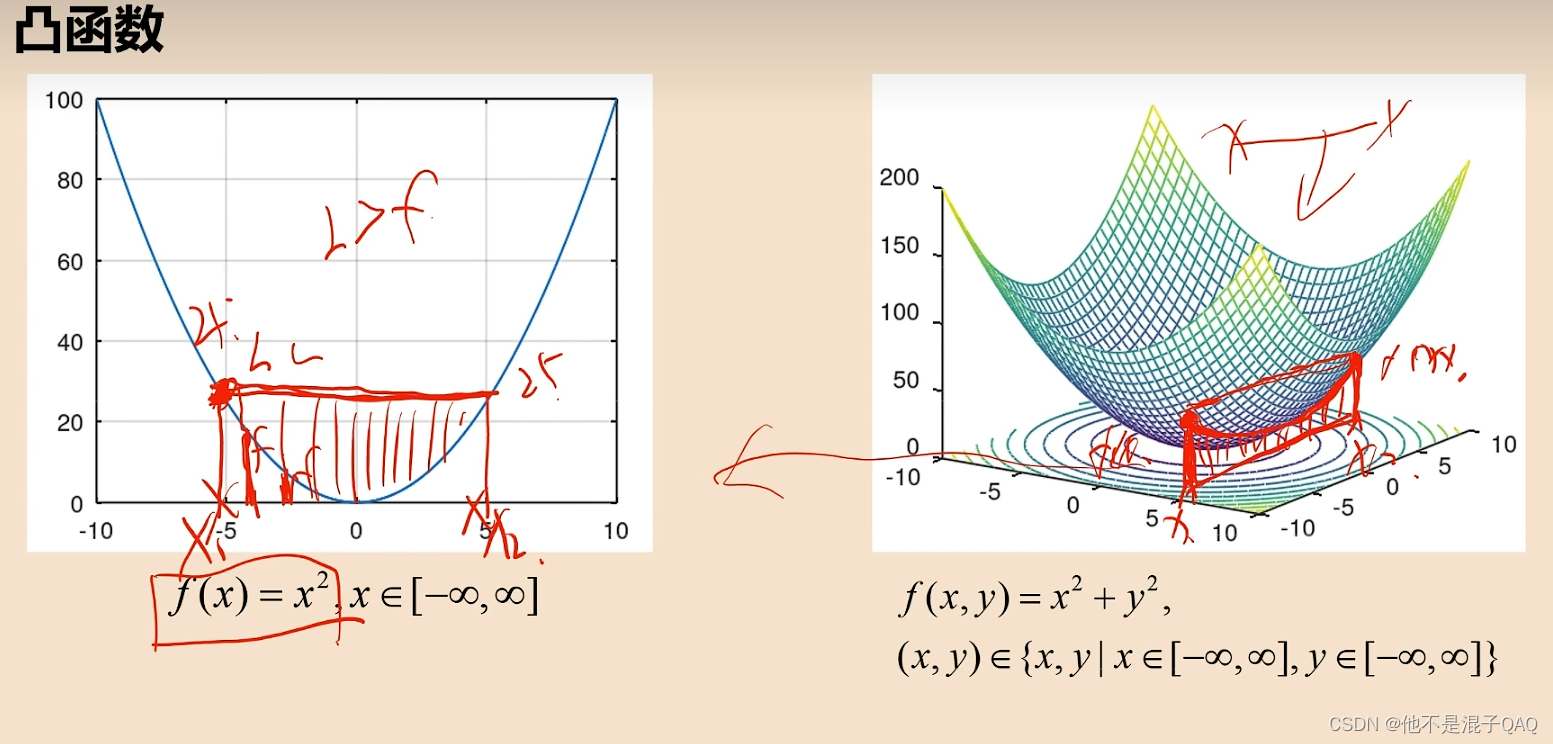
可用 与函数围成的面积 和 与坐标轴围成的面积 角度理解凸函数
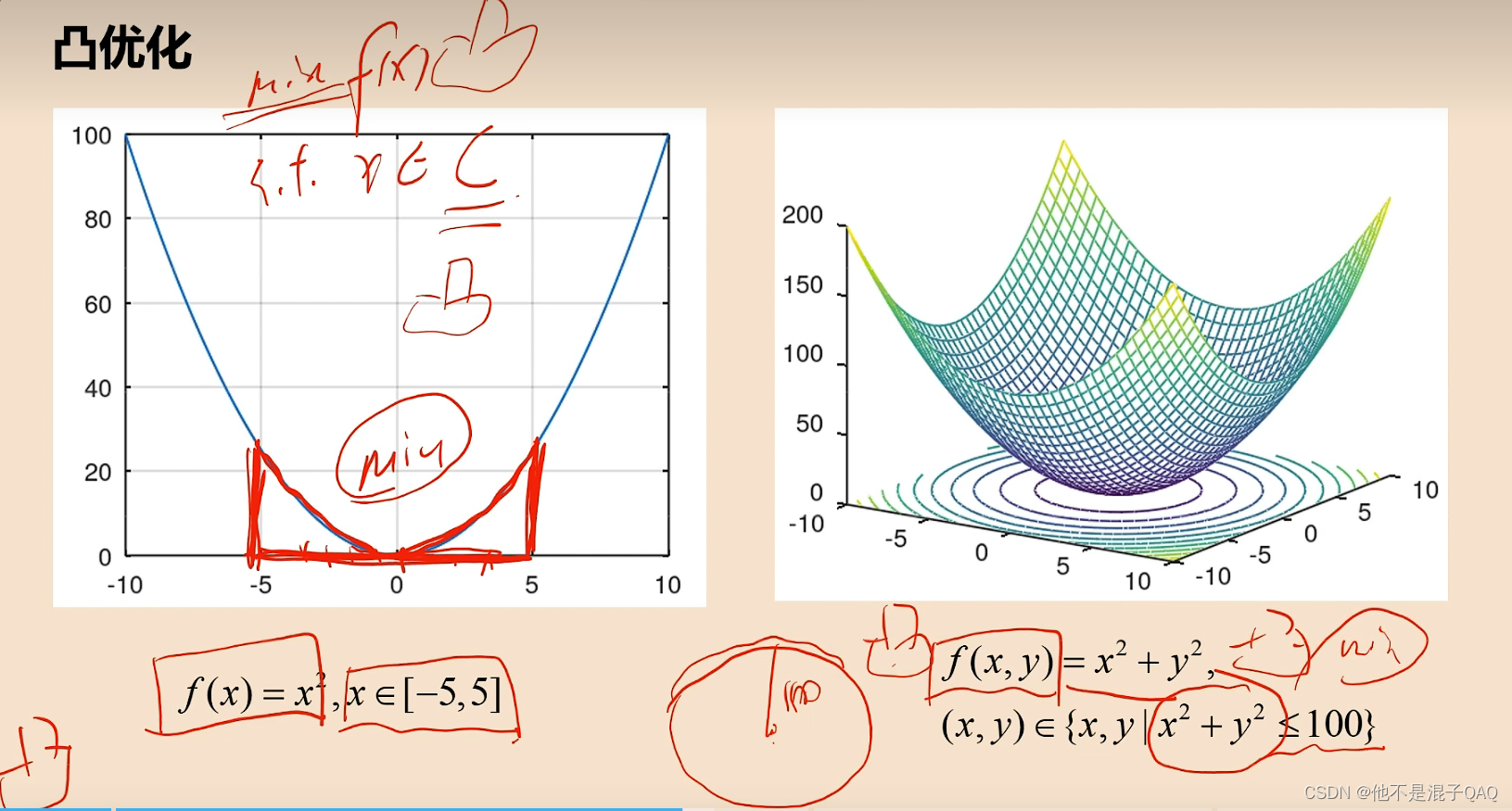
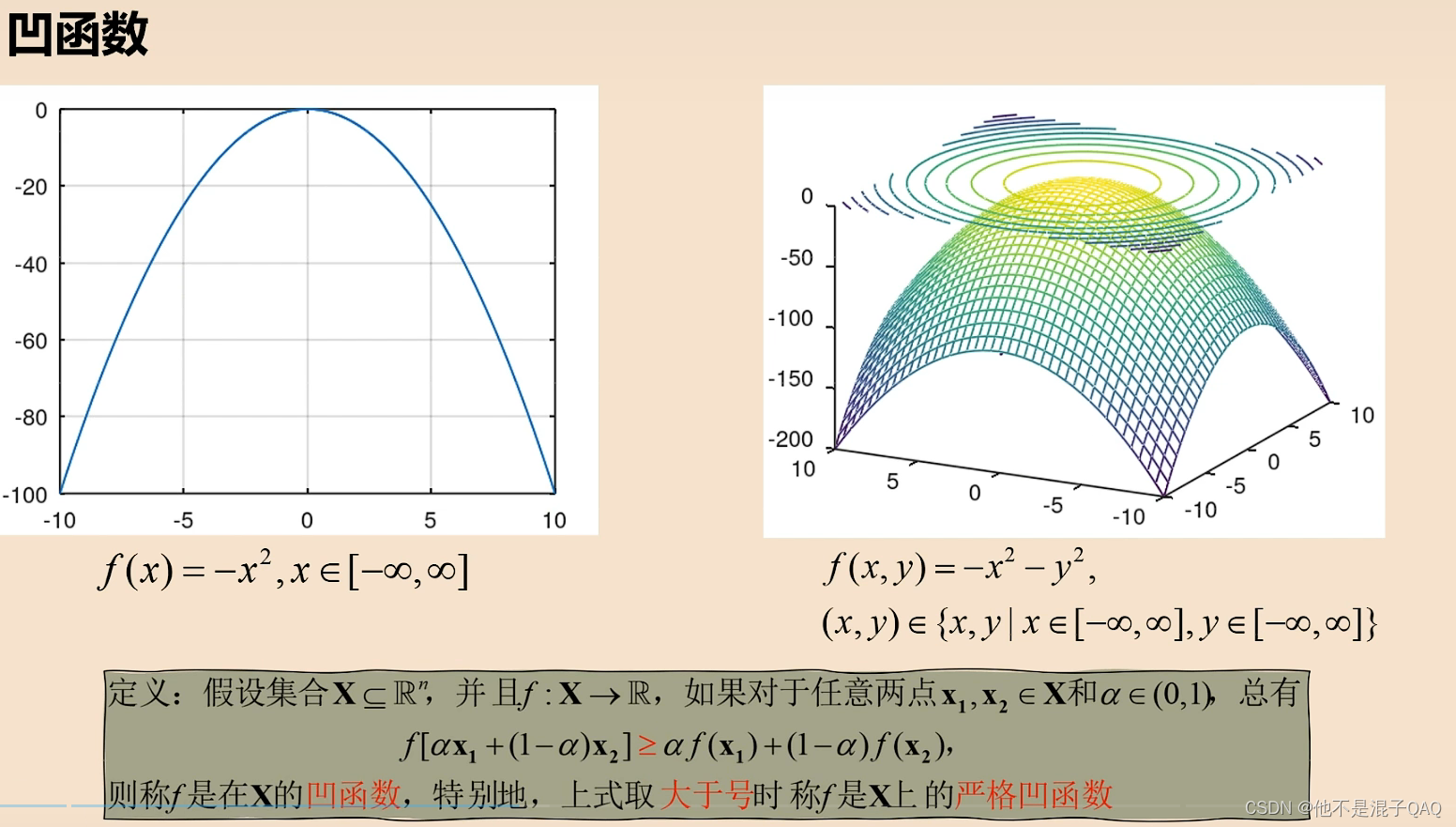凸优化
在定义域和F（X)都是凸集的问题（凸凸问题），就是凸优化
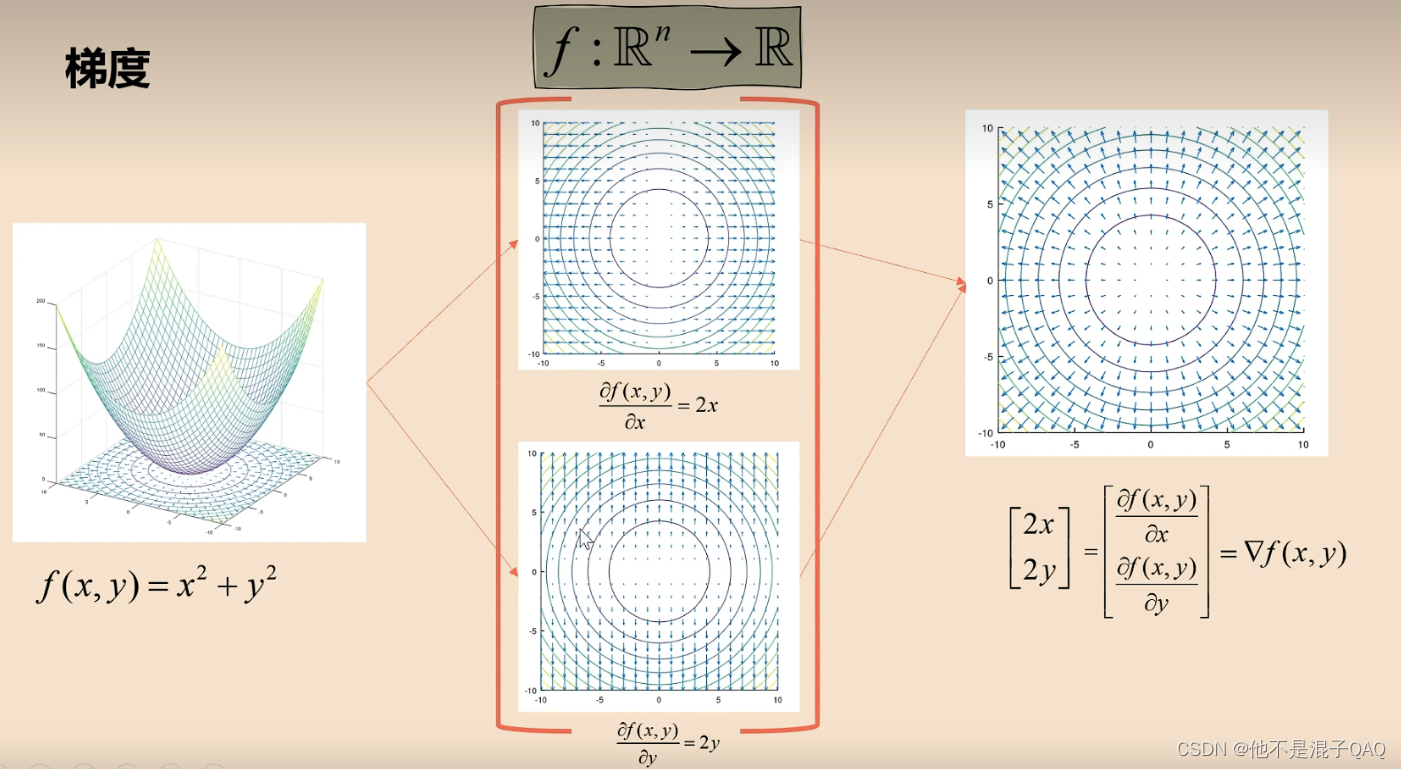
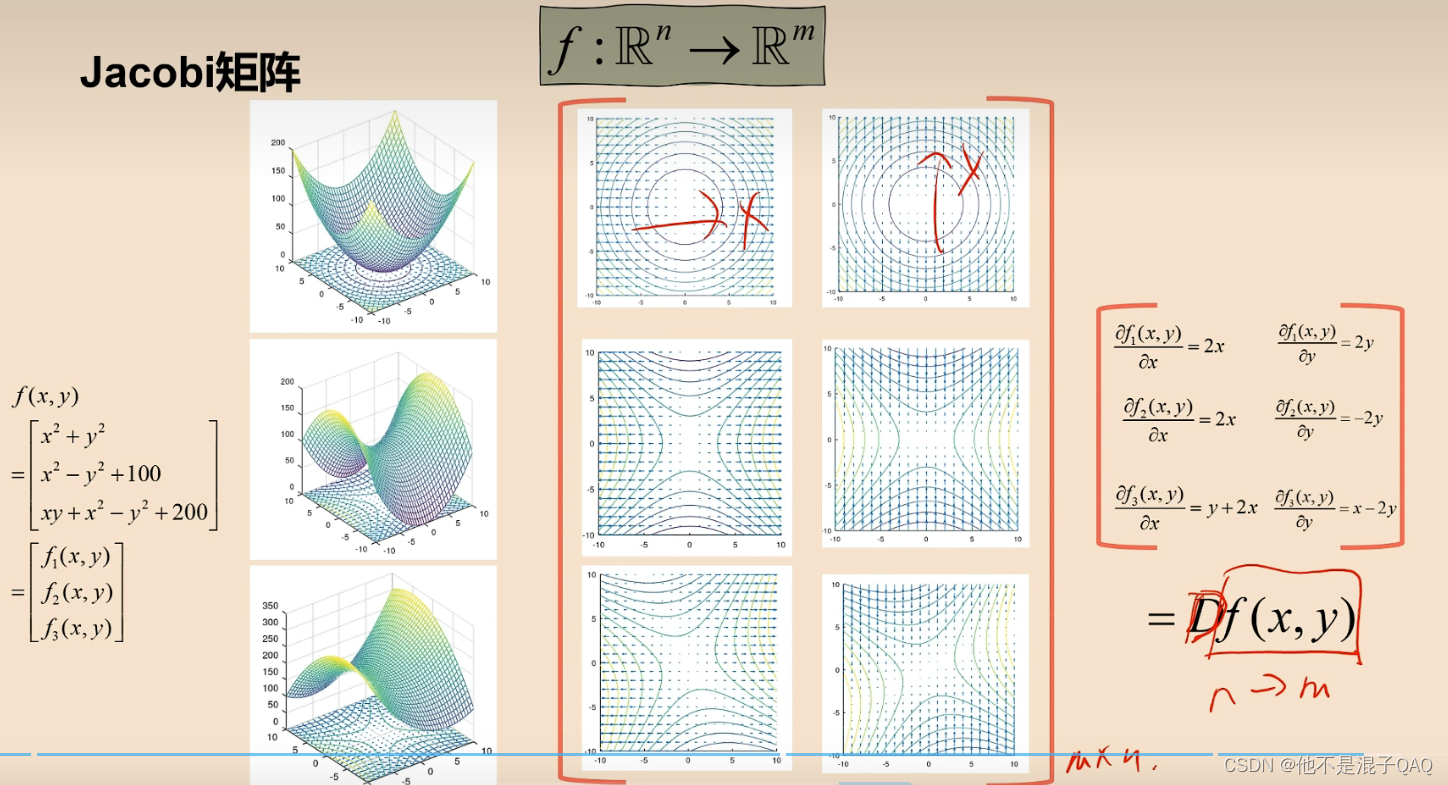jacobi 广义导数 n维映射到m维
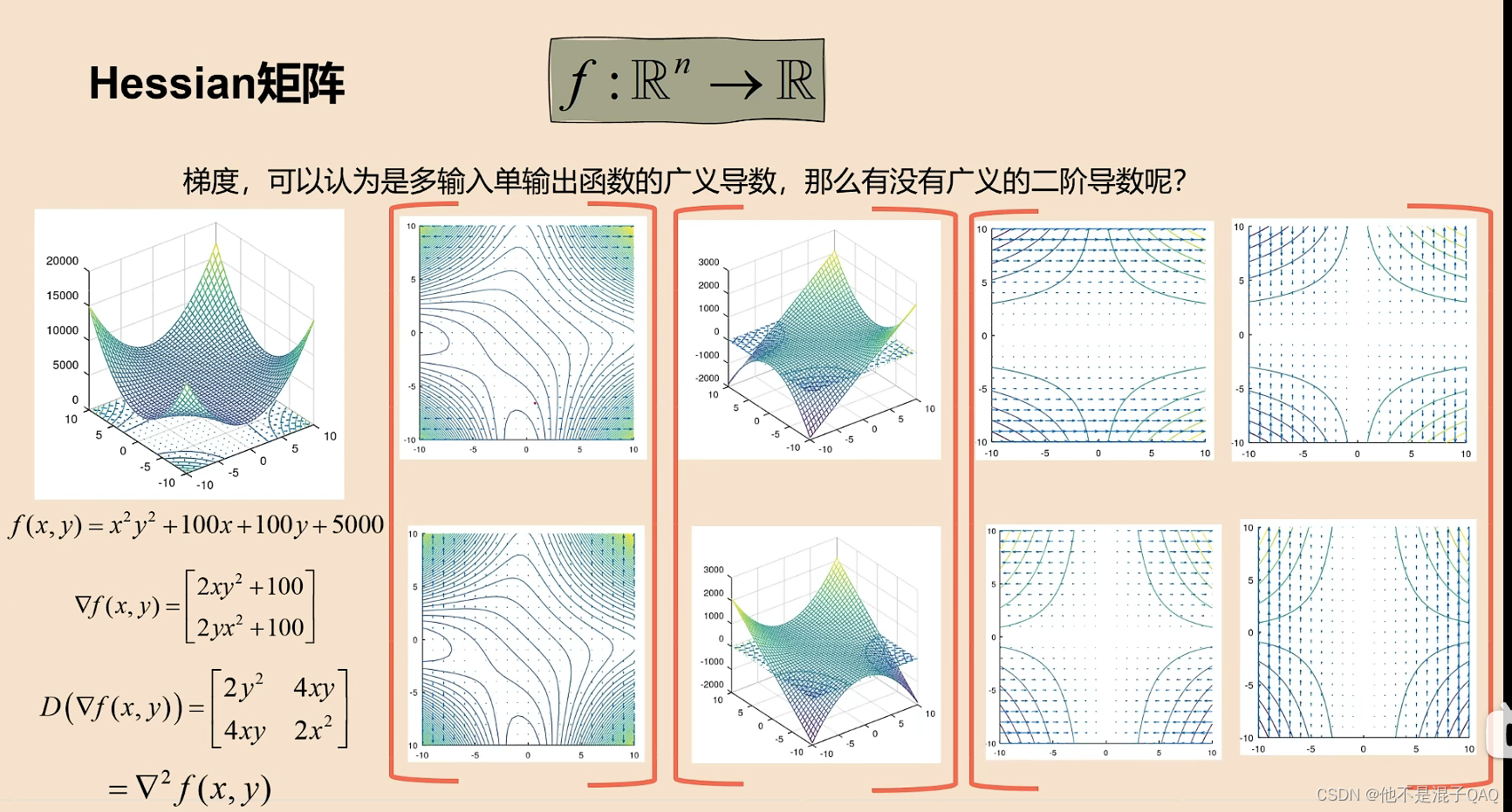梯度的雅可比矩阵就是海森矩阵
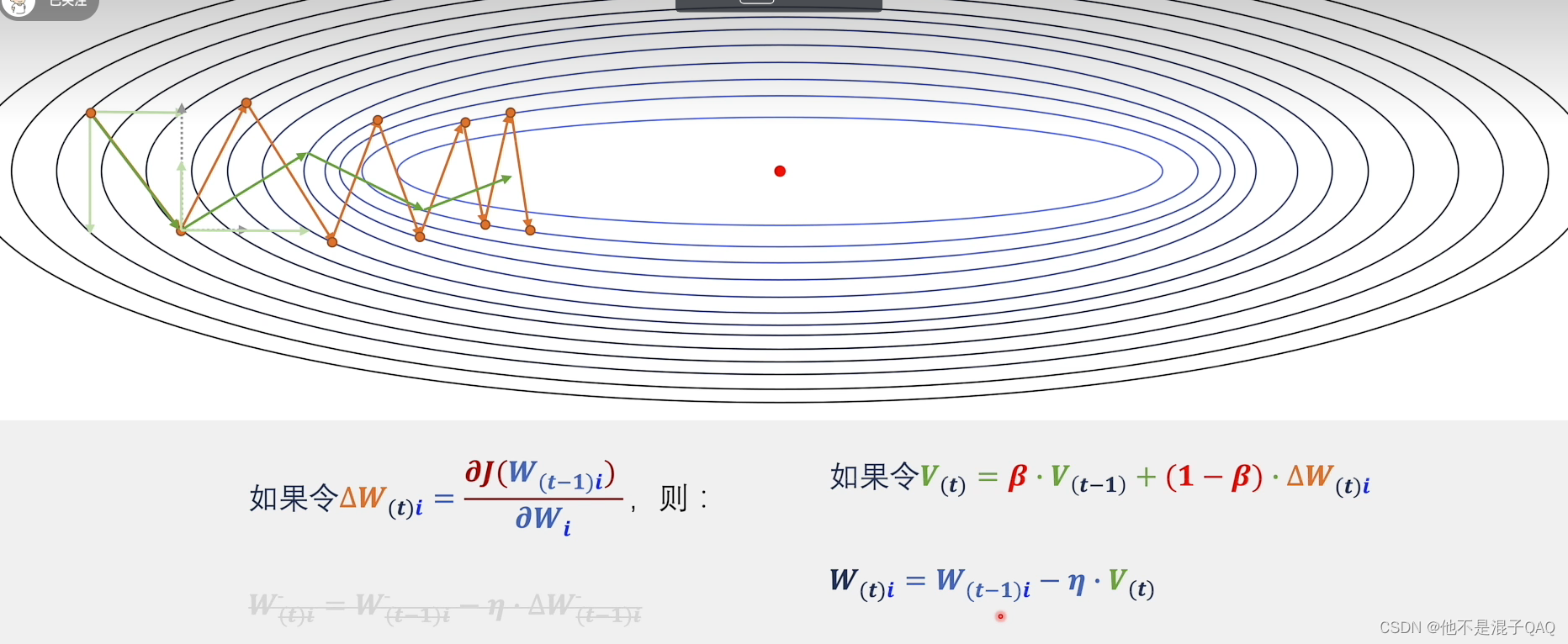
动量法（Momentum）是一种常用的梯度下降优化算法，通过引入动量概念来加速收敛速度和提高稳定性。在传统的梯度下降算法中，每次更新参数时都是直接根据当前的梯度进行更新，而动量法则考虑了之前的更新历史，使得参数更新更具有惯性。
动量法的核心思想是在更新参数时，根据当前的梯度和之前累积的速度（动量），计算出新的速度，并利用新的速度来更新参数。其计算方式如下：
v(t) = β * v(t-1) + (1 - β) * ∇J(w)
w(t) = w(t-1) - α * v(t)
其中，v(t)表示当前时刻的速度，w(t)表示当前时刻的参数，∇J(w)表示当前时刻的梯度，α为学习率（步长），β为动量系数，控制了之前速度的权重。
动量法的关键在于动量系数的选择。动量系数越大，之前速度对当前速度的影响就越大，可以增加算法在平坦区域的探索能力，减少震荡；动量系数越小，算法则更加稳定，适合处理局部极小值点。
动量法的优点是可以加速收敛速度、提高稳定性，并且在处理具有大量平坦区域的目标函数时特别有效。它广泛应用于深度学习和神经网络的训练过程中，能够加速模型的收敛，提高训练效率。
牛顿法
牛顿法（Newton's Method），是一种用于求解方程的迭代数值方法。它通过使用函数的一阶和二阶导数信息，以迭代的方式逼近方程的根。
牛顿法的基本原理如下：
初始化：选择一个初始近似解 x₀。
迭代过程：
- 计算当前近似解 xₙ 的函数值 f(xₙ) 和一阶导数值 f'(xₙ)。
- 如果 f'(xₙ) ≈ 0，则终止迭代，xₙ 可能是方程的驻点。
- 更新近似解：xₙ₊₁ = xₙ - f(xₙ) / f'(xₙ)。
判断条件：
- 若 |xₙ₊₁ - xₙ| < ε，其中 ε 为预先设定的精度要求，迭代收敛，结束迭代过程。
- 否则，重复步骤 2，直到满足终止条件。
牛顿法利用了函数的局部线性近似来寻找方程根，通过不断迭代更新近似解，使得近似解逐渐接近真实的根。相比于区间消去法，牛顿法在附近具有较好的收敛速度，尤其适用于平坦区域较小的光滑函数。
牛顿法在求解非线性方程、优化问题以及曲线拟合等领域广泛应用。然而，牛顿法也有一些局限性，如对于初始近似解的选择敏感，可能出现迭代发散或跳过根的情况。此外，在某些情况下，牛顿法可能会陷入局部最小值或不稳定的状态。
为了克服牛顿法的局限性，人们发展了许多改进的变体方法，如拟牛顿法（Quasi-Newton Methods）和加权牛顿法（Weighted Newton Methods），以提高算法的稳定性和收敛性。
牛顿法得知道一阶导、二阶导。简直天上掉馅饼，而插值法使用导数的定义代替牛顿法中二阶导。
