数据结构之堆的结构与实现

2023-09-18 22:19:13

目录

一、堆的概念及结构

1.1堆的概念

 1.2堆的性质

1.3堆的结构

二、堆的实现

2.1堆向下调整算法（父亲与孩子做比较）

 2.2堆的向上调整算法（孩子与父亲做比较）

2.3堆的创建（向下建堆）

 2.4向下建堆的时间复杂度

2.5堆的插入

2.6堆的删除

2.7堆的完整代码实现

三、堆的应用

3.1堆排序

3.2TOP-K问题

 

一、堆的概念及结构

1.1堆的概念

 1.2堆的性质

堆中某个节点的值总是不大于或不小于其父节点的值；

堆总是一棵完全二叉树。

1.3堆的结构

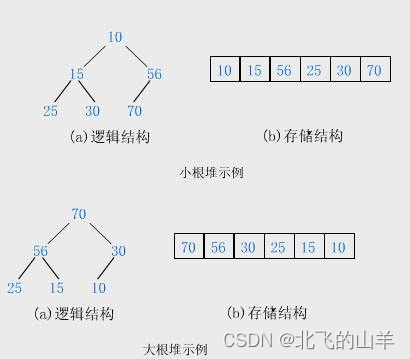
二、堆的实现

2.1堆向下调整算法（父亲与孩子做比较）

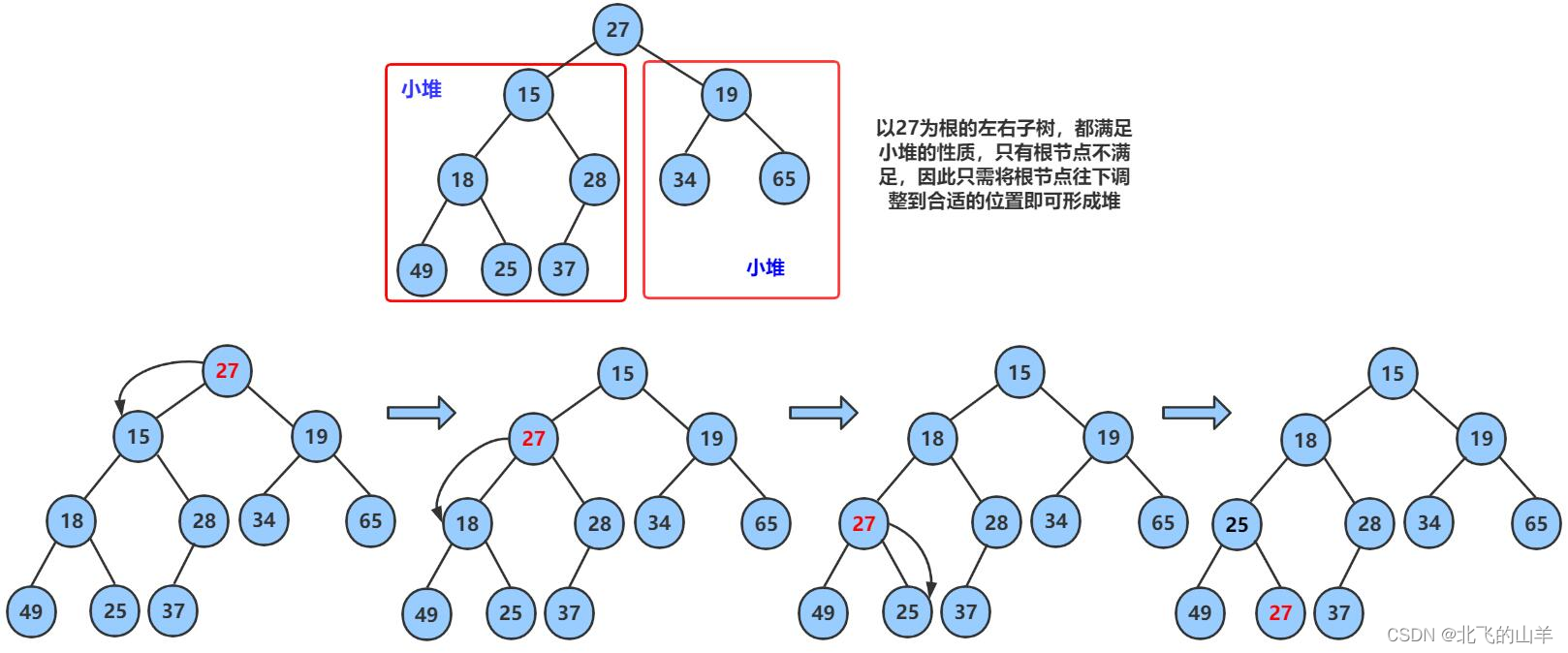
我们给出一个数组，逻辑上看做一颗完全二叉树。我们通过从根节点开始的向下调整算法可以把它调整成一个小堆。向下调整算法有一个前提：左右子树必须是一个堆，才能调整。
以下面图片为例：建小堆过程中父亲不断与较小的孩子交换

用代码来实现：

void AdjustDown(HPDataType* a, int n, int parent)//n是参与向下算法的元素的个数
{
	int child = parent * 2 + 1;
	while (child < n)
	{
		//建小堆，找到两个孩子中较小的那一个
		if (child + 1 < n && a[child + 1] < a[child])
		{
			child++;
		}
		//如果父亲不比孩子大，就证明已经是小堆了，直接跳出循环；
		//如果比孩子大就一直交换
		if (a[child] < a[parent])
		{
			Swap(&a[child], &a[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
			break;
	}
}

 2.2堆的向上调整算法（孩子与父亲做比较）

代码实现如下：

void AdjustUp(HPDataType* a, int child)
{
	int parent = (child - 1) / 2;
	while (child > 0)
	{
		if (a[child] < a[parent])
		{
			Swap(&a[child], &a[parent]);
			child = parent;
			parent = (child - 1) / 2;
		}
		else
			break;
	}
}

2.3堆的创建（向下建堆）

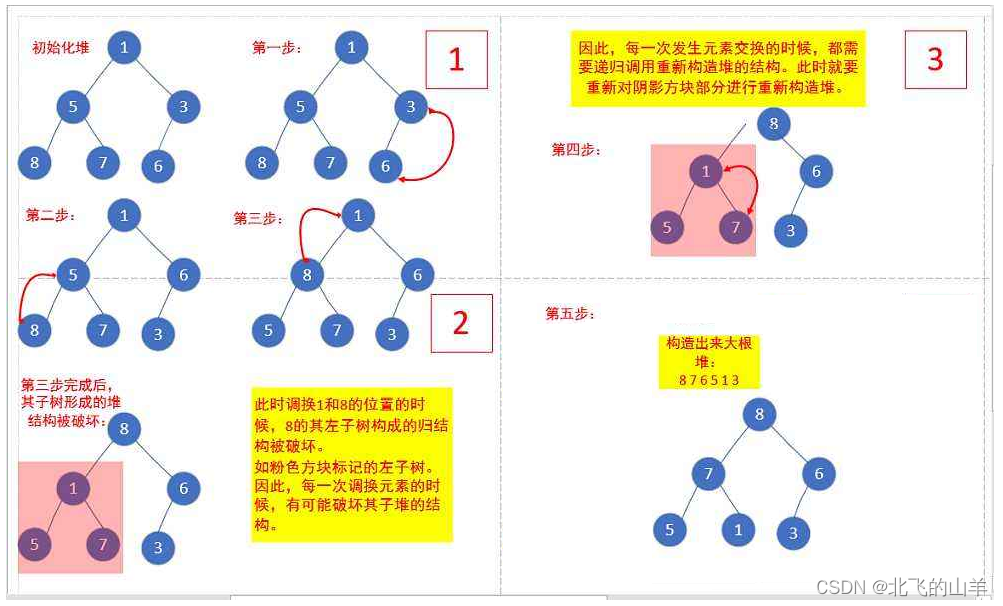
我们给出一个数组，这个数组逻辑上可以看做一颗完全二叉树，但是还不是一个堆，现在我们通过算法，把它构建成一个堆。根节点左右子树不是堆，我们怎么调整呢？这里我们从倒数的第一个非叶子节点的 子树开始调整（向下调整），一直调整到根节点的树，就可以调整成堆。
假定有数组 int a [] = { 1 , 5 , 3 , 8 , 7 , 6 };

 2.4向下建堆的时间复杂度

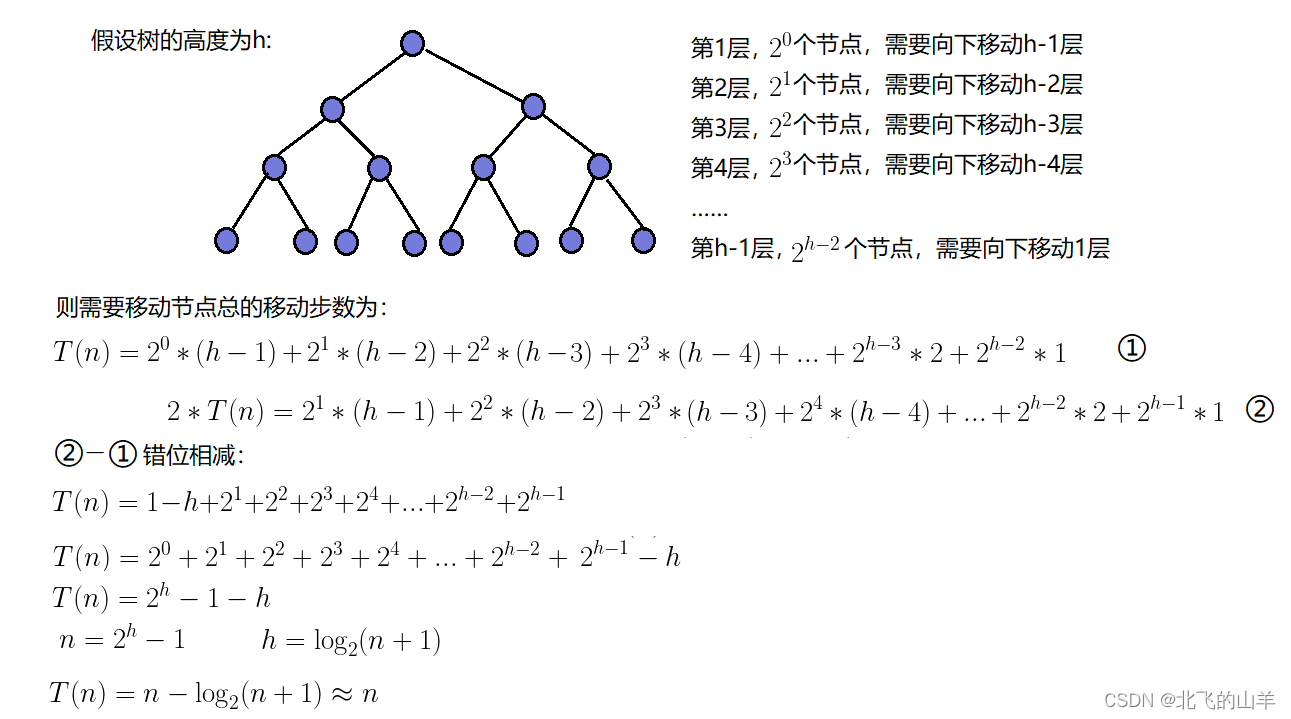
因为堆是完全二叉树，而满二叉树也是完全二叉树，此处为了简化使用满二叉树来证明 ( 时间复杂度本来看的就是近似值，多几个节点不影响最终结果 ) ：

 因此：向下建堆的时间复杂度为O(N)。

既然谈到了向下建堆的时间复杂度，不妨就算一下向上建堆的时间复杂度：

 冲两张图中可以看到：向下调整建堆的效率略高于向上调整建堆的效率，所以我上面所讨论的也都是向下调整建堆的实现方法。

2.5堆的插入

先插入一个 10 到数组的尾上，再进行向上调整算法，直到满足堆。

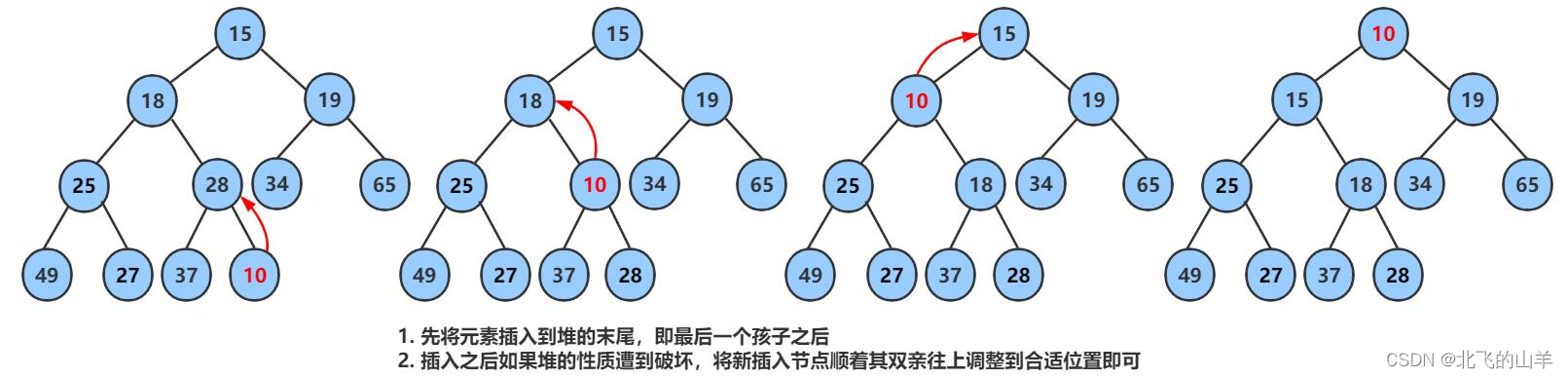
 代码实现：

void HeapPush(Heap* hp, HPDataType x)
{
	assert(hp);
	//判满以及扩容
	if (hp->_capacity == hp->_size)
	{
		int newCapacity = hp->_capacity == 0 ? 4 : 2 * hp->_capacity;
		HPDataType* tmp = (HPDataType*)realloc(hp->_a, sizeof(HPDataType) * newCapacity);
		
		if (tmp == NULL)
		{
			perror("realloc fail");
			exit(-1);
		}
		hp->_a = tmp;
		hp->_capacity = newCapacity;
	}
	hp->_a[hp->_size] = x;
	hp->_size++;

	AdjustUp(hp->_a, hp->_size - 1);
}

2.6堆的删除

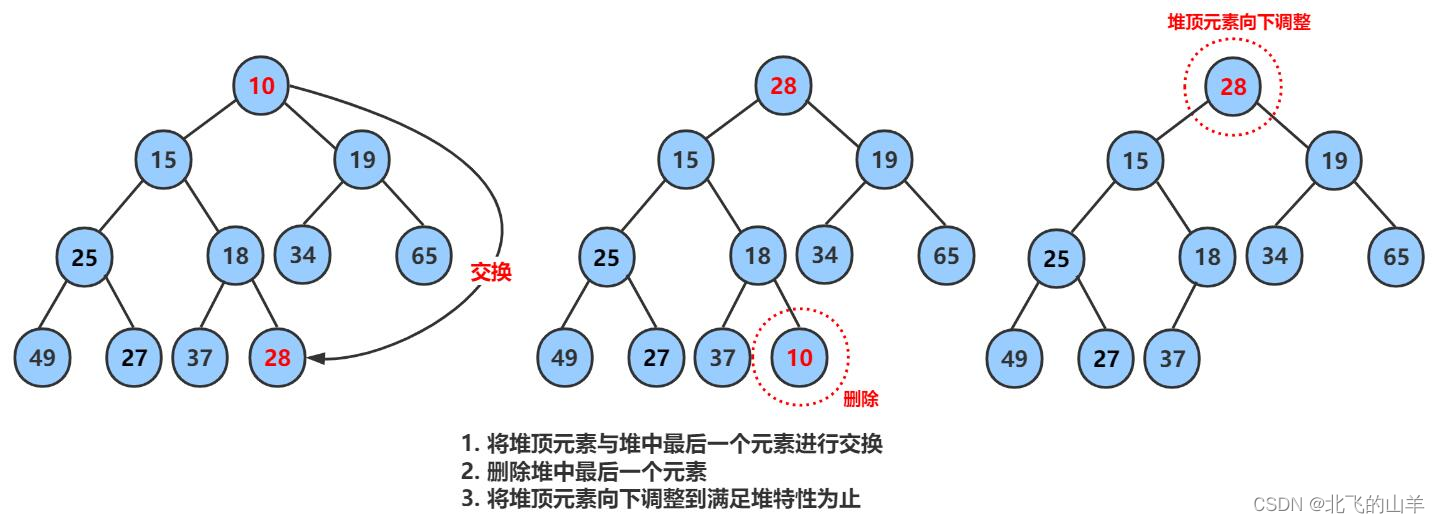
删除堆是删除堆顶的数据，将堆顶的数据根最后一个数据一换，然后删除数组最后一个数据，再进行向下调整算法。

 代码实现：

void HeapPop(Heap* hp)
{
	assert(hp);
	assert(hp->_size > 0);

	Swap(&hp->_a[0], &hp->_a[hp->_size - 1]);
	hp->_size--;
	AdjustDown(hp->_a, hp->_size, 0);
}

2.7堆的完整代码实现

//Heap.h

#pragma once

#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include <string.h>

typedef int HPDataType;
typedef struct Heap
{
	HPDataType* _a;
	int _size;
	int _capacity;
}Heap;

//堆的初始化
void HeapInit(Heap* hp);

// 堆的构建
void HeapCreate(Heap* hp, HPDataType* a, int n);

//交换
void Swap(HPDataType* a, HPDataType* b);

//向上调整
void AdjustUp(HPDataType* a, int child);

//向下调整
void AdjustDown(HPDataType* a, int n, int parent);

//打印
void HeapPrint(Heap* hp);

// 堆的销毁
void HeapDestory(Heap* hp);

// 堆的插入
void HeapPush(Heap* hp, HPDataType x);

// 堆的删除
void HeapPop(Heap* hp);

// 取堆顶的数据
HPDataType HeapTop(Heap* hp);

// 堆的数据个数
int HeapSize(Heap* hp);

// 堆的判空
int HeapEmpty(Heap* hp);
//Heap.c
#include "Heap.h"

void HeapInit(Heap* hp)
{
	assert(hp);
	hp->_a = NULL;
	hp->_capacity = 0;
	hp->_size = 0;
}

void HeapCreate(Heap* hp, HPDataType* a, int n)
{
	assert(hp);
	assert(a);
	hp->_a = (HPDataType*)malloc(sizeof(HPDataType)*n);

	if (hp->_a == NULL)
	{
		perror("malloc fail");
		exit(-1);
	}
	hp->_capacity = n;
	hp->_size = n;

	memcpy(hp->_a, a, sizeof(HPDataType) * n);

	for (int i = 1; i < n; i++)
	{
		AdjustUp(hp->_a, i);
	}
}

void Swap(HPDataType* a, HPDataType* b)
{
	HPDataType tmp = *a;
	*a = *b;
	*b = tmp;
}

void AdjustUp(HPDataType* a, int child)
{
	int parent = (child - 1) / 2;
	while (child > 0)
	{
		if (a[child] < a[parent])
		{
			Swap(&a[child], &a[parent]);
			child = parent;
			parent = (child - 1) / 2;
		}
		else
			break;
	}
}

void AdjustDown(HPDataType* a, int n, int parent)//n是参与向下算法的元素的个数
{
	int child = parent * 2 + 1;
	while (child < n)
	{
		//建小堆，找到两个孩子中较小的那一个
		if (child + 1 < n && a[child + 1] < a[child])
		{
			child++;
		}
		//如果父亲不比孩子大，就证明已经是小堆了，直接跳出循环；
		//如果比孩子大就一直交换
		if (a[child] < a[parent])
		{
			Swap(&a[child], &a[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
			break;
	}
}

void HeapDestory(Heap* hp)
{
	assert(hp);
	free(hp->_a);
	hp->_capacity = 0;
	hp->_size = 0;
}

void HeapPush(Heap* hp, HPDataType x)
{
	assert(hp);
	//判满以及扩容
	if (hp->_capacity == hp->_size)
	{
		int newCapacity = hp->_capacity == 0 ? 4 : 2 * hp->_capacity;
		HPDataType* tmp = (HPDataType*)realloc(hp->_a, sizeof(HPDataType) * newCapacity);
		
		if (tmp == NULL)
		{
			perror("realloc fail");
			exit(-1);
		}
		hp->_a = tmp;
		hp->_capacity = newCapacity;
	}
	hp->_a[hp->_size] = x;
	hp->_size++;

	AdjustUp(hp->_a, hp->_size - 1);
}

void HeapPrint(Heap* hp)
{
	assert(hp);
	for (int i = 0; i < hp->_size; i++)
	{
		printf("%d ", hp->_a[i]);
	}
	printf("\n");
}

void HeapPop(Heap* hp)
{
	assert(hp);
	assert(hp->_size > 0);

	Swap(&hp->_a[0], &hp->_a[hp->_size - 1]);
	hp->_size--;
	AdjustDown(hp->_a, hp->_size, 0);
}

HPDataType HeapTop(Heap* hp)
{
	assert(hp);
	assert(hp->_size > 0);
	return hp->_a[0];
}

int HeapSize(Heap* hp)
{
	return hp->_size;
}

int HeapEmpty(Heap* hp)
{
	assert(hp);
	if (hp->_size == 0)
		return 0;
	else
		return 1;
}

三、堆的应用

3.1堆排序

堆排序即利用堆的思想来进行排序，总共分为两个步骤：
1. 建堆：
升序：建大堆，降序：建小堆。
2. 利用堆删除思想来进行排序
建堆和堆删除中都用到了向下调整，因此掌握了向下调整，就可以完成堆排序。
具体实现代码如下： 
void HeapSort1(int* a, int n)
{
	//向上调整建堆
	/*for (int i = 1; i < n; i++)
	{
		AdjustUp(a, i);
	}*/
	//向下调整建堆
	for (int i = (n - 1 - 1) / 2; i >= 0; i--)//从第一个非叶子节点开始向下调整
	{
		AdjustDown(a, n, i);
	}

	//排序
	int end = n - 1;
	while (end)
	{
		Swap(&a[0], &a[end]);
		AdjustDown(a, end, 0);
		end--;
	}
}

3.2TOP-K问题

TOP-K问题：即求数据结合中前K个最大的元素或者最小的元素，一般情况下数据量都比较大。

对于 Top-K 问题，能想到的最简单直接的方式就是排序，但是：如果数据量非常大，排序就不太可取了 ( 可能数据都不能一下子全部加载到内存中 ) 。最佳的方式就是用堆来解决，基本思路如下：
1. 用数据集合中前 K 个元素来建堆 :
前 k 个最大的元素，则建小堆，前 k 个最小的元素，则建大堆 。
2. 用剩余的 N-K 个元素依次与堆顶元素来比较，不满足则替换堆顶元素
将剩余 N-K 个元素依次与堆顶元素比完之后，堆中剩余的 K 个元素就是所求的前 K 个最小或者最大的元素。
具体实现代码如下： 
void CreatNData()
{
	// 造数据
	int n = 10000000;
	srand(time(0));
	const char* file = "data.txt";
	FILE* fin = fopen(file, "w");
	if (fin == NULL)
	{
		perror("fopen error");
		return;
	}
	//将数据写入data文件中
	for (int i = 0; i < n; ++i)
	{
		int x = (rand() + i) % 10000000;
		fprintf(fin, "%d\n", x);
	}

	fclose(fin);
}


void PrintTopK(const char* filename, int k)
{
	FILE* fout = fopen(filename, "r");
	if (fout == NULL)
	{
		perror("fopen fail");
		exit(-1);
	}
	int* minHeap = (int*)malloc(sizeof(int) * k);
	if (minHeap == NULL)
	{
		perror("malloc fail");
		return;
	}
	for (int i = 0; i < k; i++)
	{
		fscanf(fout, "%d", &minHeap[i]);
	}
	for (int i = (k - 1 - 1) / 2; i >= 0; i--)
	{
		AdjustDown(minHeap, k, i);
	}
	//将剩余的n-k各元素与堆顶的元素进行交换
	int x = 0;
	while (fscanf(fout, "%d", &x) != EOF)
	{
		if (x > minHeap[0])
		{
			minHeap[0] = x;
			AdjustDown(minHeap, k, 0);
		}
	}


	//排序
	int end = k - 1;
	while (end)
	{
		Swap(&minHeap[0], &minHeap[end]);
		AdjustDown(minHeap, end, 0);
		end--;
	}

	for (int i = 0; i < k; i++)
	{
		printf("%d ", minHeap[i]);
	}
	free(minHeap);
	fclose(fout);
}

更多推荐

Lua 多返回值

Lua这门神奇的语言可以在函数里面返回多个值具体函数如下functionmulti_return()return2,"hellowworld"endlocala,b=multi_return();--多个都返回print(a,b)localm=multi_return();--默认返回第一个返回值print(m)unp

搭建Flink集群、集群HA高可用以及配置历史服务器

Flink集群搭建Flink集群搭建集群规划下载并解压安装包修改集群配置分发安装目录启动集群访问WebUIFlink集群HA高可用概述集群规划配置flink配置master、workers配置ZK分发安装目录启动HA集群测试Flink参数配置配置历史服务器概述配置启动、停止历史服务器提交一个Job任务查看历史Job信息

数据结构上机练习——单链表的基本操作、头文件、类定义、main函数、多种链表算法的实现，含注释

文章目录单链表的基本操作实现1.头文件2.类定义和多种算法的实现2.1创建空表2.2头插法创建n个元素的线性链表2.3一个带头节点的链表存放一组整数，设计一个算法删除值等于x的所有节点。2.4计算线性表中值为偶数的节点个数2.5一个带头节点的单链表heada存放一组整数，设计分裂heada算法，偶数放在heada中，奇

二叉树的概念、存储及遍历

一、二叉树的概念1、二叉树的定义二叉树（binarytree）是n个结点的有限集合，该集合或为空集（空二叉树），或由一个根结点与两棵互不相交的，称为根结点的左子树、右子树的二叉树构成。二叉树的特点是：（1）每个结点最多有两棵子树，故二叉树中不存在度大于2的结点。（2）二叉树是有序的，其次序不能任意颠倒，即使树中的某个结

利用Socks5代理IP加强跨界电商爬虫的网络安全

随着跨界电商的兴起，爬虫技术在这个领域变得越来越重要。然而，网络安全一直是一个值得关注的问题。在本文中，我们将讨论如何利用代理IP和Socks5代理来增强跨界电商爬虫的网络安全，确保稳定和可靠的数据采集，同时避免封禁和风险。背景跨界电商是一个竞争激烈的领域，市场上的商品信息和价格常常会变动。为了保持竞争力，电商企业需要

CFGPT: Chinese Financial Assistant with Large Language Model

本文是LLM系列文章，针对《CFGPT:ChineseFinancialAssistantwithLargeLanguageModel》的翻译。CFGPT：大型语言模型的中文财务助理摘要1引言2相关工作3数据集4模型和训练5应用6结论摘要大型语言模型（LLM）在金融领域的自然语言处理任务中显示出巨大的潜力。在这项工作中

医疗虚拟仿真和虚拟现实有什么区别？哪个更好？

随着我们在仿真教育中越来越多地使用新技术，区分虚拟模式的类型很重要。虚拟仿真是一个统称，用来概括术语来描述各种基于仿真的体验，从基于屏幕的平台到沉浸式虚拟现实。然而，各虚拟平台在保真度、沉浸感和临场感的水平上有很大差异。医疗教育中存在许多虚拟解决方案的空间，对于护理虚拟仿真课程来说，没有"一刀切"的模式。在此就给大家介

如何完美通过token获取用户信息（springboot）

1.什么是Token？身份验证令牌（AuthenticationToken）：在身份验证过程中，“token”可以表示一个包含用户身份信息的令牌。例如Token（JWT）是一种常见的身份验证令牌，它包含用户的身份信息（例如用户名或用户ID）以及其他相关信息，如权限或过期时间。无意义令牌token，这种一般在获取后通过n

芯片SoC设计你了解吗？

数字IC设计根据岗位性质一般包含SOC设计，前端设计，ASIC设计，逻辑设计，IP设计，CPU设计等。有人说：做IP设计就是翻译官，做SOC设计就是连连看。SoC设计是做什么的？与IP设计有什么不同？IP设计工程师每天的工作，编码，debug，接口定好了，时钟只给一个，内部不让分频。不用做过异步处理。按照公司的编码规范

js实现短信验证码一键登录

前言短信验证码一键登录是一种方便快捷的登录方式，用户只需输入手机号码，然后接收到手机短信验证码并自动填入验证码框，即可完成登录操作。本文将介绍短信验证码一键登录的原理，并给出一个简单的示例说明。短信验证码一键登录的原理用户输入手机号码：用户在登录界面输入手机号码，并点击获取验证码按钮。发送验证码：前端通过API向后端发

Linux--线程（与进程区别）

Linux线程1、线程与进程进程可以看成只有一个控制线程：一个进程同时只做一件事情。有了多个控制线程后，可以把进程设计成在同一时刻做不止一件事，每个线程各自处理独立的任务。进程是程序执行时的一个实例，是分配系统资源（CPU时间、内存等）的基本单位。进程本身不是基本运行单位，而是线程的容器。一个进程可以拥有多个线程。进程

热文推荐
  1. 如何提取视频中的音频转为mp3

    如何提取视频中的音频转为mp3？在丰富多样的视频作品中，我们常常会遇到一些引人入胜的对话和有趣的音乐变奏。不少朋友可能曾经看过那种画面与其他作品声音巧妙搭配，给人带来无比愉悦和和谐感的趣味作品。然而，很多人虽然有着相似的创作灵感，却苦于不知道如何提取所需素材。这时候我们应该寻找方法，将视频中对我们有用的音频提取处理并保

  2. 【c语言】贪吃蛇

    当我们不想学习新知识的时候，并且特别无聊，就会突然先看看别人怎么写游戏的，今天给大家分享的是贪吃蛇，所需要的知识有结构体，枚举，以及easy-x图形库的一些基本函数就完全够用了，本来我想插入游戏的音乐，但是没找到贪吃蛇的背景音乐，所以就没加，大家可以参考我之前的博文里面有如何加音乐的教程包含的头文件#include<s

  3. 大二毕设.3-网盘系统

    目录技术选型：功能概括：基本演示：实现讲解：技术选型：前端:Vue3+ElementPlus后端:SpringBoot+Mybatis-Plus+MySQL+Redis+Caffeine+FastDFS/OSS+SpringCloudStream+RocketMQ+Zookeeper功能概括：用户模块用户注册接口幂等性

  4. 探索web3.0

    先说从web1.0、web2.0、web3.0的进化之路。Web1.0，第一代互联网，静态互联网；Web1.0的核心为：平台创造、平台所有、平台控制、平台受益。Web2.0，第二代互联网，交互式互联网；Web2.0的核心为：用户创造、平台所有、平台控制、平台受益。Web3.0，第三代互联网，协议互联网；Web3.0的核

  5. 计算机专业毕业设计项目推荐06-工作室管理系统（Java+Vue+Mysql）

    工作室管理系统（JavaSpring+Vue+Mysql）**介绍****系统总体开发情况-功能模块****各部分模块实现****最后想说的****联系方式**介绍本系列(后期可能博主会统一为专栏)博文献给即将毕业的计算机专业同学们,因为博主自身本科和硕士也是科班出生,所以也比较了解计算机专业的毕业设计流程以及模式，在

  6. 云计算的未来：云原生架构和自动化运维的崭露头角

    文章目录云计算的演进云原生架构1.容器化2.微服务3.自动化部署和扩展4.故障恢复自动化运维1.基础设施即代码（IaC）2.运维自动化示例：使用Ansible自动化配置管理3.自动化监控和报警未来展望1.更多的自动化2.多云混合云3.边缘计算4.安全性结论🎉欢迎来到云计算技术应用专栏~云计算的未来：云原生架构和自动化

  7. 自动化发布npm包小记

    1.注册npm账号打开npm官网，并注册自己的npm账号2.申请AccessToken1.登录npm官网，登录成功后，点开右上角头像，并点击AccessTokens选项2.点开GenerateNewToken下拉框，点击ClassicToken(和GranularAccessToken有什么区别，请自行查验？)3.填写

  8. WPF行为

    行为是一款重用用户界面代码的更有挑战性的工具。其基本思想是：使用行为封装一些通用UI功能。如果具有适当的行为，可使用一两行XAML标记将其附加到任意元素，从而节省编写和调试代码的工作。样式提供了重用一组属性设置的实用方法。它们帮助构建一致的、组织良好的界面迈出了重要的第一步——但它们还有许多限制。问题是在典型的应用程序

  9. 多级缓存基础架构组件设计

    基础架构组件-缓存背景目的缓存架构服务层多级缓存核心流程设计1、缓存介质2、如何实现spring注解方式多级缓存如何实现缓存的永久存储又可以过期刷新，而避免缓存失效带来的一系列缓存雪崩、击穿等问题实现缓存包装类多级缓存处理器实现1、lookup(Objectkey)2、get(Objectkey)3、重头戏get(Ob