数据结构上机练习——单链表的基本操作、头文件、类定义、main函数、多种链表算法的实现，含注释

2023-09-18 19:54:36

文章目录

单链表的基本操作实现

1.头文件

  头文件和源文件分开有很多好处：可以提高编译速度、提高代码的可维护性、提高代码的可重用性和可扩展性，同时也可以使代码结构更清晰，方便代码的管理和维护。

LinkList.h

#pragma once

#include<assert.h>

//定义单链表节点
typedef struct LNode
{
	int data;
	LNode* next;

}LNode;

test.cpp

#include<iostream>
using namespace std;

#include"LinkList.h"

             

2.类定义和多种算法的实现

  （下面所有函数都默认在类中实现）

  我们以带头单向非循环链表为例:

  带头单向非循环链表是一种链表数据结构，其中每个节点包含一个数据域和一个指向下一个节点的指针域。在这种链表中，有一个特殊的节点称为头节点，它指向链表的第一个节点。头节点不是链表的一部分，仅用于方便操作。

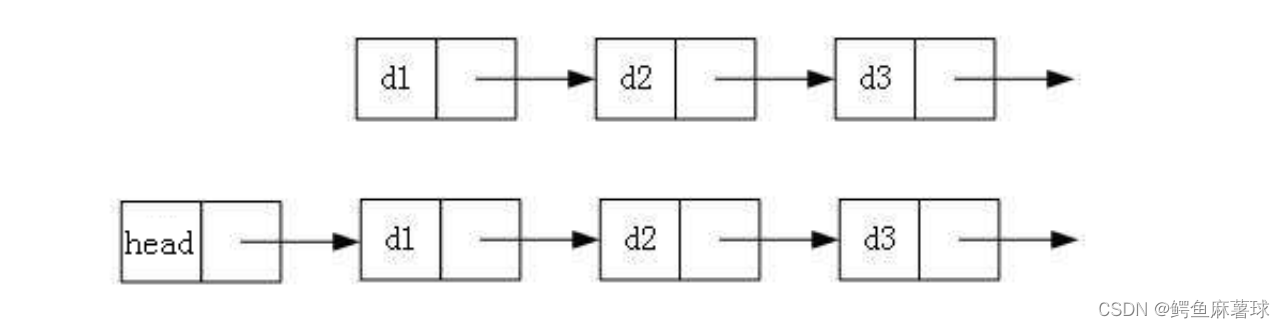
在这里插入图片描述

             

2.1创建空表

  我们定义了一个名为LinkList的类，代表一个单链表。这个类有两个私有成员：一个指向LNode类型的指针_head，代表链表的头节点，以及一个整型变量_size，代表链表的大小。

//定义单链表类
class LinkList
{
public:
	//默认构造函数
	LinkList()
	{
		_head = new LNode(0);//创建头结点(哨兵位节点)
		_size = 0;
	}
	
private:
	LNode* _head;
	int _size;
};

             

2.2头插法创建n个元素的线性链表

  先以头插单个元素为例：

  我们可以先创建一个新的节点来存储该元素。然后，检查链表是否为空，如果为空，则新节点就是链表的第一个节点； 否则，新节点将插入到当前头节点的后面。插入完成后，_size（代表链表元素个数的变量）加1。

void push_front(const int& val)
{
	//创建一个插入的新节点，将要插入的值val赋值给它
	LNode* newnode = new LNode(val);
	LNode* cur = _head->next;//保存原来第一个结点

	//进行头插操作
	_head->next = newnode;
	_head->next->next = cur;//连接原来的第一个节点

	_size++;
}

  加上n循环即可实现头插法创建n个元素的线性链表

//头插法创建n个元素
void push_front_n()
{
	cout << "请输入要插入的元素个数:";
	int n;
	cin >> n;
	cout << endl;
	cout << "输入要插入的元素:";
	while (n)
	{
		int tmp;
		cin >> tmp;
		push_front(tmp);
		n--;
	}
}

             

2.3一个带头节点的链表存放一组整数，设计一个算法删除值等于x的所有节点。

  无返回值版本

  我们先检查链表是否为空，如果为空，则输出一条错误消息并返回。如果链表非空，它开始遍历链表，检查每个节点的下一个节点是否为要删除的节点。如果是，则删除该节点并释放其内存；如果不是，则移动到下一个节点。 在遍历过程中，保持对当前节点的引用，以防止删除连续的要删除的节点时出现问题。

	//删除所有x的节点
void erase_all_x(int x)
{
	LNode* cur = _head;
	if (cur->next == nullptr)//判断是否为空链表
	{
		cout << "该链表为空不可删除\n";
		return;
	}
	else
	{
		while (cur && cur->next)//删除的数据有可能连续，所以最好保持当前节点
		{
			if (cur->next->data == x)//如果下一个节点为要删除节点
			{
				LNode* tmp = cur->next;//用临时指针保存要删除的节点
				cur->next = cur->next->next;//链表指向删除节点的下一个节点

				delete tmp;//删除节点中的元素
				tmp = nullptr;
			}
			else//如果下个节点不是删除节点，那直接指向下个节点
			{
				cur = cur->next;
			}
		}
	}
}

  有返回值版本

//删除所有x的节点，有删除节点返回true，无删除节点返回false
bool erase_all_x(int x)
{
	LNode* cur = _head;
	if (cur->next == nullptr)
	{
		cout << "该链表为空不可删除\n";
		return false;
	}
	else
	{
		int count = 0;//设计一个计数器，统计是否有删除的节点
		while (cur && cur->next)//删除的数据有可能连续，所以最好保持当前节点
		{
			if (cur->next->data == x)
			{
				count++;//有删除的节点，count++
				LNode* tmp = cur->next;
				cur->next = cur->next->next;//删除x节点

				delete tmp;
				tmp = nullptr;
			}
			else//如果下个节点不是删除节点，那直接指向下个节点
			{
				cur = cur->next;
			}
		}

		if (count == 0)//count==0，则没有可以删除的节点
		{
			cout << "链表中没有可以删除的元素" << endl;
			return false;
		}

		return true;
	}
}

             

2.4计算线性表中值为偶数的节点个数

  我们定义函数用于遍历链表并计算其中偶数节点的数量。首先，它检查链表是否为空，如果为空，则输出一条错误消息。如果链表非空，它开始遍历链表，检查每个节点的数据是否为偶数。如果是偶数，则计数器加1。 遍历完成后，输出链表中偶数节点的数量。

//打印链表中值为偶数的节点个数
void print_even_number()
{
	LNode* cur = _head->next;
	int count = 0;
	if (cur == nullptr)
	{
		cout << "该链表为空，没有节点\n";
	}
	else//核心就在不断通过指针遍历寻找即可
	{
		while (cur)//遍历链表中的每一个节点
		{
			if (cur->data % 2 == 0)
			{
				count++;//如果cur为偶数，计数++;
			}

			cur = cur->next;
		}

		cout << "该链表中偶数节点的个数为:" << count << endl;
	}
}

             

2.5一个带头节点的单链表heada存放一组整数，设计分裂heada算法，偶数放在heada中，奇数放在headb中

  我们定义该函数用于将链表中的偶数节点和奇数节点分开，使得偶数节点在heada链表中，奇数节点在headb链表中。

  函数使用两个指针cur1和cur2分别遍历heada和headb链表。在遍历过程中，如果当前节点的下一个节点是偶数节点，则保持原链表不变，移动cur1指针；

  如果当前节点的下一个节点是奇数节点，则将其从原链表中删除，并添加到headb链表的末尾，同时移动cur1和cur2指针。 最后，函数返回修改后的heada和headb链表。

//分裂链表，偶数在heada中，奇数在headb中
void divide_LinkList(LNode* heada, LNode* headb)
{
	LNode* cur1 = heada;
	LNode* cur2 = headb;

	while (cur1 && cur1->next)//退出循环的条件要cur1和cur1下个节点不为空
	{
		if (cur1->next->data % 2 == 0)//为偶数原链表不变
		{
			cur1 = cur1->next;//cur1直接向后移动
		}
		else//若链表为奇数，需要移动放入headb中
		{
			//交换链表节点操作
			LNode* tmp = cur1->next;
			cur1->next = cur1->next->next;
			
			//调整cur2，使其获得cur1的节点，断开cur1节点的后面节点的连接
			cur2->next = tmp;
			cur2->next->next = nullptr;

			//cur1和cur2各向后移动
			cur2 = cur2->next;
		}
	}
}

             

3.main函数和源码实现

3.1测试实现：

test_LinkList1();
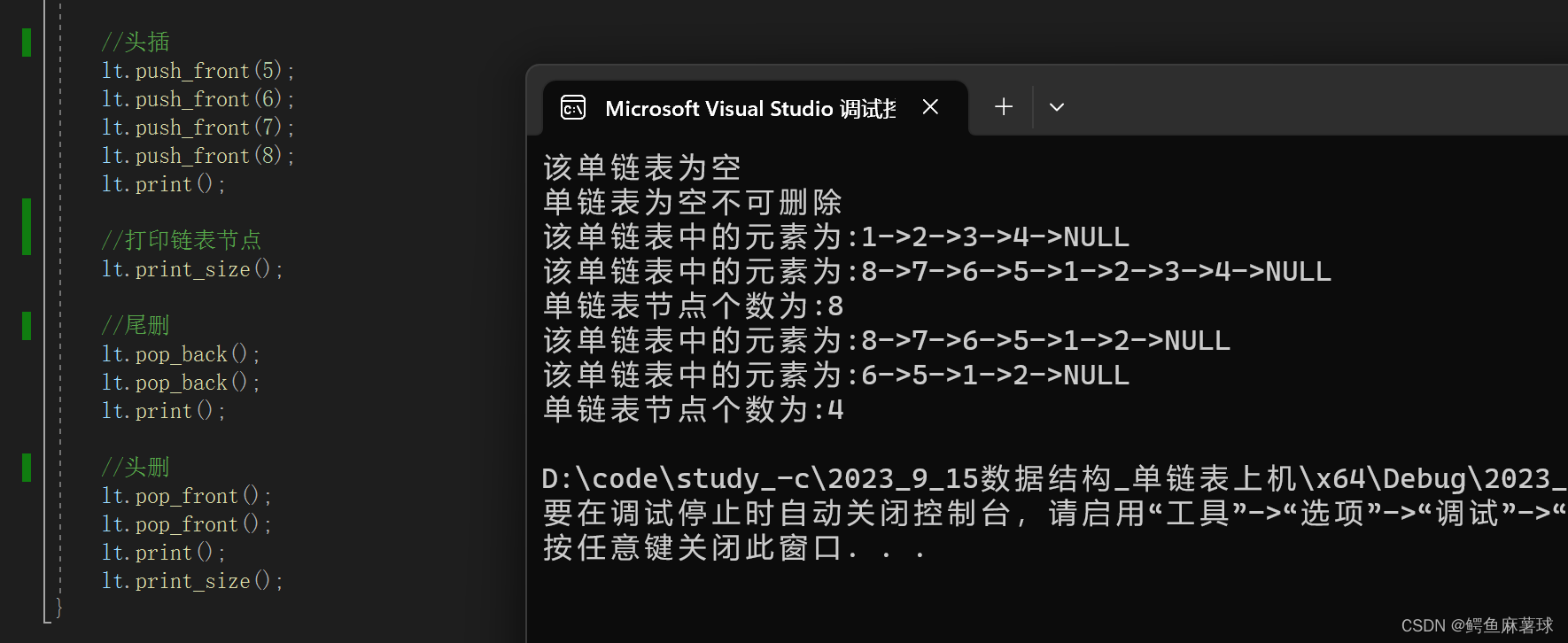
在这里插入图片描述

test_LinkList2();
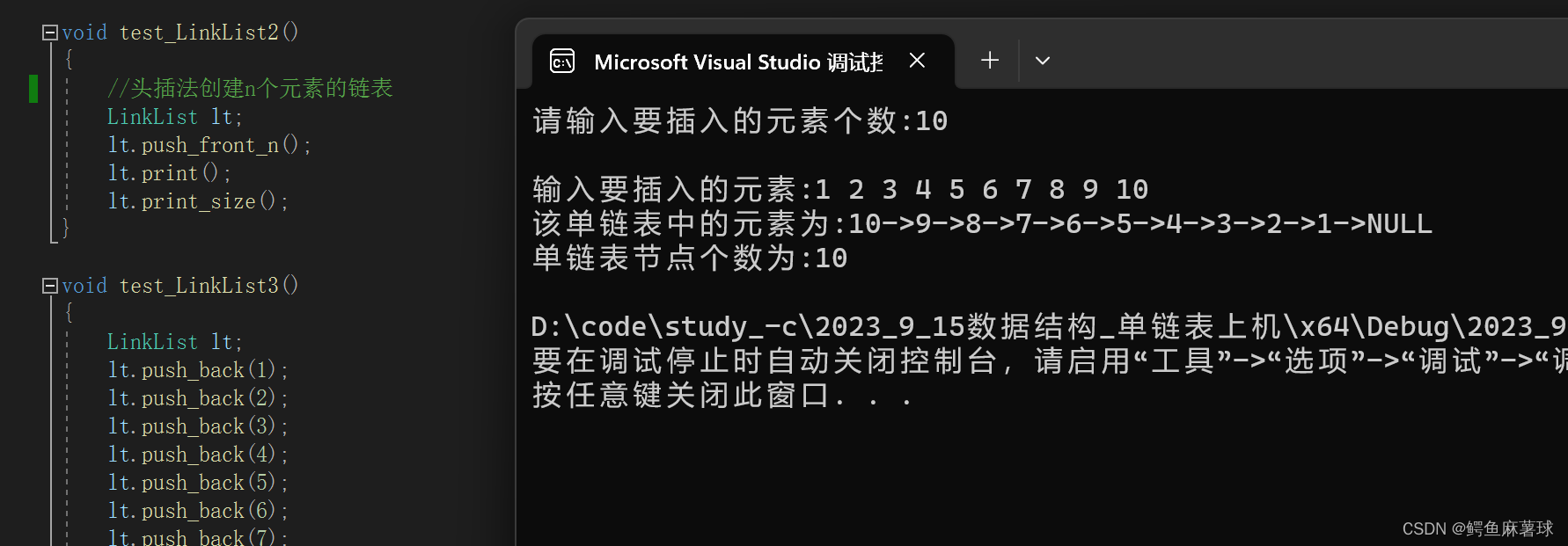
在这里插入图片描述

test_LinkList3();
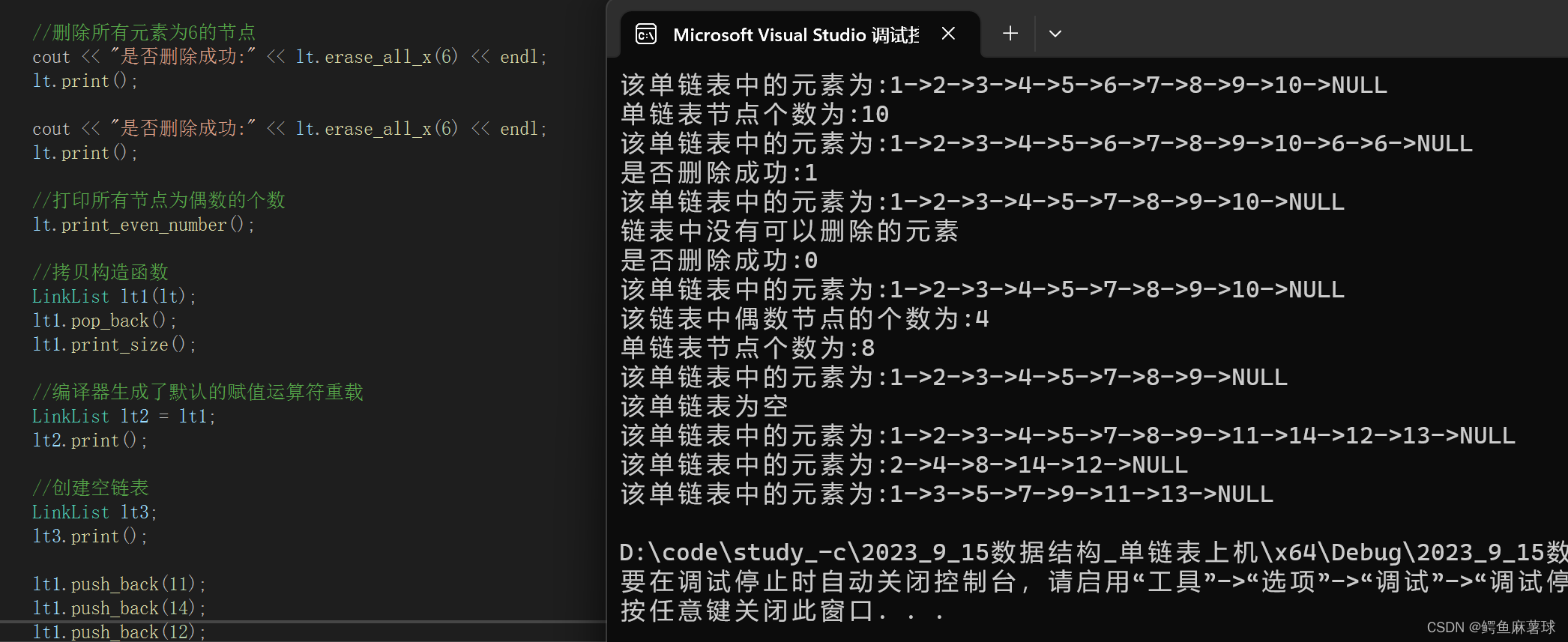
在这里插入图片描述

             

3.2LinkList.h

#pragma once

#include<assert.h>

//定义单链表节点
typedef struct LNode
{
	int data;
	LNode* next;

	LNode(const int& val)
		:data(val)
		, next(nullptr)
	{}

}LNode;

//定义单链表类
class LinkList
{
public:
	//默认构造函数
	LinkList()
	{
		_head = new LNode(0);//创建头结点(哨兵位节点)
		_size = 0;
	}

	//拷贝构造函数 lt1(lt)
	LinkList(const LinkList& lt)
	{
		LNode* oldcur = lt._head->next;

		//这个this指针是新建的链表lt1的
		this->_head = new LNode(0);
		this->_size = 0;

		LNode* newcur = _head;
		while (oldcur)//深拷贝以完成链表的赋值操作
		{
			//将旧链表中的值赋值到新链表中
			LNode* tmp = new LNode(oldcur->data);

			//向后移动新旧链表节点
			newcur->next = tmp;
			newcur = newcur->next;
			oldcur = oldcur->next;

			_size++;
		}
	}

	//析构函数
	~LinkList()
	{
		LNode* cur = _head->next;

		while (cur)
		{
			LNode* tmp = cur;
			cur = cur->next;

			delete tmp;
			tmp = nullptr;
		}
	}

	//单链表打印
	void print()
	{
		LNode* cur = _head->next;

		if (cur == nullptr)
		{
			cout << "该单链表为空\n";
		}
		else
		{
			cout << "该单链表中的元素为:";
			
			while (cur)
			{
				printf("%d->", cur->data);
				cur = cur->next;
			}

			cout << "NULL\n";
		}
	}

	//单链表尾插
	void push_back(const int& val)
	{
		LNode* newnode = new LNode(val);
		LNode* cur = _head;
		
		while (cur && cur->next)//找到尾结点
		{
			cur = cur->next;
		}

		cur->next = newnode;//尾插

		_size++;
	}

	//单链表头插
	void push_front(const int& val)
	{
		LNode* newnode = new LNode(val);
		LNode* cur = _head->next;

		_head->next = newnode;
		_head->next->next = cur;

		_size++;
	}

	//单链表尾删
	void pop_back()
	{
		LNode* cur = _head->next;
		LNode* prev = _head;

		if (cur == nullptr)
		{
			cout << "单链表为空不可删除\n";
		}
		else
		{
			while (cur && cur->next)//找到尾结点和前一个节点
			{
				cur = cur->next;
				prev = prev->next;
			}

			prev->next = nullptr;
			delete cur;
			cur = nullptr;
		
			_size--;
		}
	}

	//单链表头删
	void pop_front()
	{
		LNode* cur = _head->next;

		if (cur == nullptr)
		{
			cout << "单链表为空不可删除\n";
		}
		else
		{
			_head->next = cur->next;

			delete cur;
			cur = nullptr;
		
			_size--;
		}
	}

	//头插法创建n个元素
	void push_front_n()
	{
		cout << "请输入要插入的元素个数:";
		int n;
		cin >> n;
		cout << endl;
		cout << "输入要插入的元素:";
		while (n)
		{
			int tmp;
			cin >> tmp;
			push_front(tmp);
			//LNode* newnode = new LNode(tmp);
			//LNode* cur = _head->next;
			//if (cur == nullptr)
			//{
			//	_head->next = newnode;
			//}
			//else
			//{
			//	newnode->next = cur;
			//	_head->next = newnode;
			//}

			n--;
			//_size++;
		}
	}

	//删除第n个元素
	void erase(int n)
	{
		assert(n > 0 && n <= _size);

		LNode* cur = _head;
		if (cur->next == nullptr)
		{
			cout << "该链表为空不可删除\n";
			return;
		}
		else
		{
			LNode* tmp = cur;
			while (n)//找到删除节点的前一个位置
			{
				tmp = cur;
				cur = cur->next;
				n--;
			}

			tmp->next = tmp->next->next;
			delete cur;
			cur = nullptr;
		}
	}

	//单链表节点个数
	void print_size()
	{
		cout << "单链表节点个数为:" << _size << endl;
	}

	//删除所有x的节点，有删除节点返回true，无删除节点返回false
	bool erase_all_x(int x)
	{
		LNode* cur = _head;
		if (cur->next == nullptr)
		{
			cout << "该链表为空不可删除\n";
			return false;
		}
		else
		{
			int count = 0;//设计一个计数器，统计是否有删除的节点
			while (cur && cur->next)//删除的数据有可能连续，所以最好保持当前节点
			{
				if (cur->next->data == x)
				{
					count++;//有删除的节点，count++
					LNode* tmp = cur->next;
					cur->next = cur->next->next;//删除x节点

					delete tmp;
					tmp = nullptr;
				}
				else//如果下个节点不是删除节点，那直接指向下个节点
				{
					cur = cur->next;
				}
			}

			if (count == 0)//count==0，则没有可以删除的节点
			{
				cout << "链表中没有可以删除的元素" << endl;
				return false;
			}

			return true;
		}
	}

	//打印链表中值为偶数的节点个数
	void print_even_number()
	{
		LNode* cur = _head->next;
		int count = 0;
		if (cur == nullptr)
		{
			cout << "该链表为空，没有节点\n";
		}
		else
		{
			while (cur)//遍历链表中的每一个节点
			{
				if (cur->data % 2 == 0)
				{
					count++;//如果cur为偶数，计数++;
				}

				cur = cur->next;
			}

			cout << "该链表中偶数节点的个数为:" << count << endl;
		}
	}

	//返回当前链表的头结点
	LNode* get_head()
	{
		return _head;
	}

	//分裂链表，偶数在heada中，奇数在headb中
	void divide_LinkList(LNode* heada, LNode* headb)
	{
		LNode* cur1 = heada;
		LNode* cur2 = headb;

		while (cur1 && cur1->next)
		{
			if (cur1->next->data % 2 == 0)//为偶数原链表不变
			{
				cur1 = cur1->next;
			}
			else//若链表为奇数，需要移动放入headb中
			{
				//交换链表节点操作
				LNode* tmp = cur1->next;
				cur1->next = cur1->next->next;

				cur2->next = tmp;
				cur2->next->next = nullptr;

				//cur1和cur2各向后移动
				cur2 = cur2->next;
			}
		}
	}

private:
	LNode* _head;
	int _size;
};

             

3.3test.cpp

#define _CRT_SECURE_NO_WARNINGS 1

#include<iostream>
using namespace std;

#include"LinkList.h"

void test_LinkList1()
{
	LinkList lt;
	//链表打印
	lt.print();

	//测试空链表删除
	lt.pop_front();

	//尾插
	lt.push_back(1);
	lt.push_back(2);
	lt.push_back(3);
	lt.push_back(4);
	lt.print();

	//头插
	lt.push_front(5);
	lt.push_front(6);
	lt.push_front(7);
	lt.push_front(8);
	lt.print();
	
	//打印链表节点
	lt.print_size();

	//尾删
	lt.pop_back();
	lt.pop_back();
	lt.print();

	//头删
	lt.pop_front();
	lt.pop_front();
	lt.print();
	lt.print_size();
}

void test_LinkList2()
{
	//头插法创建n个元素的链表
	LinkList lt;
	lt.push_front_n();
	lt.print();
	lt.print_size();
}

void test_LinkList3()
{
	LinkList lt;
	lt.push_back(1);
	lt.push_back(2);
	lt.push_back(3);
	lt.push_back(4);
	lt.push_back(5);
	lt.push_back(6);
	lt.push_back(7);
	lt.push_back(8);
	lt.push_back(9);
	lt.push_back(10);
	lt.print();
	lt.print_size();

	lt.push_back(6);
	lt.push_back(6);
	lt.push_back(6);

	//删除第11节点的元素
	lt.erase(11);
	lt.print();

	//删除所有元素为6的节点
	cout << "是否删除成功:" << lt.erase_all_x(6) << endl;
	lt.print();

	cout << "是否删除成功:" << lt.erase_all_x(6) << endl;
	lt.print();

	//打印所有节点为偶数的个数
	lt.print_even_number();

	//拷贝构造函数
	LinkList lt1(lt);
	lt1.print();
	lt1.print_size();

	//编译器生成了默认的赋值运算符重载
	LinkList lt2 = lt1;
	lt2.print();

	//创建空链表
	LinkList lt3;
	lt3.print();

	lt1.push_back(11);
	lt1.push_back(14);
	lt1.push_back(12);
	lt1.push_back(13);
	lt1.print();

	//分离链表lt1，使lt1只含有偶数，lt3只含有奇数
	lt1.divide_LinkList(lt1.get_head(), lt3.get_head());
	lt1.print();
	lt3.print();
}

int main()
{
	//不想输入数据就调用test_LinkList1()或test_LinkList3();
	//test_LinkList1();
	//test_LinkList2();
	test_LinkList3();
	return 0;
}
更多推荐

计算机竞赛 深度学习+python+opencv实现动物识别 - 图像识别

文章目录0前言1课题背景2实现效果3卷积神经网络3.1卷积层3.2池化层3.3激活函数：3.4全连接层3.5使用tensorflow中keras模块实现卷积神经网络4inception_v3网络5最后0前言🔥优质竞赛项目系列，今天要分享的是🚩**基于深度学习的动物识别算法**该项目较为新颖，适合作为竞赛课题方向，学

Servlet

1Servlet1.1概念Servlet是JavaEE规范之一。规范就是接口Servlet是JavaWeb三大组件之一。三大组件分别是：Servlet程序、Filter过滤器、Listener监听器。Servlet服务于HTTP协议的服务端的一个小程序，“接收请求，解析请求，根据请求执行业务逻辑，做出响应”1.2实现功

【Spatial-Temporal Action Localization（七）】论文阅读2022年

文章目录1.TubeR:TubeletTransformerforVideoActionDetection摘要和结论引言：针对痛点和贡献模型框架TubeREncoder：TubeRDecoder：Task-SpecificHeads：2.HolisticInteractionTransformerNetworkforA

使用vue-cli搭建spa项目

目录一.什么是vue-cli二.安装vue-cli三.使用脚手架vue-cli(2.X版)来构建项目四.vue项目结构说明五.基于spa项目完成路由六.基于spa项目完成嵌套路由好啦！今天的分享就到这啦！！一.什么是vue-cliVueCLI是一个基于Vue.js的官方脚手架工具，用于快速启动、构建和管理Vue.js项

【论文阅读 05】图像异常检测研究现状综述

1图像异常检测任务图像异常检测任务根据异常的形态可以分为定性异常的分类和定量异常的定位两个类别.定性异常的分类：整体地给出是否异常的判断，无需准确定位异常的位置。如图2左上图所示,左侧代表正常图像,右侧代表异常图像,在第1行中,模型仅使用服饰数据集中衣服类型的样本进行训练，则其他类别的样本图像(鞋子等)对模型来说都是需

论文阅读 - Natural Language is All a Graph Needs

目录摘要IntroductionRelatedWork3InstructGLM3.1Preliminary3.2InstructionPromptDesign3.3节点分类的生成指令调整3.4辅助自监督链路预测4Experiments4.1ExperimentalSetup4.2MainResults4.2.1ogbn

机器学习—非零中心化、非零中心化会带来的问题

众所周知，激活函数最好具有关于零点对称的特性，不关于零点对称会导致收敛变慢。这种说法看到几次了，但对于背后的原因却一直比较模糊，今天就来捋一捋。神经元模型如图1所示是神经网络中一个典型的神经元设计，它完全仿照人类大脑中神经元之间传递数据的模式设计。大脑中，神经元通过若干树突（dendrite）的突触（synapse），

【数据结构练习】链表面试题集锦二

目录前言：1.链表分割2.相交链表3.环形链表4.环形链表II前言：数据结构想要学的好，刷题少不了，我们不仅要多刷题，还要刷好题！为此我开启了一个必做好题锦集的系列，每篇大约5题左右。此为第二篇选择题篇，该系列会不定期更新敬请期待！1.链表分割代码：publicclassPartition{publicListNode

Hadoop-sqoop

sqoop1.Sqoop简介及原理简介：Sqoop是一款开源的工具,主要用于在Hadoop(Hive)与传统的数据库(mysq1.postgresql..)间进行数据的传递，可以将一个关系型数据库（例如:MySQL,Oracle,Postgres等）中的数据导进到Hadoop的HDFS中，也可以将HDFS的数据导进到关

JVM基础知识(内存区域划分,类加载,GC垃圾回收)

目录内存区域划分JVM中的栈JVM中的堆程序计数器方法区(元数据区)给一段代码,某个变量在哪个区域上?类加载类加载时机双亲委派模型GC垃圾回收机制GC实际工作过程1.找到垃圾/判定垃圾1.可达性分析(Java中的做法)2.引用计数2.清理垃圾1.标记清除2.复制算法3.标记整理分代回收(复制算法+标记整理)内存区域划分

Axios 的介绍（使用和作用）

Axios是一个基于promise的HTTP库，可以用在浏览器和node.js中axios的作用是什么呢？axios主要是用于向后台发起请求的，还有在请求中做更多是可控功能。axios特点：从浏览器中创建XMLHttpRequests从node.js创建http请求支持PromiseAPI拦截请求和响应（就是有inte

热文推荐
  1. 二叉树的概念、存储及遍历

    一、二叉树的概念1、二叉树的定义二叉树（binarytree）是n个结点的有限集合，该集合或为空集（空二叉树），或由一个根结点与两棵互不相交的，称为根结点的左子树、右子树的二叉树构成。二叉树的特点是：（1）每个结点最多有两棵子树，故二叉树中不存在度大于2的结点。（2）二叉树是有序的，其次序不能任意颠倒，即使树中的某个结

  2. 利用Socks5代理IP加强跨界电商爬虫的网络安全

    随着跨界电商的兴起，爬虫技术在这个领域变得越来越重要。然而，网络安全一直是一个值得关注的问题。在本文中，我们将讨论如何利用代理IP和Socks5代理来增强跨界电商爬虫的网络安全，确保稳定和可靠的数据采集，同时避免封禁和风险。背景跨界电商是一个竞争激烈的领域，市场上的商品信息和价格常常会变动。为了保持竞争力，电商企业需要

  3. CFGPT: Chinese Financial Assistant with Large Language Model

    本文是LLM系列文章，针对《CFGPT:ChineseFinancialAssistantwithLargeLanguageModel》的翻译。CFGPT：大型语言模型的中文财务助理摘要1引言2相关工作3数据集4模型和训练5应用6结论摘要大型语言模型（LLM）在金融领域的自然语言处理任务中显示出巨大的潜力。在这项工作中

  4. 医疗虚拟仿真和虚拟现实有什么区别？哪个更好？

    随着我们在仿真教育中越来越多地使用新技术，区分虚拟模式的类型很重要。虚拟仿真是一个统称，用来概括术语来描述各种基于仿真的体验，从基于屏幕的平台到沉浸式虚拟现实。然而，各虚拟平台在保真度、沉浸感和临场感的水平上有很大差异。医疗教育中存在许多虚拟解决方案的空间，对于护理虚拟仿真课程来说，没有"一刀切"的模式。在此就给大家介

  5. 如何完美通过token获取用户信息（springboot）

    1.什么是Token？身份验证令牌（AuthenticationToken）：在身份验证过程中，“token”可以表示一个包含用户身份信息的令牌。例如Token（JWT）是一种常见的身份验证令牌，它包含用户的身份信息（例如用户名或用户ID）以及其他相关信息，如权限或过期时间。无意义令牌token，这种一般在获取后通过n

  6. 芯片SoC设计你了解吗？

    数字IC设计根据岗位性质一般包含SOC设计，前端设计，ASIC设计，逻辑设计，IP设计，CPU设计等。有人说：做IP设计就是翻译官，做SOC设计就是连连看。SoC设计是做什么的？与IP设计有什么不同？IP设计工程师每天的工作，编码，debug，接口定好了，时钟只给一个，内部不让分频。不用做过异步处理。按照公司的编码规范

  7. js实现短信验证码一键登录

    前言短信验证码一键登录是一种方便快捷的登录方式，用户只需输入手机号码，然后接收到手机短信验证码并自动填入验证码框，即可完成登录操作。本文将介绍短信验证码一键登录的原理，并给出一个简单的示例说明。短信验证码一键登录的原理用户输入手机号码：用户在登录界面输入手机号码，并点击获取验证码按钮。发送验证码：前端通过API向后端发

  8. Linux--线程（与进程区别）

    Linux线程1、线程与进程进程可以看成只有一个控制线程：一个进程同时只做一件事情。有了多个控制线程后，可以把进程设计成在同一时刻做不止一件事，每个线程各自处理独立的任务。进程是程序执行时的一个实例，是分配系统资源（CPU时间、内存等）的基本单位。进程本身不是基本运行单位，而是线程的容器。一个进程可以拥有多个线程。进程

  9. 【智能家居-大模型】行业专题报告：ChatGPT等大模型催化智能家居行业发展

    （报告出品方/作者：华安证券，马远方）1智能家居：ChatGPT等大模型为行业发展带来新机遇1.1现状：智能家居产品的用户体验（交互能力、智能化水平）及安全性待提升智能家居：智能化的家庭系统，增加生活便利、舒适、安全。智能家居是指通过互联网技术和智能设备，将家庭设备、家庭电器、家庭安全等各种家居设施连接，实现智能控制、