2.1 无符号数和有符号数
2.1.1 无符号数
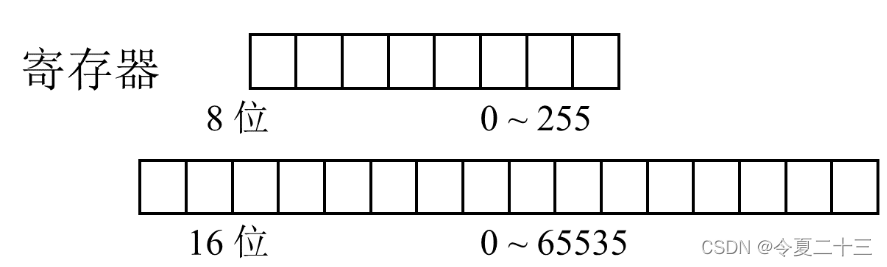
没有符号的数,其实就是非负数。在计算机中用字节码表示,目前最常用的是八位和十六位的。
2.1.2 有符号数
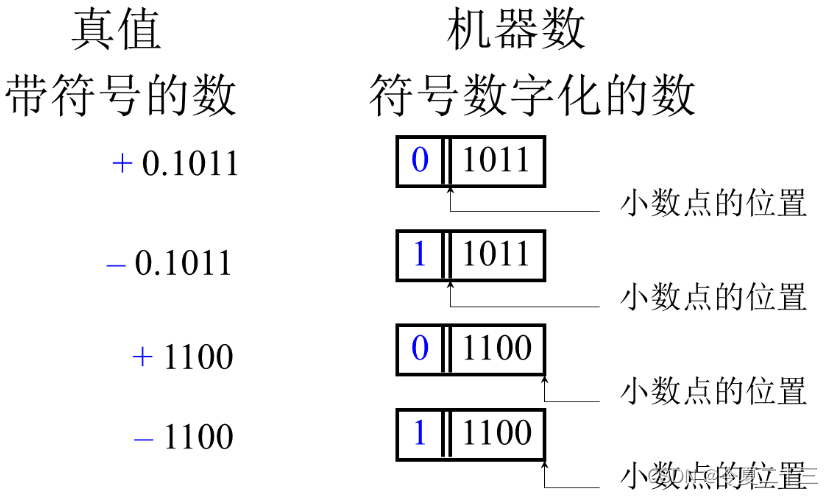
将正负符号数字化,0代表 + ,1代表 - ,并把代表符号的数字放在有效数字前,就组成了有符号数。
1. 机器数和真值
我们接下来要用到的真值都指的是带符号的二进制数。
机器数是相对于真值而言的,下面要讲的原码、补码、反码和移码都属于机器数。
2. 原码表示法
原码,顾名思义,是机器数最原本的表示方法,原码包括两个部分,符号位和数值位,符号位用0和1代表这个数的正负,数值位就是真值的绝对值。
为了区别用原码表示的整数和小数,整数的符号位和数值位用逗号隔开,小数的则用小数点隔开。
原码的优点:表示简单,易于和真值转换。
原码的定义 -- 整数

原码的定义 -- 小数
原码可以表示的小数范围在-1和1之间,其他带小数的数可以用整数+小数这样的组合来表示。

例题
注意,在由原码求真值的题目中,若结果为正,那也得加一个 + 号!


3. 补码表示法
补的概念
取模为12的时候,+2等价于-10,-4等价于+8,+3等价于+15等价于+27。
在上面的例子里,-10的补数为+2,-4的补数为+8。并且正数的补数是其本身。
由此可以知道,只要确定了模,就可以为任何一个负数找到与其对应的正数,也就是补数,这样就方便进行运算,在对含有负数的式子进行加法运算时,可以先将负数取补数,最后取模即可。
补的结论

补码的定义 -- 整数
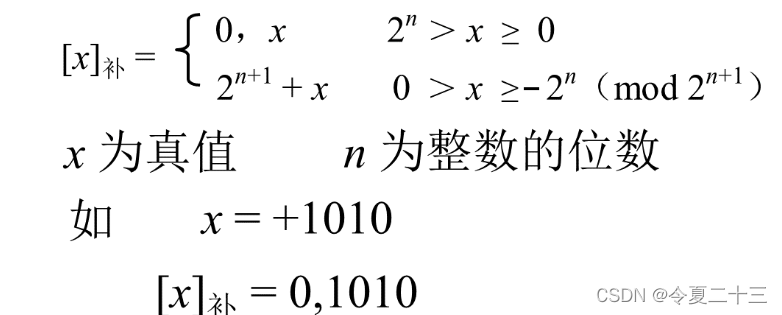
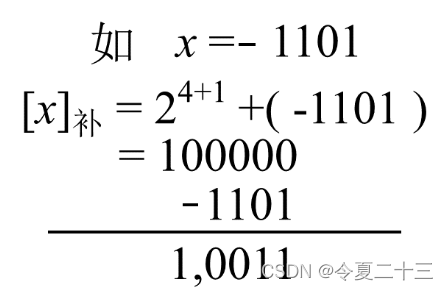
补码的定义 -- 小数
用补码表示负的小数时,因为符号位要为1,所以应该模2,也就是用2减去真值,这样得到的结果里,符号位一定为1,数值位即为真值的补数。
要注意,2也得用二进制来表示!
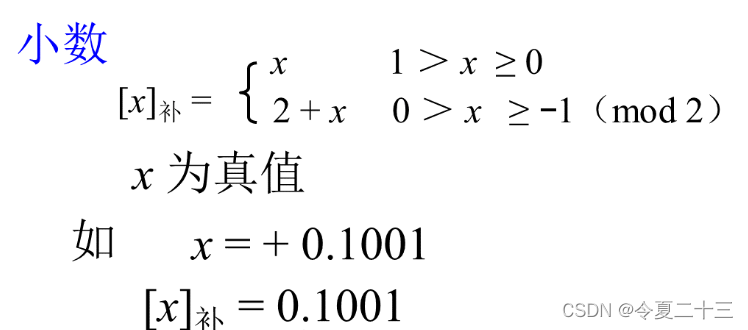

变形补码 -- 双符号位补码



求补码的快捷方式
对正数来说,补码就是符号位加上真值本身,简单易求;
对负数来说,求补码则有快捷方式:

总而言之,就是符号位不变,数值位取反,末尾加一。
4. 反码表示法
反码通常是基于上面原码与补码转换的快捷方式,所需要的中间过渡。
由于正数不需要快捷方式,所以反码还是和原码补码一样,只有符号位和真值不同。
只有负数需要将全体数值位转换为相反的数。
反码的定义 -- 整数

反码的定义 -- 小数
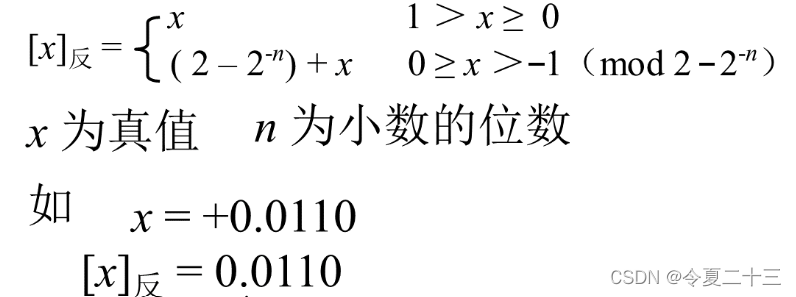

例题


5. 移码表示法
用原码和补码时很难一眼比出两个数的大小,这时候就需要使用移码了。
移码的定义

移码的特点

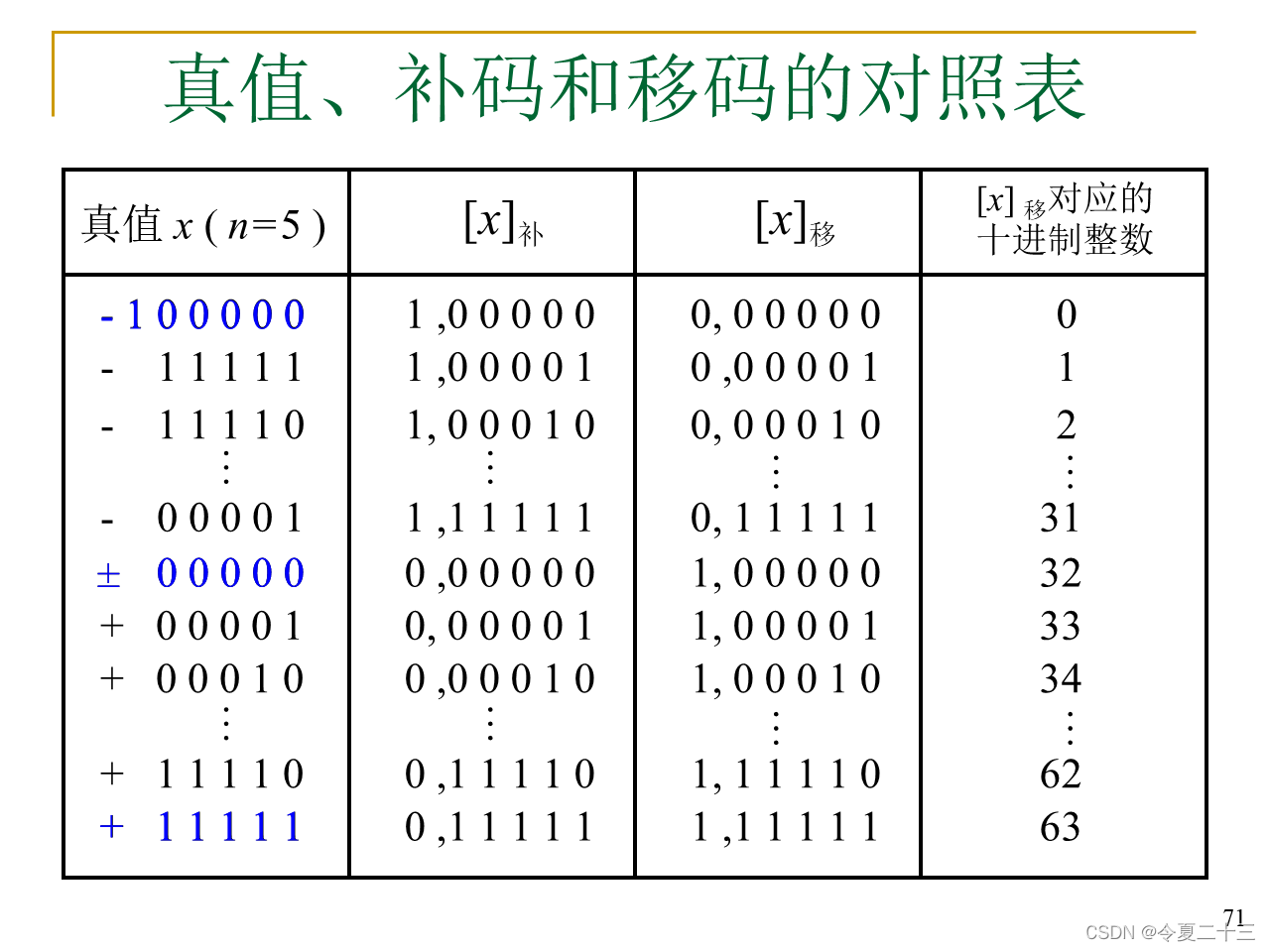
同一个真值的移码和补码只差一个符号位。
作业题知识点补充
1. 分数转换为二进制数
以 29/128 为例:
第一步
把分子和分母都转换为二进制,要表示为2的多少次。
那么分子表示为:2^4+2^3+2^2+2^0
那么分母呢:2^7
继续将他们写成分数形式:(2^4+2^3+2^2+2^0)/2^7。
接下来计算就好了,结果为:2^-3+2^-4+2^-5+2^-7。
第二步
讲一个小知识点:对于二进制数左移是放大2倍,右移是缩小2倍。
那么对于二进制1,我们右移得到0.1,缩小2倍。所以0.1代表1/2,即2-1。同理,0.01就是1/4,即2-2,以此类推。
有了这个基础,再看看上面的式子,不就是0.001+0.0001+0.000 01+0.000 0001。
用二进制加法计算出最后结果,即0.001 1101。
2. 无原码的特殊情况
补码为1.0000的真值为-1,但是没有原码,因为小数原码的范围如下:
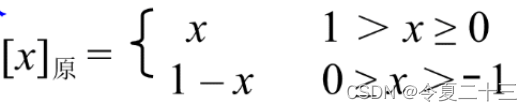
可知,小数1和-1都没有原码。
补码为1,0000的真值为-16,但也没有原码,因为整数原码的范围如下:
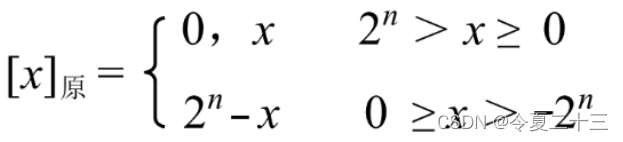
当数值位有四位时,原码的取值只能小于+16。
3. 十六进制转换为二进制
每个十六进制数都代表四位二进制数,所以直接按位置转换即可。
0 ~ 9 都可以当成十进制数化为二进制数,只是不足的要补足至四位,而剩下的则如下表所示:
| 十六进制 | 十进制 | 二进制 |
| A | 10 | 1010 |
| B | 11 | 1011 |
| C | 12 | 1100 |
| D | 13 | 1101 |
| E | 14 | 1110 |
| F | 15 | 1111 |
2.2 数的定点表示和浮点表示
2.1.1 定点表示

2.1.2 浮点表示

规格化数:浮点数的尾数以1开头,例如0.110101。
1. 浮点数的表示形式
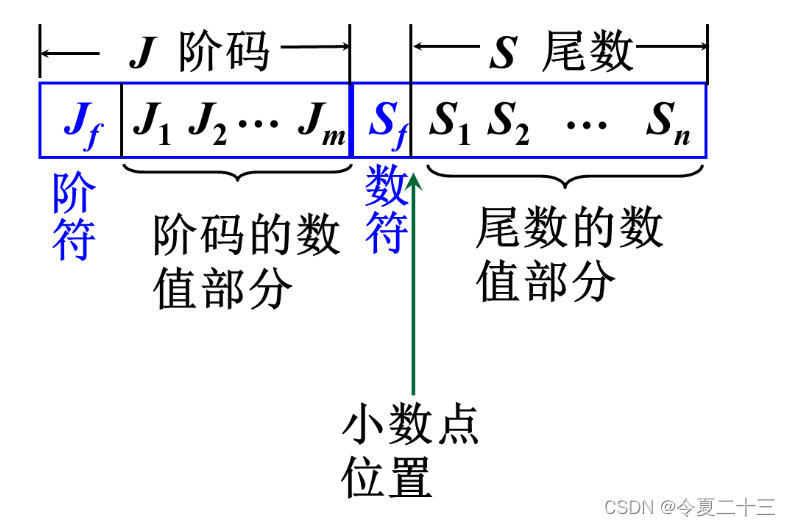

2. 浮点数的表示范围

3. 浮点数的规范化

2.2.3 定点数和浮点数的比较
- 当浮点机与定点机中的数其位数相同时,浮点数的表示范围比定点数大得多。(浮点机和定点记中的数都表示为机器数)
- 当浮点数为规格化数时,其精度远高于定点数。
- 浮点数运算分阶码和尾数部分,而且运算结果要求规格化。
- 在溢出的判断方法上,浮点数是对规格化的阶码进行判断,而定点数是对数值本身进行判断。





