def listSum(numbers):
    if not numbers:
        return 0
    else:
        (f, rest) = numbers
    return f + listSum(rest)

myList = (1, (2, (3, (4,None))))
total = listSum(myList)
print(total)

while循环何时退出？ 恐怕是while循环技巧所在，即选择恰当的变量作为退出循环的条件判断。

下面的栗子选择了哪个变量作为退出条件？

原题来自宁波第23届中小学信息比赛小学组决赛最后一道题。尝试用python代替原题要求的pascal count.pas/exe）

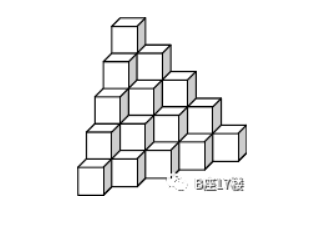
问题描述： 小Q的编程技术在一次搭积木比赛中也成了秘密武器。原来，比赛的规则是这样的：给你N个小木块（全部为一样大小的正方体）。快速搭成如下图规则的形状（下图为5层的规模），要求层数为最大限度。

由于小Q编了个程序，只要输入小木块的个数N，就可以马上求出最多可以搭几层，还剩几个，所以小Q每次都是一次成功，从不需要翻工，速度也就领先了，你会编小Q这样的程序吗？

【输入数据】

输入文件count.in：文件中只有一个整数N，表示小木块的个数，已知1≤N≤2^31。

【输出数据】

输出文件count.out：文件中有两行整数，第一行是最多可以堆的层数，第二行是剩余的小木块

Python语言的搭积木的诀窍 解法仅供参考

图片

递归的妙处：

第一条：每次递归都能将问题规模缩减下来。

第二条：对应递归终止条件，递归必须有个出口，不然会陷入无限递归当中。

第三条：将递归问题细分为更小的递归问题，然后再进行递归调用。

首先，只需要找到相邻两层之间数量关系，较大层数和小木块数量之间的关系表达为为consumer()函数

请看图：第1层是1，第2层是3，第3层用掉的木块是x，那么前3层用掉的木块总数是前2层用掉的总数，再加上第3层的木块数量。

留意：前3层和第3层所指不同，显然前3层包含第3层。持续倒推，就可以建立起第n层和第1层之间的数量关系。

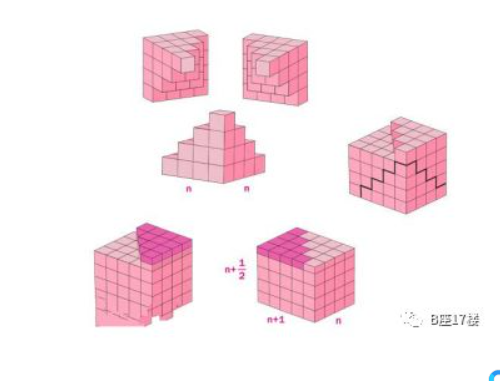
第n-1层需要多少个小木块作为输入参数，

x = consumer(n-1)

推出第n层需要多少小木块,

consumer(n)=consumer(n-1) + 0.5*(n**2+n)

为啥是第2层开始，总能表达为

consumer(n-1) + 0.5*(n**2+n)

为何1-> n 层的cube总的数量 = 第 n-1 层数量 + 0.5*(n**2+n)

符合以上数学关系的理由是第 n 层木块数量与 n 存在关系，不妨从求解三角形的面积公式得到灵感：

1+2+3+....n = 0.5*(n**2+n)

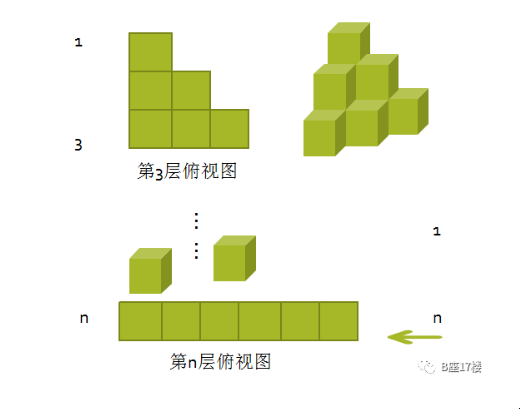
第n层的平面图计算高斯数

please enter the cube numeber:20
4， 0

please enter the cube numeber:100
7， 16.0

please enter the cube numeber:1000
17， 31.0

但python递归的问题爆栈在随手将 n 大到离谱时如约而至！呵呵

please enter the cube numeber:10000000000000

...
RecursionError: maximum recursion depth exceeded in comparison

那么，这时候有两个办法：

1、设法取消递归栈的上限：996 次； 2、或者改用循环的递推实现；

如何理解递归和循环？

SOLID原则：

分离出子函数layerSum(n)计算第 n 层有多少cube;

主函数 consumeWhile(total)判断累积cube超过total为退出循环的条件判断；

*可以与递归写法的结果比较是否一致

# SOLID分离原则 
def layersSum(n):
    # 第 n 层有多少cube
    return 0.5 *(n**2 + n)

上述可以灵活修改每一层的几何形状，如改为正方形等等；

def consumeWhile(total):
    # 表达相邻两层之间的数量关系
    # cur,upper = layers(1),layers(2)
    # upper变量是从 1-n 层共有多少cube
    cur,layer = 0,0
    while cur <= total:
        cur += layersSum(layer)
        if cur == total:
            return layer,0
        elif cur > total:
            return layer-1,total - (cur-layersSum(layer))
        layer += 1
        
        
total = 100000000
print(consumeWhile(total))

(842, 153956.0)

递归的写法优雅而有趣，但实际项目工程中并不是首选。正如在while循环中看到当 total 数字很大时，递归的不仅运算花费的时间多且易溢出而报错。

这时循环的写法系统的开销更少。