文章目录

一、二叉树的遍历
后文所有代码中的二叉树结点:
typedef char BTDataType;
//二叉树结点结构体
typedef struct BinaryTreeNode
{
BTDataType data;
struct BinaryTreeNode* left;
struct BinaryTreeNode* right;
}BTNode;
1、前序遍历
前,中,后序遍历都可以采用分治递归的思想解决,将根节点和它的孩子结点分别处理。
// 二叉树前序遍历
void BinaryTreePrevOrder(BTNode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
printf("%c ", root->data);
BinaryTreePrevOrder(root->left);
BinaryTreePrevOrder(root->right);
}
此处仅利用递归展开图分析前序遍历,中序和后序也是相同的思想:
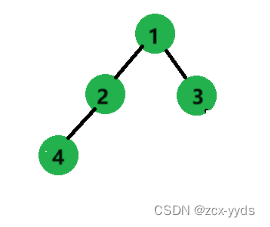

2、中序遍历
// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
BinaryTreeInOrder(root->left);
printf("%c ", root->data);
BinaryTreeInOrder(root->right);
}
3、后序遍历
// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
BinaryTreePostOrder(root->left);
BinaryTreePostOrder(root->right);
printf("%c ", root->data);
}
4、层序遍历
层序遍历需要利用队列来进行,如果二叉树跟结点不为空,则让指向它的一个指针入队,然后将队头结点记录下来,先将它的值打印,然后判断它的左右孩子为非空则入队,然后删掉队头换下一个继续记录打印…直到队列为空则遍历完成。
例如对如图这个二叉树:
层序遍历结果为:12345
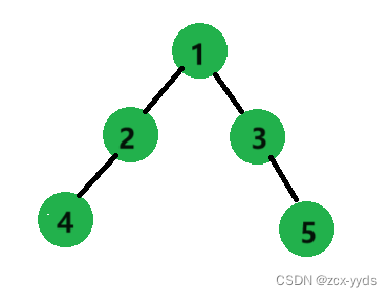
先将根节点1入队,打印1
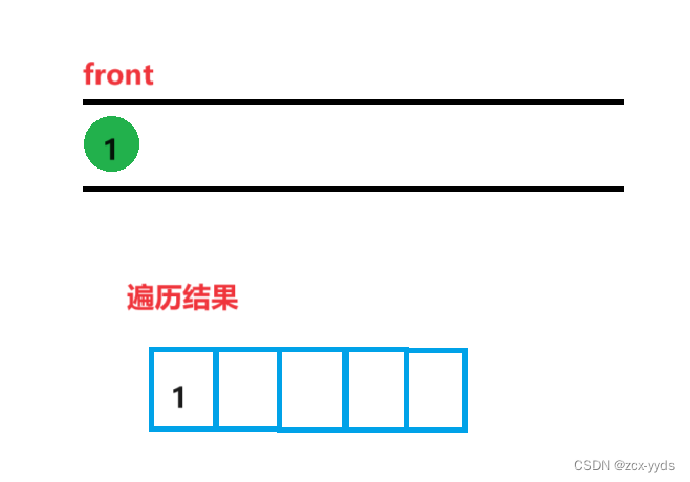
然后将1的左右孩子2和3入队
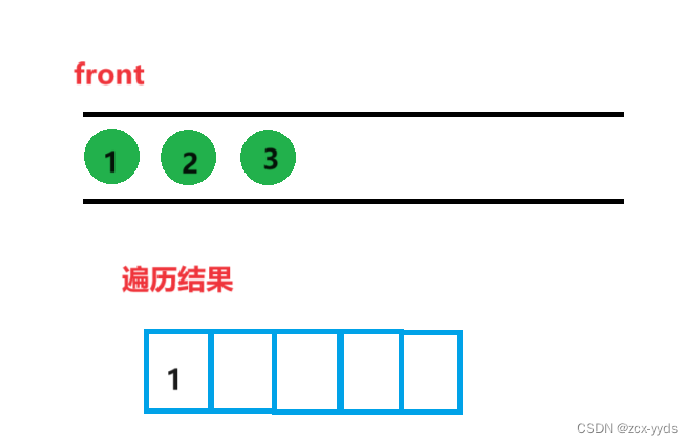
删掉队头1,front换为2,打印2

然后将2的左孩子4入队
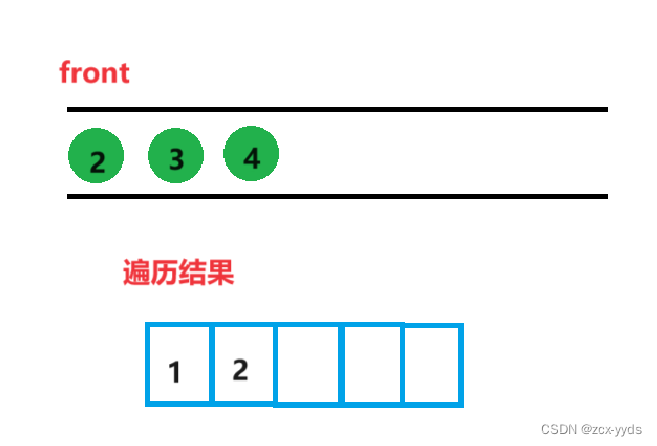
删掉队头2,front换为3,打印3
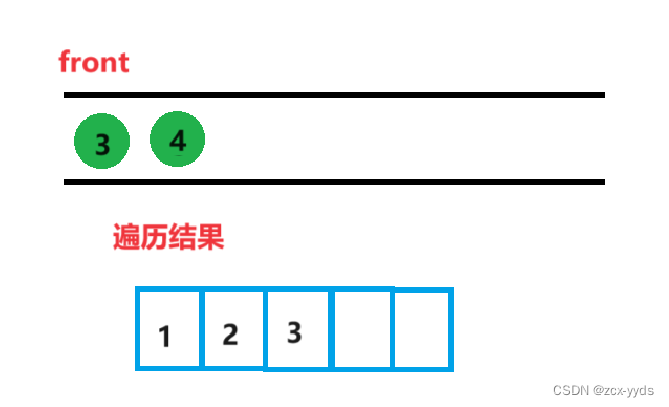
然后将3的右孩子5入队
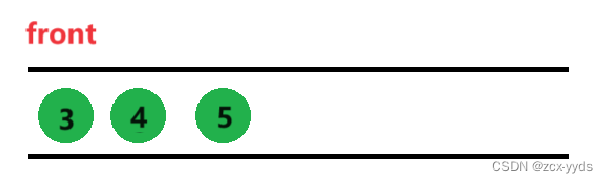
… …
接着按这样打印4,5便完成了二叉树的层序遍历
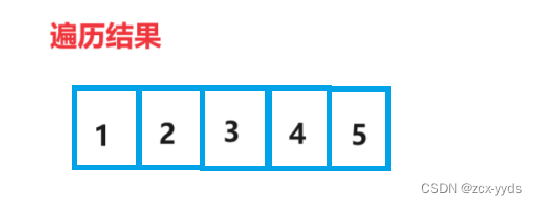
程序代码利用了自己创建的队列,代码如下:
//层序遍历
void LevelOrder(BTNode* root)
{
//创建队列
Que q;
QueueInit(&q);
//如果根节点不为空,则放进队列
if (root)
QueuePush(&q, root);
while (!QueueEmpty(&q))
{
//将队头打印
BTNode* front = QueueFront(&q);
printf("%c ", front->data);
//判断front左右节点不为空则入队
if (front->left)
QueuePush(&q, front->left);
if (front->right)
QueuePush(&q, front->right);
QueuePop(&q);
}
printf("\n");
QueueDestroy(&q);
}
二、二叉树结点个数及高度
1、二叉树节点个数
采用分治法递归实现,当根节点为空时返回值为0,不为空则返回左右子树上的节点数加上自身1。
int BinaryTreeSize(BTNode* root)
{
return root == NULL ? 0 : BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;
}
2、二叉树叶子节点个数
采用分治法递归实现,根节点为空时返回0,当根节点没有孩子结点时说明它是叶子节点,返回1,其他情况时只需左右子树上的叶子节点相加即可。
int BinaryTreeLeafSize(BTNode* root)
{
if (root == NULL)
{
return 0;
}
if (root->left == NULL && root->right == NULL)
{
return 1;
}
return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}
3、二叉树第k层节点个数
需要保证k大于0才可,当根节点为空,则返回0,当k等于1时只有一层一个节点,返回1,k>1时第k层节点数就相当于它左右孩子的第k-1层节点数相加。
int BinaryTreeLevelKSize(BTNode* root, int k)
{
assert(k > 0);
if (root == NULL)
{
return 0;
}
if (k == 1)
{
return 1;
}
return BinaryTreeLevelKSize(root->left, k - 1)
+ BinaryTreeLevelKSize(root->right, k - 1);
}
4、二叉树查找值为x的节点
跟节点为空则找不到返回NULL,当根节点的值为要找的值时返回该节点,不相等则分别判断它的左右孩子节点,直到找到为止。
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
if (root == NULL)
{
return NULL;
}
if (root->data == x)
{
return root;
}
BTNode* ret = BinaryTreeFind(root->left,x);
if (ret)
{
return ret;
}
return BinaryTreeFind(root->right, x);
}
三、二叉树创建及销毁
1、通过前序遍历数组创建二叉树
读入用户输入的一串先序遍历字符串,根据此字符串建立一个二叉树(以指针方式存储)。 例如如下的先序遍历字符串: ABC##DE#G##F### 其中“#”表示的是空格,空格字符代表空树。建立起此二叉树以后,再对二叉树进行中序遍历,输出遍历结果。
#include <stdio.h>
#include<stdlib.h>
typedef char BTDataType;
typedef struct BinaryTreeNode {
BTDataType data;
struct BinaryTreeNode* left;
struct BinaryTreeNode* right;
} BTNode;
BTNode* BinaryTreeCreate(BTDataType* a, int* pi) {
if (a[*pi] == '#') {
++*pi;
return NULL;
}
BTNode* root = (BTNode*)malloc(sizeof(BTDataType));
root->data = a[*pi];
++*pi;
root->left = BinaryTreeCreate(a, pi);
root->right = BinaryTreeCreate(a, pi);
return root;
}
//中序遍历
void InOrder(BTNode* root)
{
if(root==NULL)
{
return;
}
InOrder(root->left);
printf("%c ",root->data);
InOrder(root->right);
}
int main() {
char a[100];
scanf("%s",a);
int pi=0;
BTNode* root=BinaryTreeCreate(a, &pi);
InOrder(root);
return 0;
}
2、二叉树的销毁
void BinaryTreeDestory(BTNode* root)
{
if (root == NULL)
{
return;
}
BinaryTreeDestory(root->left);
BinaryTreeDestory(root->right);
free(root);
}
3、判断是否为完全二叉树
在二叉树层序遍历的基础上修改一下,让空节点也进入队列,遍历时遇到空节点则退出,继续遍历如果结束前还有非空节点则不是完全二叉树。
int BinaryTreeComplete(BTNode* root)
{
//创建队列
Que q;
QueueInit(&q);
//如果根节点不为空,则放进队列
if (root)
QueuePush(&q, root);
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
if (front == NULL)
{
break;
}
QueuePush(&q, front->left);
QueuePush(&q, front->right);
QueuePop(&q);
}
//此时已经遇到空节点,如果再遇到非空节点则不是完全二叉树
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
if (front)
{
QueueDestroy(&q);
return false;
}
QueuePop(&q);
}
QueueDestroy(&q);
return true;
}
四、测试代码
手动构建一个如下图的二叉树,对代码进行测试:
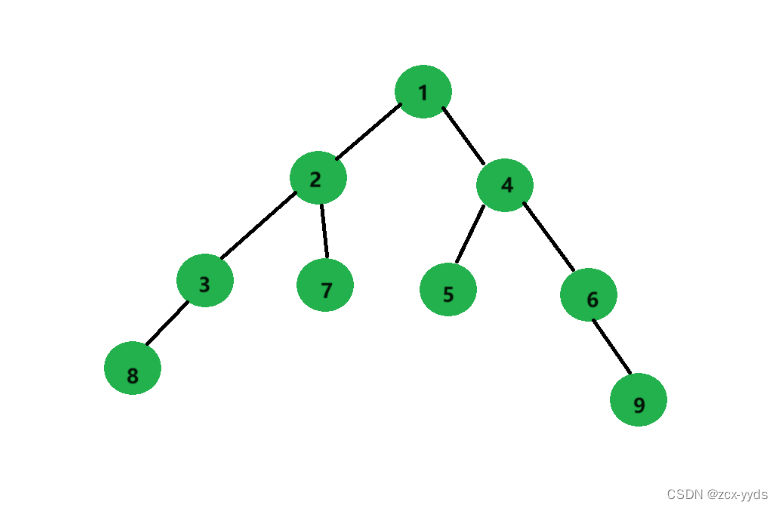
测试结果应该为:
前序:123874569
中序:832715469
后序:837259641
是否为完全二叉树:0
节点数:9
叶子节点数:4
BTNode* BuyNode(BTDataType x)
{
BTNode* node = (BTNode*)malloc(sizeof(BTNode));
if (node == NULL)
{
perror("malloc fail");
exit(-1);
}
node->data = x;
node->left = NULL;
node->right = NULL;
return node;
}
int main()
{
// 手动构建
BTNode* node1 = BuyNode('1');
BTNode* node2 = BuyNode('2');
BTNode* node3 = BuyNode('3');
BTNode* node4 = BuyNode('4');
BTNode* node5 = BuyNode('5');
BTNode* node6 = BuyNode('6');
BTNode* node7 = BuyNode('7');
BTNode* node8 = BuyNode('8');
BTNode* node9 = BuyNode('9');
node1->left = node2;
node1->right = node4;
node2->left = node3;
node4->left = node5;
node4->right = node6;
node2->right = node7;
node3->left = node8;
node6->right = node9;
printf("前序遍历:");
BinaryTreePrevOrder(node1);
printf("\n");
printf("中序遍历:");
BinaryTreeInOrder(node1);
printf("\n");
printf("后序遍历:");
BinaryTreePostOrder(node1);
printf("\n");
printf("层序遍历:");
LevelOrder(node1);
printf("\n");
printf("BinaryTreeComplete:%d\n", BinaryTreeComplete(node1));
printf("BinaryTreeSize:%d\n", BinaryTreeSize(node1));
printf("BinaryTreeLeafSize:%d\n", BinaryTreeLeafSize(node1));
BinaryTreeDestory(node1);
node1 = NULL;
return 0;
}
运行结果:
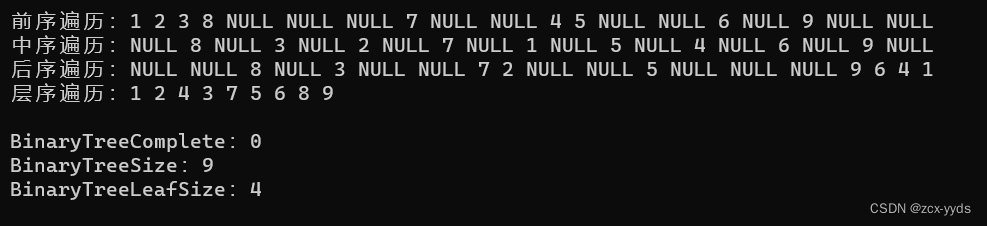
运行结果与预测结果一致。







