• 线性扫描是一种最简单的计算机文档检索方式，这个过程通常称为grepping。在使用现代计算机的条件下，对一个规模不大的文档集进行线性扫描非常简单，根本不需要做额外的处理。
• 但在（1）大规模文档集（2）更灵活的匹配方式（3）需要对结果进行排序的情况下，就不能再用上边的线性扫描。一种非线性扫描的方式是事先给文档建立索引（index）。

📚词项-文档关联矩阵

🐇相关名词

• 词项（Term）：索引的单位，通常用词来表示。
• 文档（Document）：检索系统的检索对象，可以是单独的一条记录或者是一本书的各章。
• 文档集/语料库（collection/corpus）：所有文档的集合。
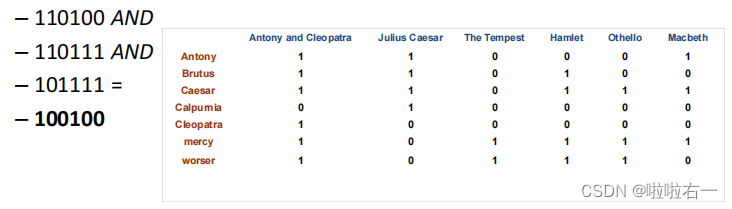
• 词项-文档关联矩阵（Term-document incidence matrices）
  

• 从行看，可以得到每个词项对应的文档向量，表示词项在哪些文档出现或不出现。
• 从列看，可以得到每个文档对应的词项向量，表示文档中哪些词项出现或不出现。

🐇词项-文档关联矩阵的布尔查询处理

• 对于采用AND、OR及NOT等逻辑操作符连接起来的布尔表达式查询，通过对文档向量间接逻辑操作来得到查询结果。
• 例：响应查询Brutus AND Caesar AND NOT Calpurnia：结果向量中的第1和第4个元素为1，这表明该查询对应的剧本是Antony and Cleo patra和Hamlet。
  
• 假设有50万个词项和100万篇文档，所以其对应的词项-文档矩阵大概有5000亿个取布尔值的元素，这远远大于一台计算机内存的容量。此外，这个庞大的矩阵实际上具有高度的稀疏性，即大部分元素都是0，而只有极少部分元素为1。
  
• 也就是说对于词项个数和文档规模很大的情况，构造出的关联矩阵是高度稀疏的。这时，只记录原始矩阵中1的位置的表示方法比词项-文档关联矩阵更好。因此，引出了倒排索引。

📚倒排索引

🐇关于索引

• 索引（Index）由词项词典（Dictionary）和一个全体倒排记录表（Postings）组成。图 1-3 中的词典按照字母顺序进行排序，而倒排记录表则按照文档ID号进行排序。
  

🐇建立索引

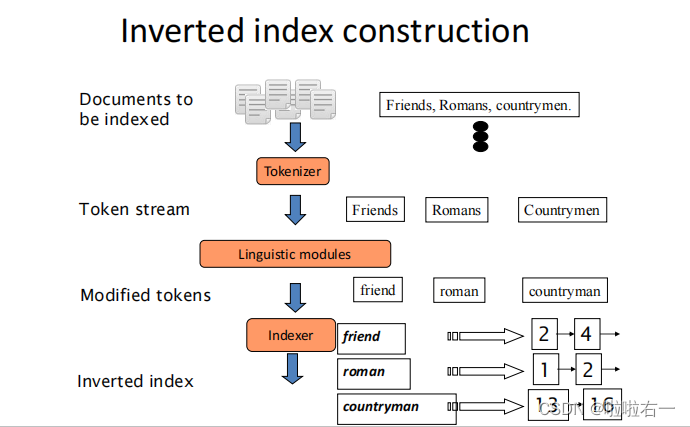
• 预处理：词语切分、词项归一化、词干还原与词形合并、去除停用词
  

• 构建倒排索引

  • 给每篇文章的所有词项加上文档ID。
    

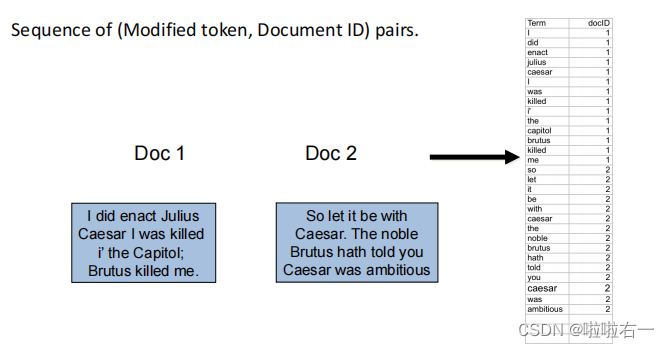
  • 按照字母顺序排序。
    

  • 将同一词项合并，并将词项和文档ID分开存储。
    

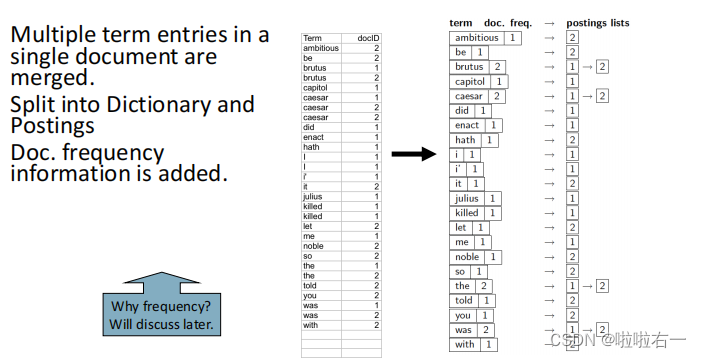
• 在字典的每个词项中还可以存储其他信息，如文档频率。

• 每个倒排记录表存储了词项出现的文档列表，还可以存储词项频率、词项在文档中出现的位置。

🐇基于倒排索引的布尔查询处理

求两个倒排记录表交集的合并算法：

• 我们对每个有序列表都维护一个位置指针，并让两个指针同时在两个列表中后移。
• 该算法对于倒排记录表集（即待合并的两个倒排记录表）的大小而言是线性的。每一步我们都比较两个位置指针所指向的文档 ID，如果两者一样，则将该 ID 输出到结果表中，然后同时将两个指针后移一位。
• 如果两个文档 ID不同，则将较小的 ID 所对应的指针后移。
• 假设两个倒排记录表的大小分别是 x 和 y，那么上述求交集的过程需要 $O(x+y)$次操作，也即查询的时间复杂度为$\Theta (N)$，其中 N 是文档集合中文档的数目。
  

• 和线性扫描相比，这种索引方法并没有带来Θ意义上时间复杂度的提高，而最多只是一个常数级别的变化。
• 但是，实际当中这个常数很大。

🐇查询优化

• 对每个词项，我们必须取出其对应的倒排记录表，然后将它们合并。
• 一个启发式的想法是，按照词项的文档频率（也就是倒排记录表的长度）从小到大依次进行处理，如果我们先合并两个最短的倒排记录表，那么所有中间结果的大小都不会超过最短的倒排记录表（这是因为多个集合的交集元素个数肯定不大于其中任何一个集合的元素个数） ，这样处理所需要的工作量很可能最少。

---

• 布尔查询适合精确查询。

📚字典数据结构

Two main choices——Hashtables、Trees

🐇哈希表

数据结构 | 第十章：散列表 | 字典 | 线性探查 | 链式散列 | LZW编码

🐇各种树

数据结构可视化网站

数据结构 | 第十一章：二叉树和其他树 | 【前序遍历】【中序遍历】【后序遍历】【层次遍历】 | 并查集
数据结构 | 第十二章：优先级队列 | 堆 | 左高树 | 堆排序 | 霍夫曼编码
数据结构 | 第十四章：搜索树 | 二叉搜索树的查找、插入、删除
数据结构 | 第十五章：平衡搜索树——AVL树 | AVL树的搜索、插入、删除
数据结构 | 第十五章：平衡搜索树——B-树 | B-树的搜索、插入、删除

---

🐇B树 vs B+树

• B树
  
  

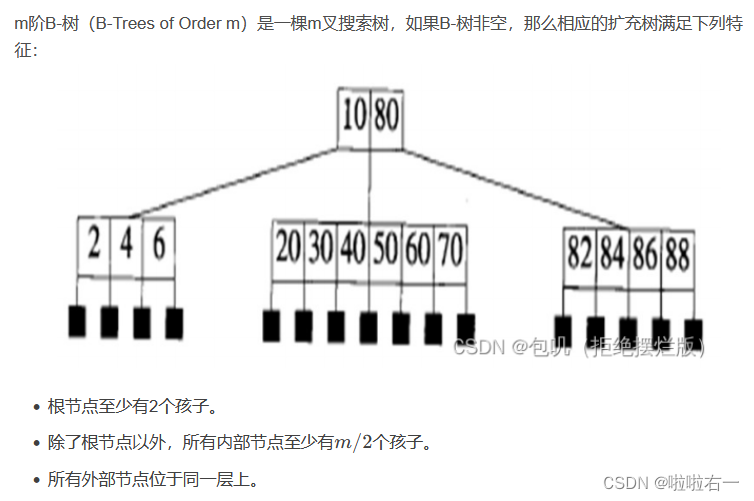
• B+树
  

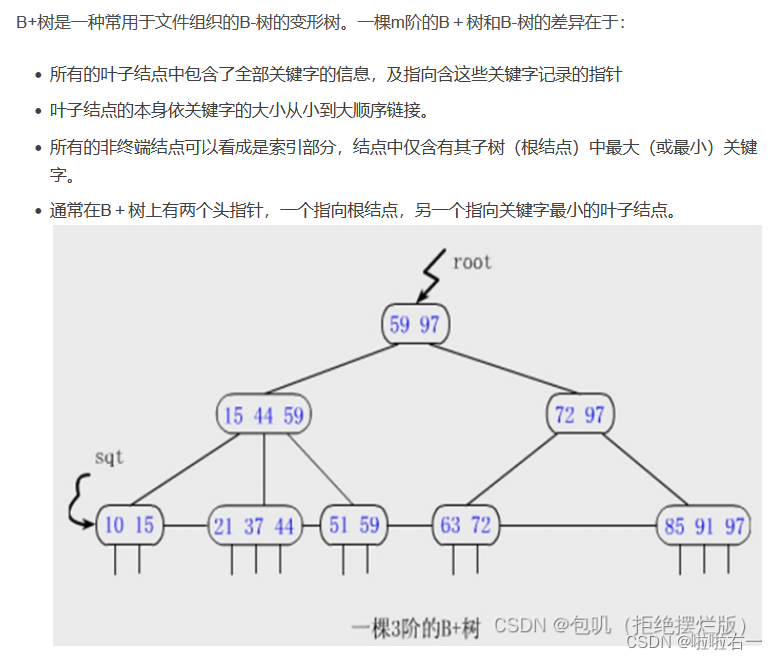
• B+树和B树相比的主要区别：
  • B+树所有关键码都在叶子节点
  • B+树的叶子节点是带有指针的，且叶节点本身按关键码从小到大顺序连接
  • 在搜索过程中，如果查询和内部节点的关键字一致，那么搜索过程不停止，而是继续向下搜索这个分支。因此，在B+树中，不管查找成功与否，每次查找都是走了一条从根到叶子结点的路径。

---

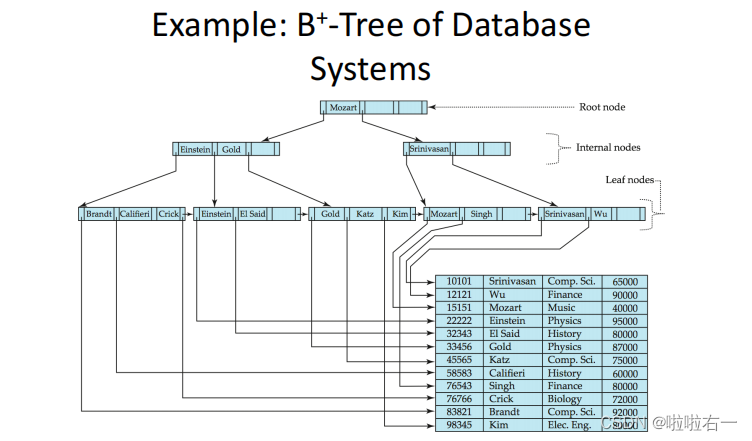
• B+树在文件系统、数据库系统当中，更有优势，更高效。
  • B+树更有利于对数据库的扫描 ，因为所有元素都在叶子节点上。
  • B+树的查询效率更加稳定 ，B树最后就是要找到叶子节点，每次查找都是走了一条从根到叶子结点的路径。
  • B+树没有像B树一样，把一些关键码每层都放一部分，之间存在互相之间的关系。在考虑指针指向内容上，B+树没有这些要存，反而数据量大的情况的，占的空间要比B树小。
    

📚短语查询及含位置信息的倒排记录

🐇二元词索引（Biword indexes）

• 对文档中每个接续词对（Biword）看成词项，这样马上就能处理两个词构成的短语查询。
• 更长的查询可以分成多个短查询来处理。
• 比如，按照上面的方法可以将查询 stanford university palo alto分成如下的布尔查询：“stanford university” AND “university palo” AND “palo alto”。
• 可以期望该查询在实际中效果会不错，但是偶尔也会有错误的返回例子。对于该布尔查询返回的文档，我们并不知道其是否真正包含最原始的四词短语。
  

🐇位置信息索引

• 在位置信息索引（positional index）中，对于每个词项，以如下方式存储倒排记录：
  
  
• 短语查询处理
  
  
• 同样，类似的方法可以用于 k 词近邻搜索当中：employment /3 place ，这里，/k 意味着“ 从左边或右边相距在 k 个词之内” 。很显然，位置索引能够用于邻近搜索，而二元词索引则不能。

🐇混合索引机制

• 二元词索引和位置索引这两种策略可以进行有效的合并。
• 假如用户通常只查询特定的短语，如Michael Jackson，那么基于位置索引的倒排记录表合并方式效率很低。
• 一个混合策略是：对某些查询使用短语索引或只使用二元词索引，而对其他短语查询则采用位置索引。
• 短语索引所收录的那些较好的查询可以根据用户最近的访问行为日志统计得到，也就是说，它们往往是那些高频常见的查询。

📚基于跳表的倒排记录表快速合并算法

• 跳表（skip list）：在构建索引的同时在倒排记录表上建立跳表。跳表指针能够提供捷径来跳过那些不可能出现在检索结果中的记录项。
  
• 在什么位置上放置跳表指针？
  • 跳表指针越多意味着跳跃的步长越短，那么在合并过程中跳跃的可能性也更大，但同时这也意味着需要更多的指针比较次数和更多的存储空间。跳表指针越少意味着更少的指针比较次数，但同时也意味着更长的跳跃步长，也就是说意味着更少的跳跃机会。
    
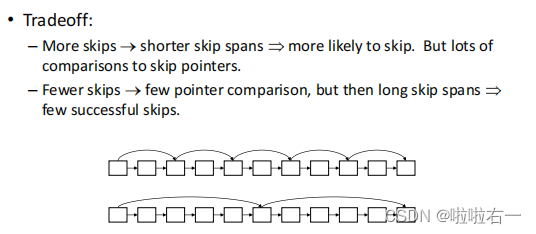
  • 放置跳表指针位置的一个简单的启发式策略：在每个 $\sqrt{P}$ 处均匀放置跳表指针，其中 $P$ 是倒排记录表的长度。
  • 这个策略在实际中效果不错，但是仍然有提高的余地，因为它并没有考虑查询词项的任何分布细节。
  • 如果索引相对固定的话，建立有效的跳表指针则比较容易。但是如果倒排记录表由于经常更新而发生变化，那么跳表指针的建立就比较困难。恶意的删除策略可能会使跳表完全失效。

---

参考博客：

• B树和B+树的区别